Вопрос №11

(ребят, смотрите опять дополнения к вопросу №4)

Вопрос №12

Гидростатическое давление столба жидкости или газа:    ,   где  .

,   тогда         =>          =>        ;

В итоге мы получаем:     −   барометрическая формула. Барометрическую формулу можно преобразовать, если воспользоваться выражением :

- распределение Больцмана во внешнем потенциальном поле. Из нее следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

Вопрос №13

Молекулы в состоянии теплового движения имеют различные скорости и скорости эти постоянно меняются.

Максвелл, исходя из законов теории вероятности решил задачу о распределении молекул по скоростям поступательного движения.

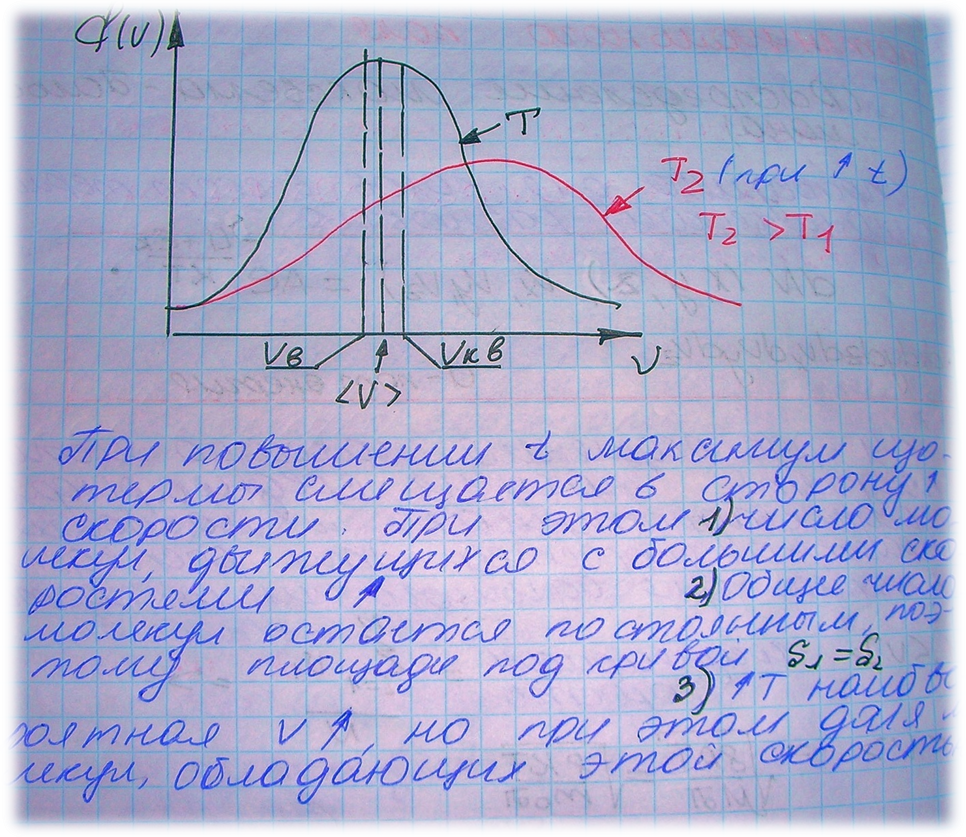
Закон позволяет определить, какое количество молекул dN от общего числа молекул N обладает скоростями от V до V + dV (при данной температуре).

При этом Максвелл предположил:

1. Все молекулы одинаковые (неразличимы);

2. Температура постоянна;

3. Отсутствует внешнее воздействие на газ.

A1 – коэффициент, который находят из условия нормировки, а под знаком экспоненты стоит кинетическая энергия молекулы, делённая на KT.

Наиболее вероятная скорость – скорость, при которой распределения молекул по скоростям максимально.

Вопрос №14

• все тела состоят из частиц: атомов, молекул и ионов;

• частицы находятся в непрерывном хаотическом движении (тепловом);

• частицы взаимодействуют друг с другом путём абсолютно упругих столкновений( Между молекулами действует сила взаимодействия, притяжения, отталкивания).

Основными доказательствами этих положений считались:

• Диффузия

• Броуновское движение

• Изменение агрегатных состояний вещества

Вывод основного уравнения мкт

Пусть имеется кубический сосуд с ребром длиной и одна частица массой в нём.

Обозначим скорость движения , тогда перед столкновением со стенкой сосуда импульс частицы равен , а после — , поэтому стенке передается импульс . Время, через которое частица сталкивается с одной и той же стенкой, равно .

Отсюда следует:

Так как давление , следовательно сила

Подставив, получим:

Преобразовав:

Так как рассматривается кубический сосуд, то

Отсюда:

.

Соответственно, и .

Таким образом, для большого числа частиц верно следующее: , аналогично для осей y и z.

Поскольку , то . Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.

Отсюда

или .

Пусть  — среднее значение кинетической энергии всех молекул, тогда:

, откуда, используя то, что , а , имеем .

Вопрос №15

,

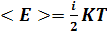– средняя энергия одной молекулы.

E = (½)KT – энергия, которая приходится на одну степень свободы.

В системе, состоящей из большого числа частиц на одну степень свободы приходится одно и то же количество частиц, равное (½)KT.

Молек.	Поступательное	Вращательное	Колеб.	i
Одноатомн.	3	-	-	3
Двухатомн. Жестк.	3	2	-	5
Двухатомн. Упруг.	3	2	1	6
Трёхатомн. Жестк.	3	3	-	6

Недостатки классической теории теплоемкостей идеального газа:

1. Согласно КТТ теплоёмкость всех двухатомных газов должна быть одинаковой. Но опыт показывает, что это не так.

2. Классическая теория теплоёмкости приходит к выводу, что теплоёмкость не зависит от температуры. Но на самом деле С сильно понижается (стремится к нулю) с понижением Т, и повышается с повышением Т.

3. Для многоатомных молекул КТТ даёт заниженное значение теплоёмкости по сравнению с экспериментом при высоких и средних температур.

Причина этих разногласий заключается в ограниченной пригодности закона . Даже введение колебательных степеней свободы не убирают разногласия. Все эти расхождения устраняются в квантовой теории теплоёмкости.