Вопрос №5

А 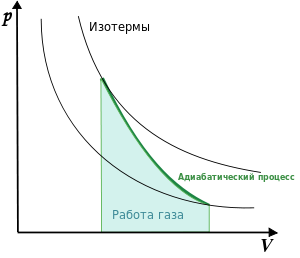диабата идёт круче, чем изотерма, потому что в адиабатическом процессе меняются всё три параметра.

 — давление газа;  — объём.

Вопрос №6

См вопрос №4 (дополнения).

Вопрос №7

Теплоёмкость – величина, которая зависит от вида процесса.

Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло.

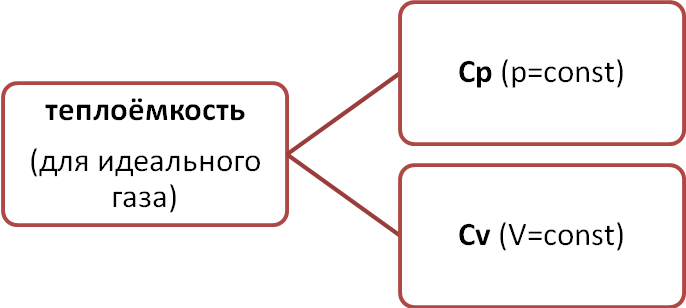
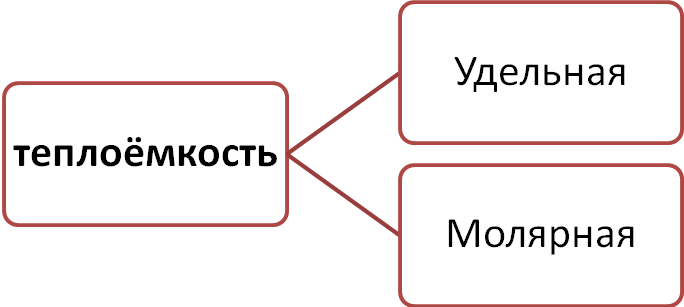
Удельная теплоёмкость (Удельная теплота нагревания на один градус, С уд.) вещества - количество тепловой энергии, необходимой для повышения температуры одного килограмма вещества на один градус. (Дж/(кг ·К)).

Формула расчёта удельной теплоёмкости: .,

где  — удельная теплоёмкость,

 — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),

 — масса нагреваемого (охлаждающегося) вещества,

 — разность конечной и начальной температур вещества.

Молярная теплоёмкость (С_μ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. (Дж/(моль·К)).

Формула расчёта молярной теплоёмкости: .

Удельная и молярная теплоемкости связаны соотношением: , где

М — молярная масса (масса одного моля вещества).

Чаще всего работаем с молярной теплоёмкостью!

Вопрос №8

Сp – теплоёмкость вещества при постоянном внешнем давлении.

Cv – теплоёмкость вещества при постоянном внешнем объёме.

Для газа Cp>Cv, так как в случае постоянного давления тепло идёт как нагревание газа, так и на совершение работы расширяющимся газом против внешних сил, а в случае постоянного объёма тепло идёт только на нагревание газа.

Из кинетической теории известно, что

Вопрос №9

Q = dU

*dT = (i/2)* *R*dT

= (i/2)*R

= + R = (i/2) + R = ((i+2)/2)*R

= ((i+2)/2)*R

= (i/2)*R

Вопрос №10

(лучше конечно, ответ на этот вопрос посмотреть в 81 методичке на странице 83)

Цель работы: изучение различных изопроцессов протекающих в газах, экспериментальное определение СP/СV для воздуха.

Приборы и принадлежности: прибор Клемана – Дезорма манометр, насос, секундомер.

Теоретическое введение: Теплоёмкостью какого-либо тела Сm называется величина, численно равная количеству теплоты Q, которое требуется сообщить этому телу для повышения его температуры на 1 кельвин.

Удельной теплоёмкостью Суд. называется теплоёмкость единицы массы вещества. Молярной теплоёмкостью вещества называется С – называется теплоёмкость вещества взятого в количестве одного моля. Из определения С следует, что С = Суд, где  - молярная масса вещества.

Согласно основному закону термодинамики количество теплоты Q, переданное газу, затрачивается на увеличение его внутренней энергии dU и на совершении газом работы A.

Q = dU + A;

Внутренняя энергия системы является функцией её состояния, а количество теплоты и работа являются функцией процесса.

Из определения теплоёмкости имеем формулу:

Теплоёмкость С так же является функцией процесса так, как передаваемая газу количество теплоты Q способа нагрева газа.

Состояние газа, как термодинамической системы определяется следующими параметрами: давлением p, объёмом V и температурой T. Связь данных параметров определяется Уравнением состояния идеального газа – уравнением Менделеева-Клайперона:

pV = RT.

Где R – универсальная газовая постоянная.

Процессы, протекающие в газе при неизменном значении одного из термодинамических параметров его состояния, называются изопроцессами.

Изохорный процесс протекает при V = const. Уравнение изохоры имеет вид: const (закон Шарля). В данном случае dV = 0, A = pdV = 0. Тогда из уравнения (2) получаем:

Изобарный процесс протекает при p = const. Уравнение изобары имеет вид: const (закон Гей-Люссака). Теперь уравнения (2) имеет вид:

Тогда из уравнения (3) получаем:

При p = const получим pdV = RdT, подставим его в (5) и учтя выражение (4) имеем следующее выражение (уравнение Майера):

Cp = CV + R;

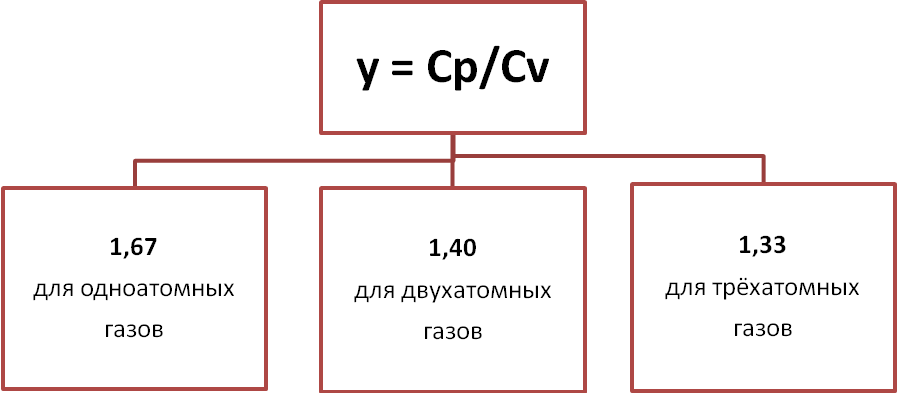
Молярные теплоёмкости Cp и CV идеального газа зависят от числа степеней свободы i его молекулы. Атом одноатомного газа имеет i = 3 (X, Y, Z). Молекулы 2-ух атомного газа имеют i = 5 (3 – степени свободы поступательного движения и 2 вращательного). Молекулы состоящие из 3-ёх и более атомов имеют 6 степеней свободы (i = 6).

При высоких температурах кроме поступательного и вращательного движения молекулы (атома) необходимо учитывать и её колебательное движение (около положения равновесия) т. е. У двухатомной молекулы – 1 колебательная степень свободы, у многоатомных молекул 3N – 6, где N – число атомов в молекуле. На каждую степень свободы приходится примерно одинаковое количество кинетической энергии, равное kT/2, где k – постоянная Стефана – Больцмана. Тогда внутренняя энергия одного моля идеального газа равна:

,

где i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы.

Из уравнений (4), (7) и (8) следует, что:

, .

Изотермический процесс протекает при T = const. Уравнение изотермы имеет вид: const (закон Бойля - Мариотта). Следовательно:

dT = 0, dU = 0, Q =A.

Адиабатный процесс протекает при Q = 0. Следовательно: dU + A = 0. От сюда получаем выражение:

A = -dU.

Из данного выражения получаем уравнение адиабаты:

pdV = -CVdV (уравнение Пуассона).

Из вышеприведённых уравнений (6), (7) и (11) следует, что:

,

где

.

Интегрируя и потенцируя (12), получим уравнение Пуассона:

pV = const.

В данной работе требуется определить СP/СV = , для этого в течение всего эксперимента газ (в установке) последовательно будет проходить через 3 состояния (рис. 1): 1-2 адиабатное расширение, 2-3 изохорный процесс.

Для адиабатного перехода 1-2 справедливо уравнение Пуассона:

Первое и третье состояние газа принадлежит одной той же изотерме. Применяя к ним закон Бойля – Мариотта, получаем:

p1V1 = p3V2;

Из уравнений (14) и (15) следует, что

.

Прологарифмировав это выражение получим:

Давление воздуха в баллоне в первом состоянии определяется, как

p1 = p2 + gH,

где  - плотность вещества; g – ускорение свободного падения; H – разность уровней жидкости в трубках манометра при измерении p1.

Давление воздуха в баллоне в третьем состоянии определяется, как

p3 = p2 + gh,

где h – разность уровней жидкости в трубках манометра при измерении p3.

Так, как давление p1 и p3 примерно равно атмосферному давлению p2, то формулу (17) можно упростить, использую следующее равенство:

, которое выполняется для всех x << 1. Тогда: