Розділ 3
Графічно розв’язати системи.
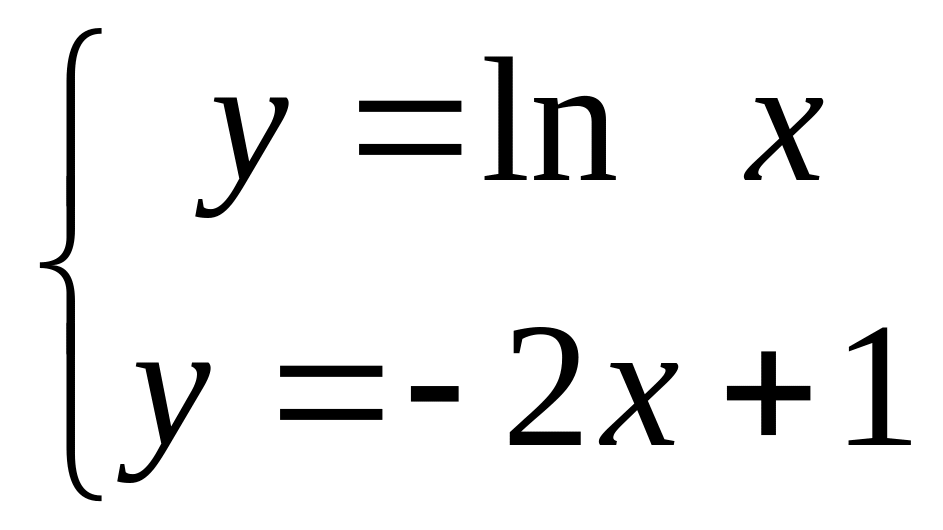 в діапазоні х
[0,2; 3] з кроком
=0,2.
в діапазоні х
[0,2; 3] з кроком
=0,2.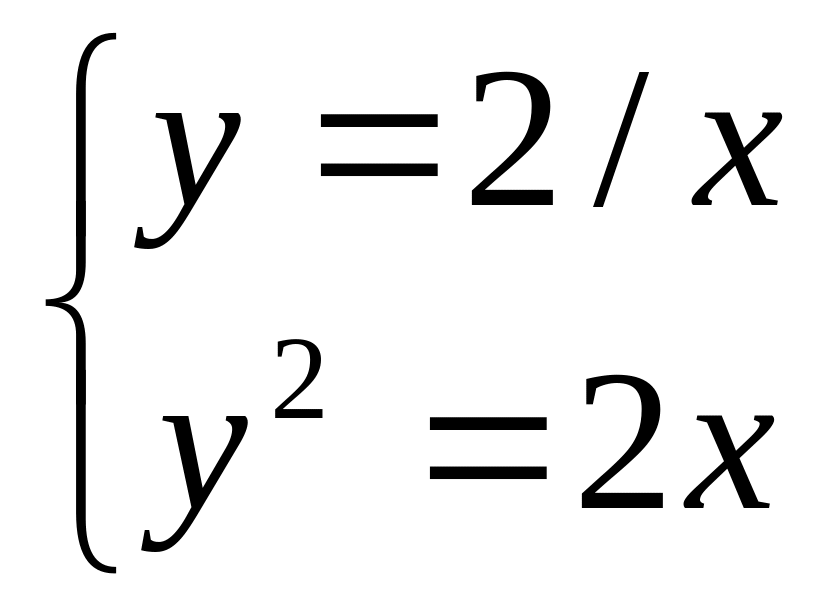 в діапазоні х
[0,2; 3] з кроком
=0,2.
в діапазоні х
[0,2; 3] з кроком
=0,2.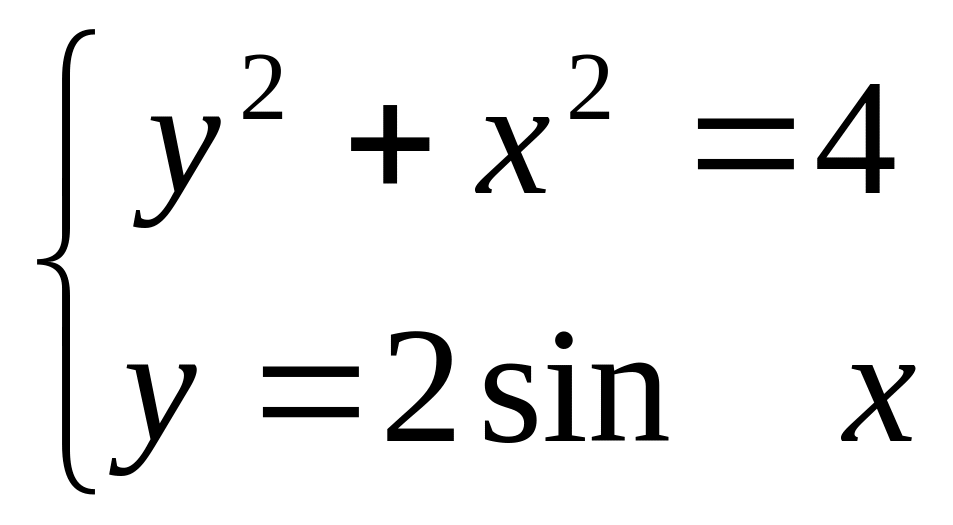 в діапазоні х
[0; 3] з кроком
=0,2.
в діапазоні х
[0; 3] з кроком
=0,2.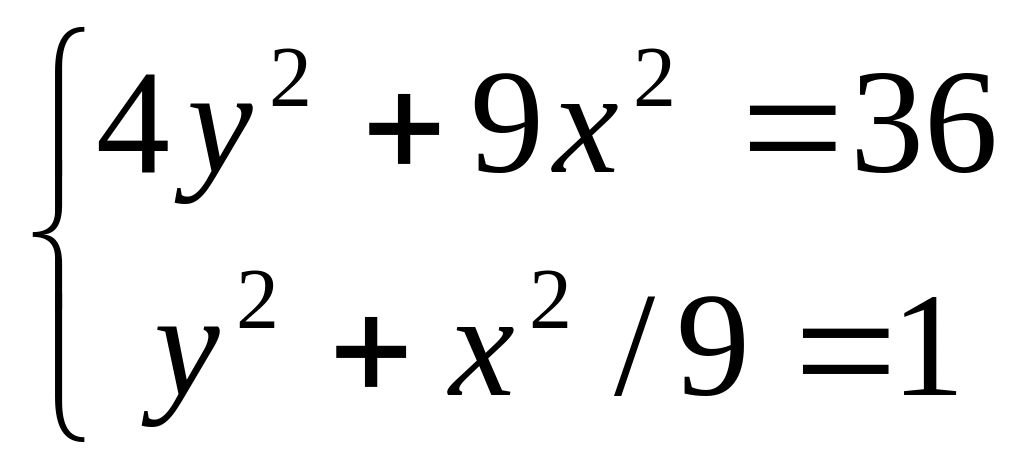 в діапазоні х
[0; 3] з кроком
=0,2.
в діапазоні х
[0; 3] з кроком
=0,2.
Розділ 4
Побудувати площину паралельно площині Оху що перетинатиме вісь Оz в точці М (0,0,2). Діапазони коливання змінних х та у: х [0; 6] з кроком =0,5, y [0; 6] з кроком =1.
Побудувати площину з відрізками а=3, b=2 i c= 1 на координатних осях. Діапазони коливання змінних х та у: х [-1; 4] з кроком =0,5, y [-1; 3] з кроком =1.
Побудувати площину, що проходить через точки М1 (3,3,1), М2 (2,3,2), М3 (1,1,3). Діапазони коливання змінних х та у: х [-1; 4] з кроком =0,5, y [-1; 3] з кроком =1.
Побудувати верхню частину еліпсоїда
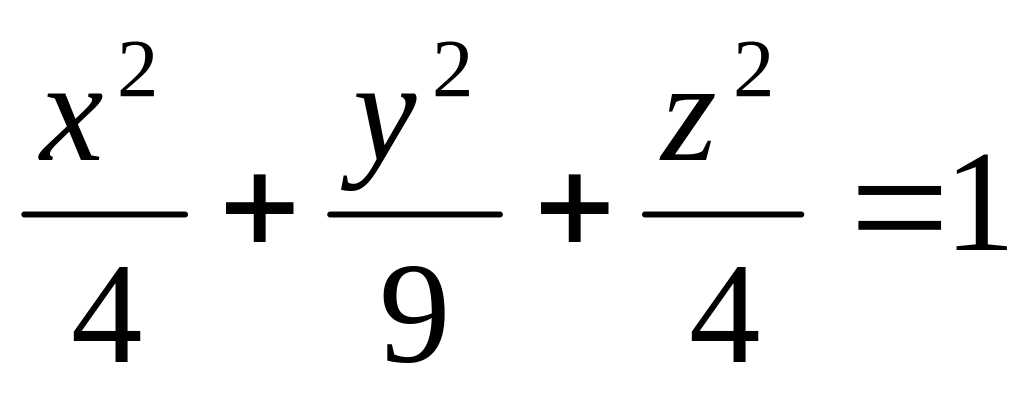 .
Діапазони коливання
змінних х
та у: х
[-2; 2] з кроком
=0,5,
y
[-3; 3] з кроком
=1.
.
Діапазони коливання
змінних х
та у: х
[-2; 2] з кроком
=0,5,
y
[-3; 3] з кроком
=1.Побудувати верхню частину однополостного гіперболоїда . Діапазони коливання змінних х та у: х [-3; 3] з кроком =0,5, y [-4; 4] з кроком =1.
Побудувати еліптичний параболоїд:
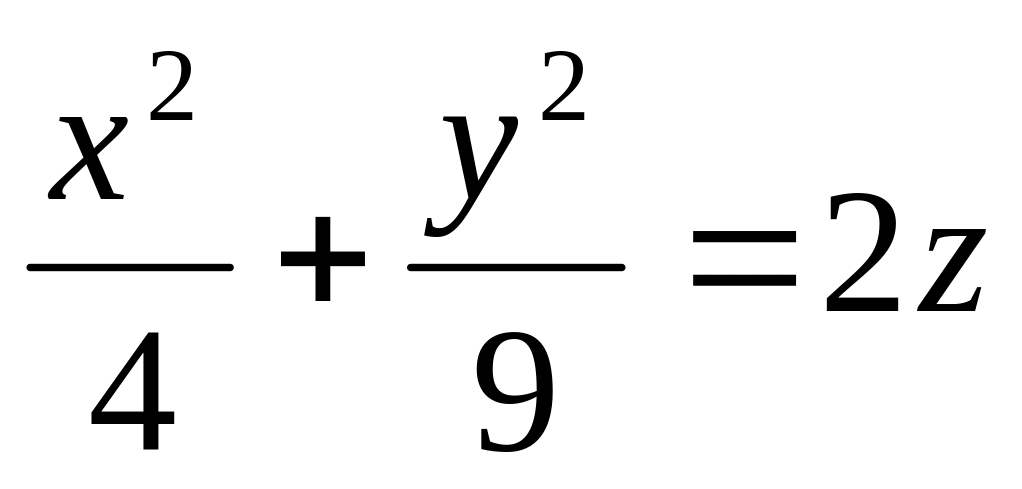 .
Діапазони коливання
змінних х
та у: х
[-2; 2] з кроком
=0,5,
y
[-3; 3] з кроком
=1.
.
Діапазони коливання
змінних х
та у: х
[-2; 2] з кроком
=0,5,
y
[-3; 3] з кроком
=1.Побудувати верхню частину конуса
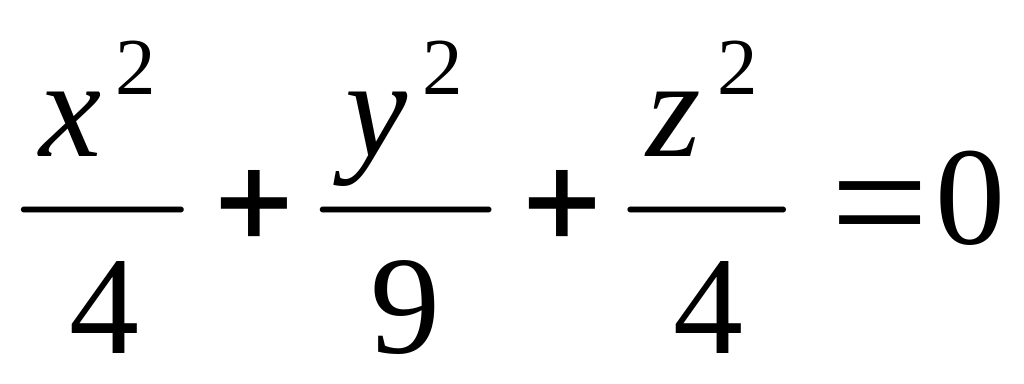 .
Діапазони коливання
змінних х
та у: х
[-2; 2] з кроком
=0,5,
y
[-3; 3] з кроком
=1.
.
Діапазони коливання
змінних х
та у: х
[-2; 2] з кроком
=0,5,
y
[-3; 3] з кроком
=1.
Розділ 5
Знайдіть добуток матриць
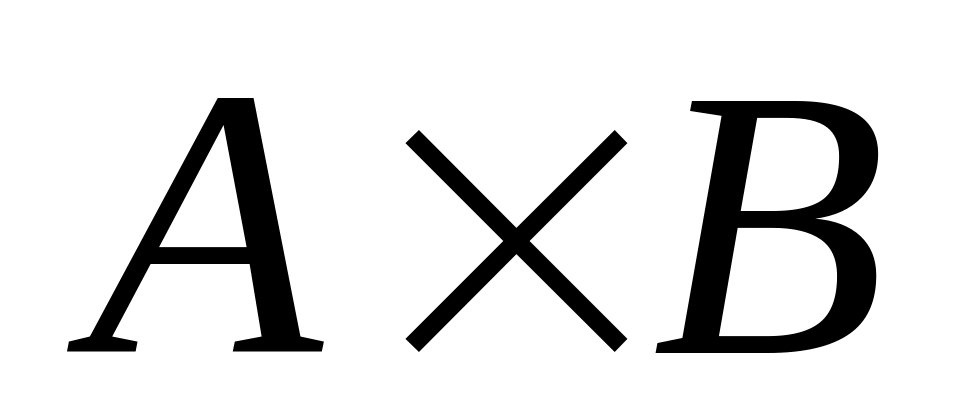 ,
де
,
де
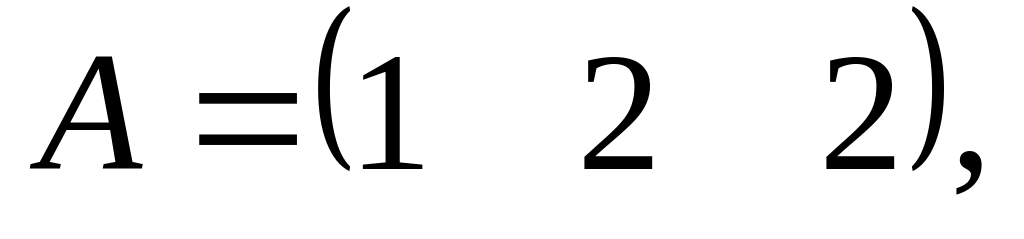
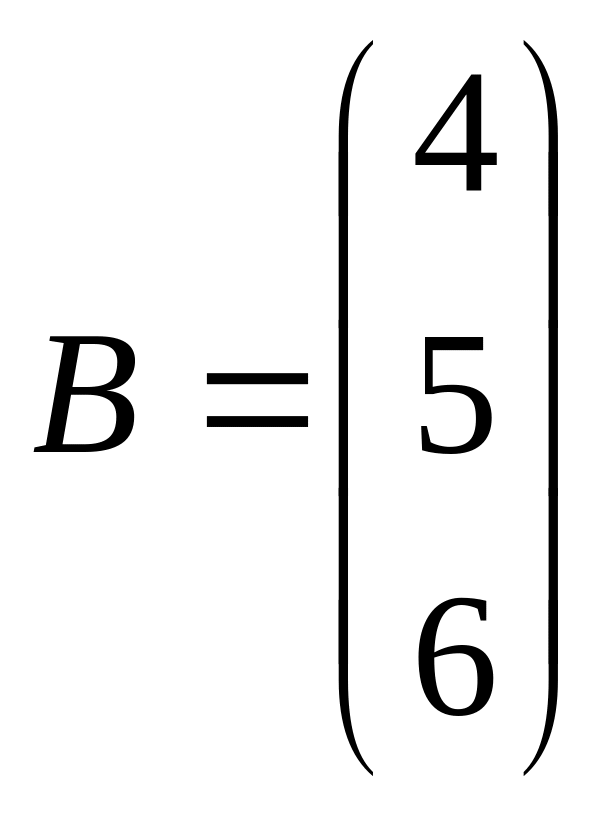 .
Знайдіть добуток матриць
.
Знайдіть добуток матриць
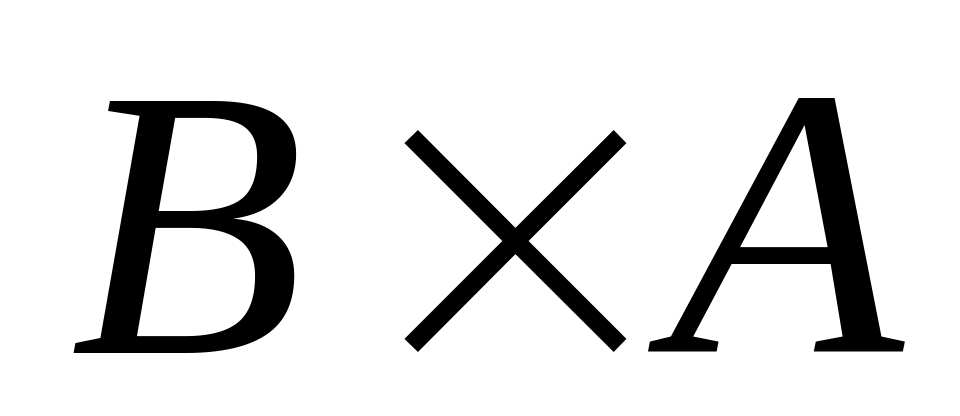 .
Знайдіть визначник матриці
.
.
Знайдіть визначник матриці
.Знайдіть добуток матриць
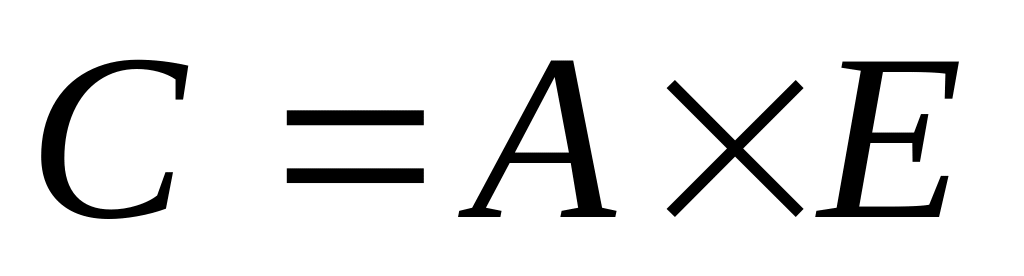 ,
де
,
де
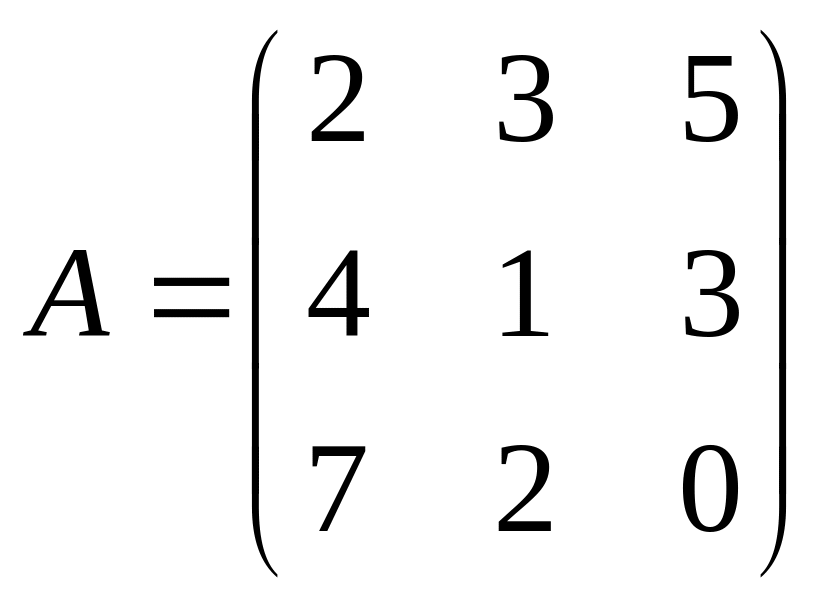
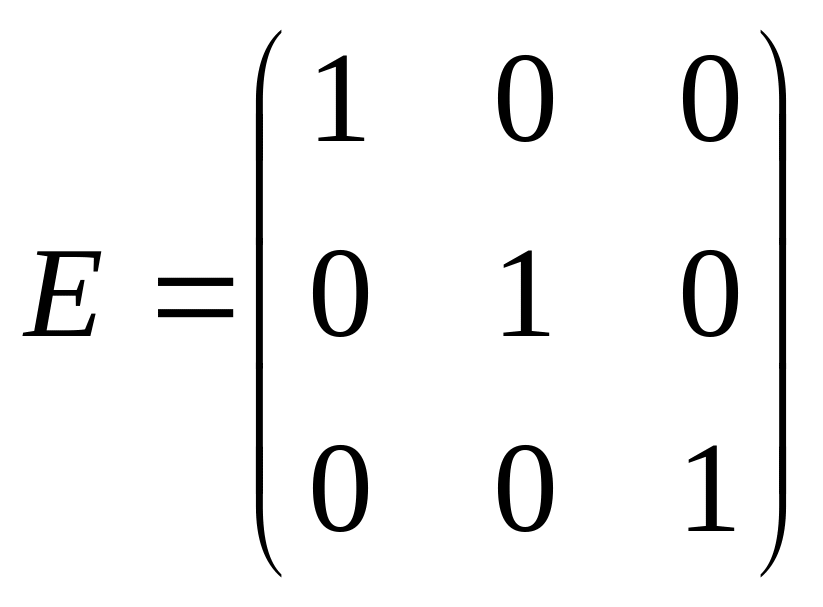
Знайдіть матрицю, обернену даній:
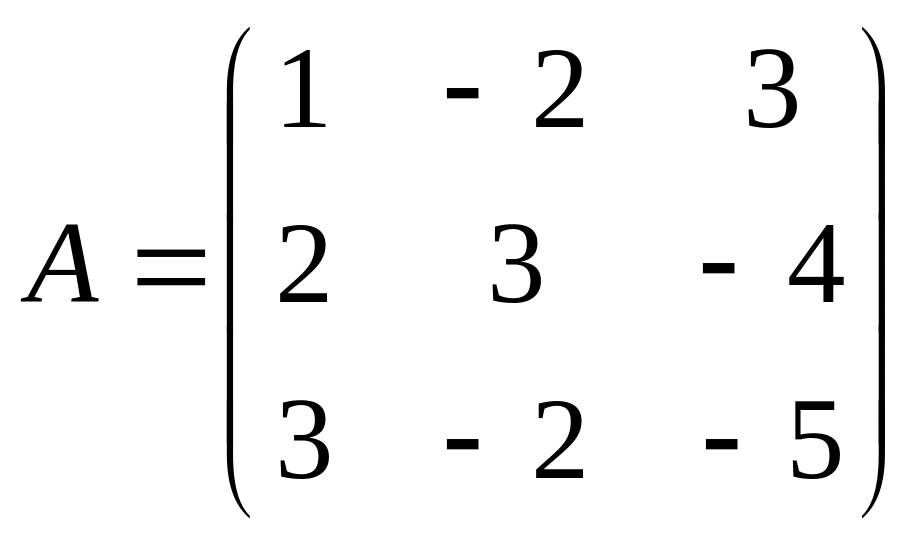
Скориставшись визначенням оберненої матриці
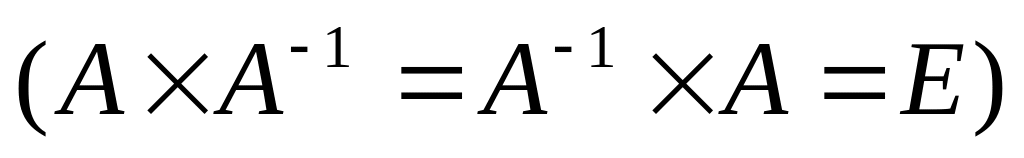 перевірте чи правильно розв’язана
матриця у вправі 5: для цього знайдіть
добуток матриці А
у вправі 5 на обернену матрицю. Аналогічним
способом перевірте, що
перевірте чи правильно розв’язана
матриця у вправі 5: для цього знайдіть
добуток матриці А
у вправі 5 на обернену матрицю. Аналогічним
способом перевірте, що
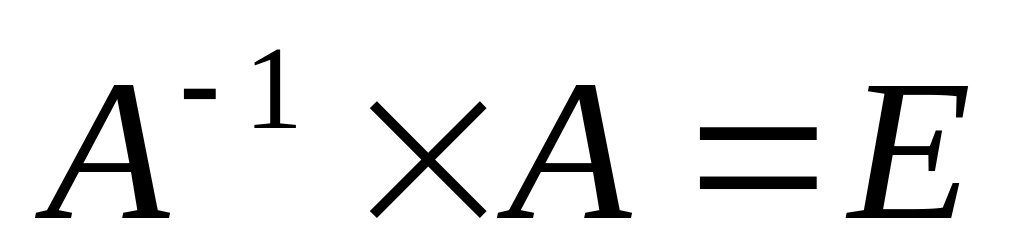 .
.Підприємство випускає продукцію трьох видів Р1, Р2, Р3 та використовує сировину двох типів S1 та S2. Норма витрат сировини характеризується матрицею:
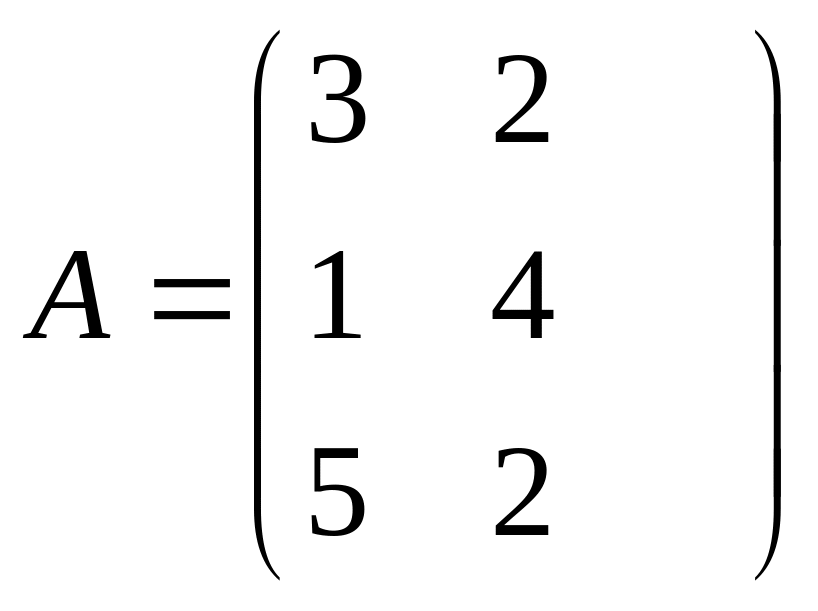
де кожен елемент показує, скільки одиниць сировини j-го типу витрачається на виробництво одиниці продукції. Вартість одиниці кожного типу сировини задана матрицею-стовпцем
![]() .
.
Визначити вартість витрат сировини на одиницю продукції.
Які із заданих матриць можна перемножити? Знайдіть їх добутки. ;
![]() ;
;
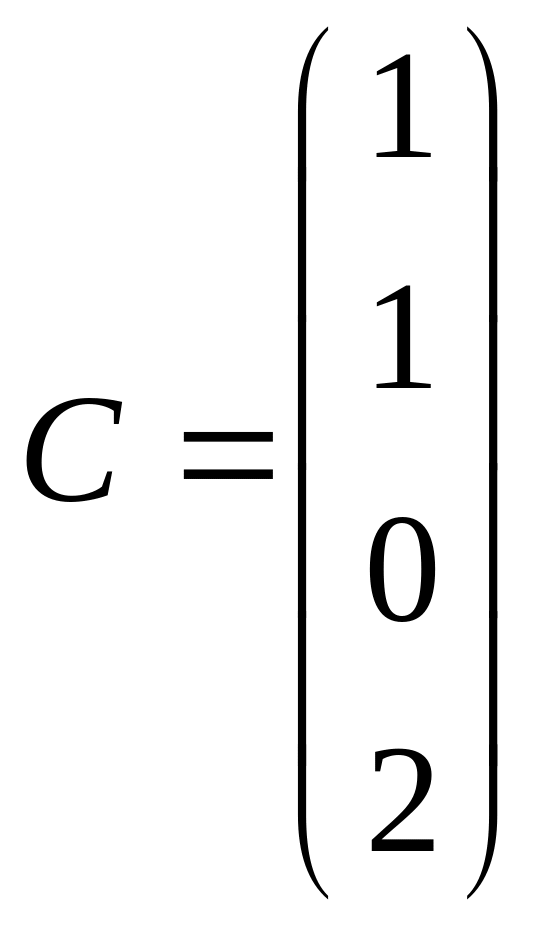 ;
;
![]() .
.
Обчисліть
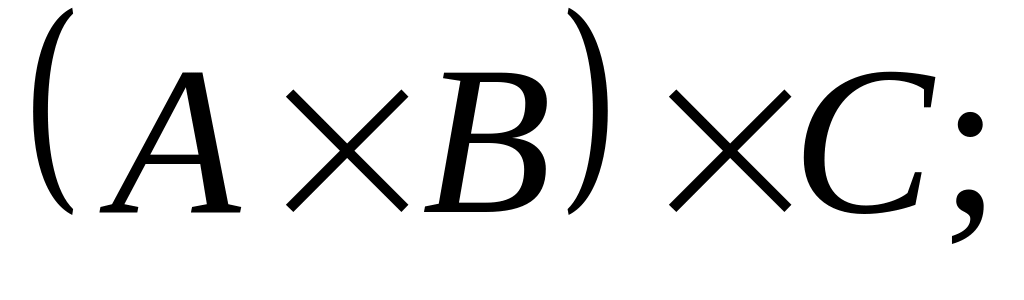
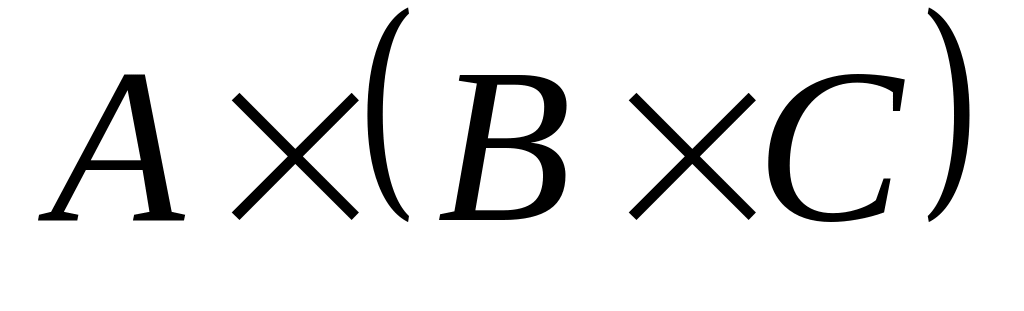 .
.
![]() ;
;
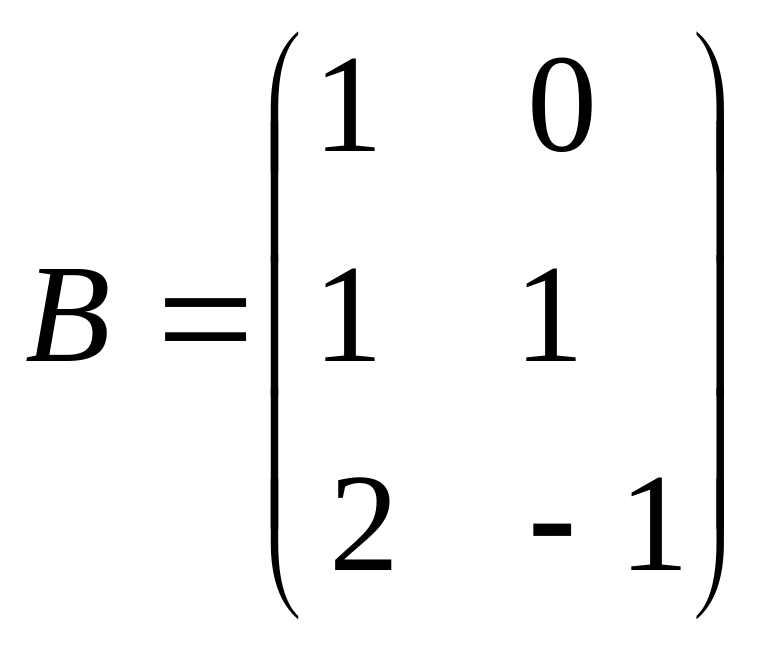 ;
;
![]()
Підтвердіть, що для вказаних матриць справджується твердження
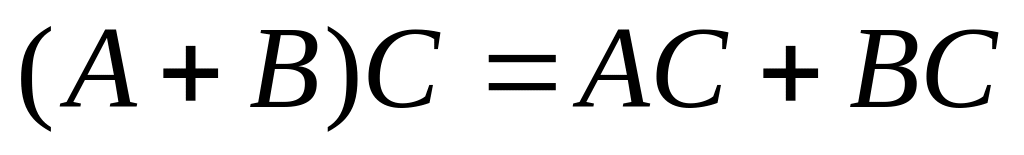 .
.
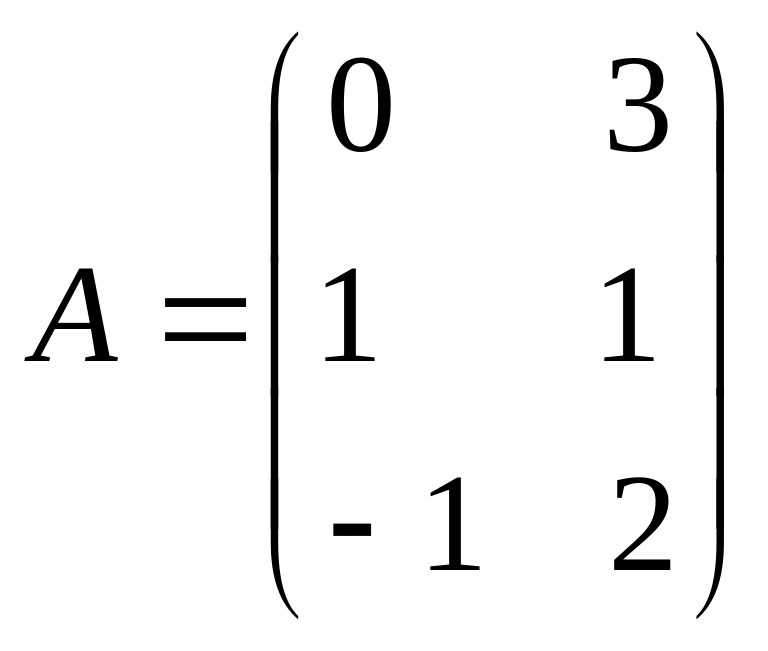 ;
;
.
;
;
.
Обчисліть
1)
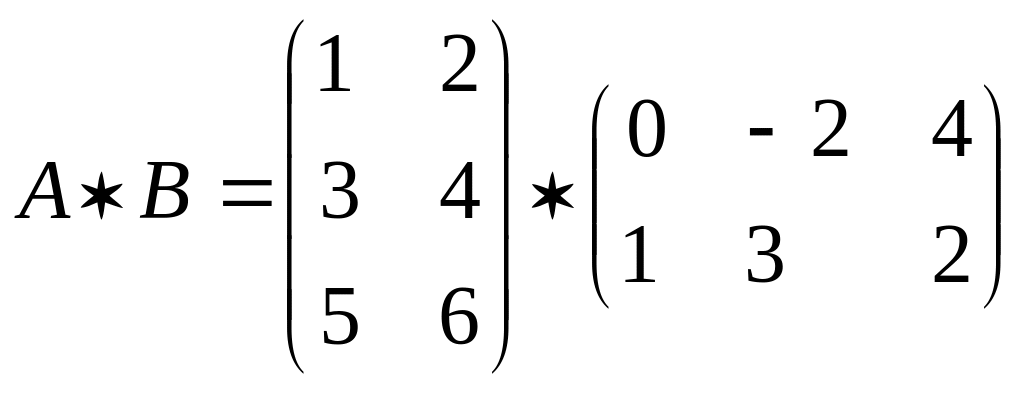
2)
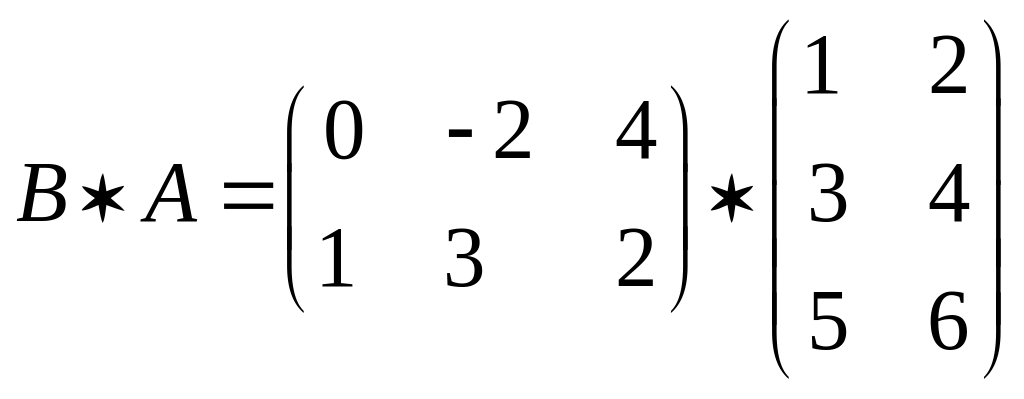 .
.
Яку властивість множення матриць демонструє даний приклад?
Знайдіть матриці, обернені даним:
1)
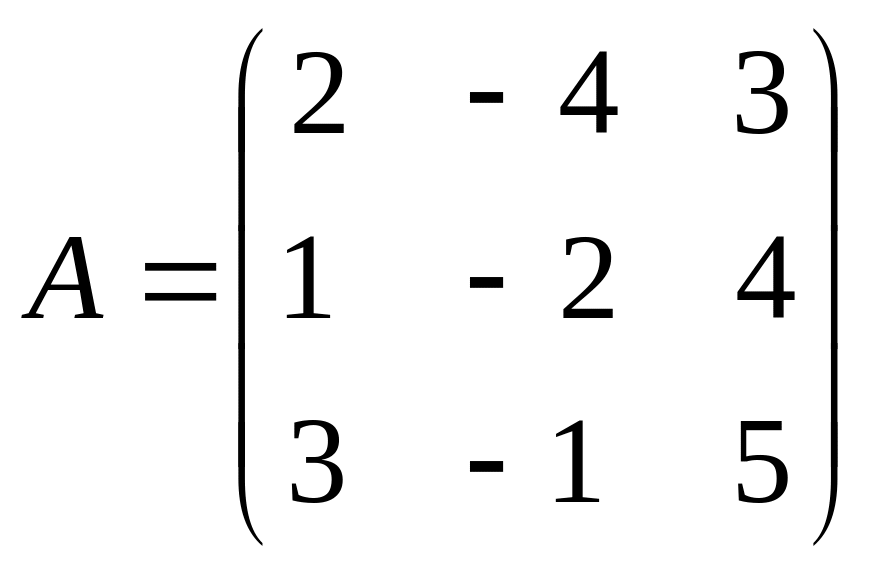 ;
;
2)
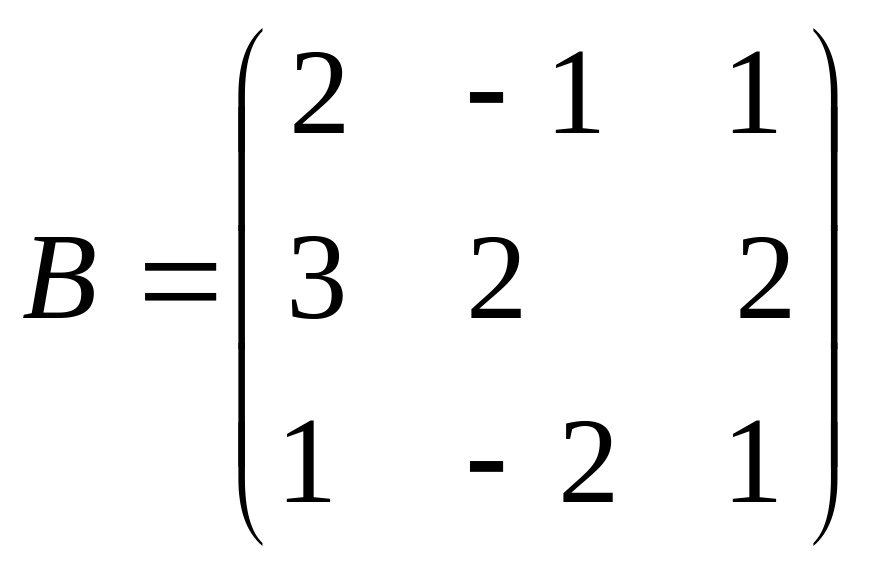 ;
;
3)
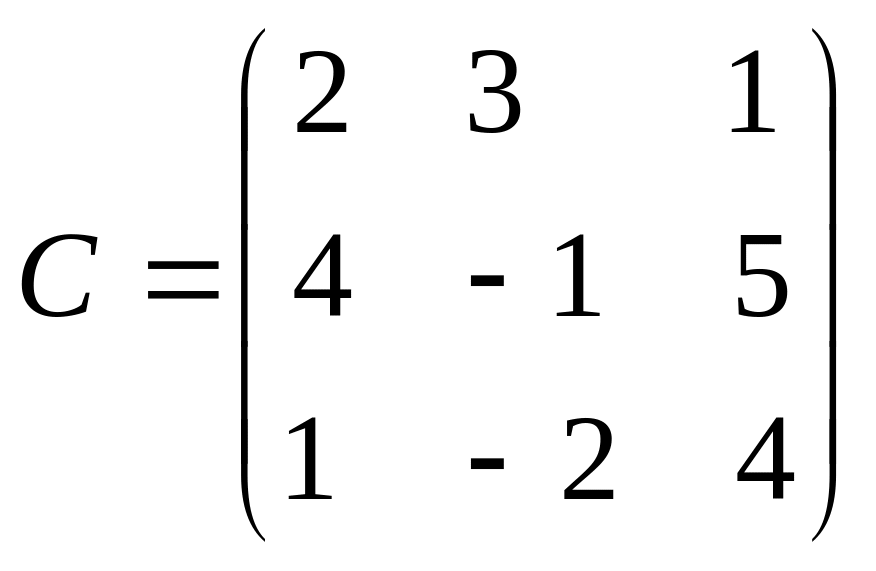 .
.
Розв’яжіть систему рівнянь:
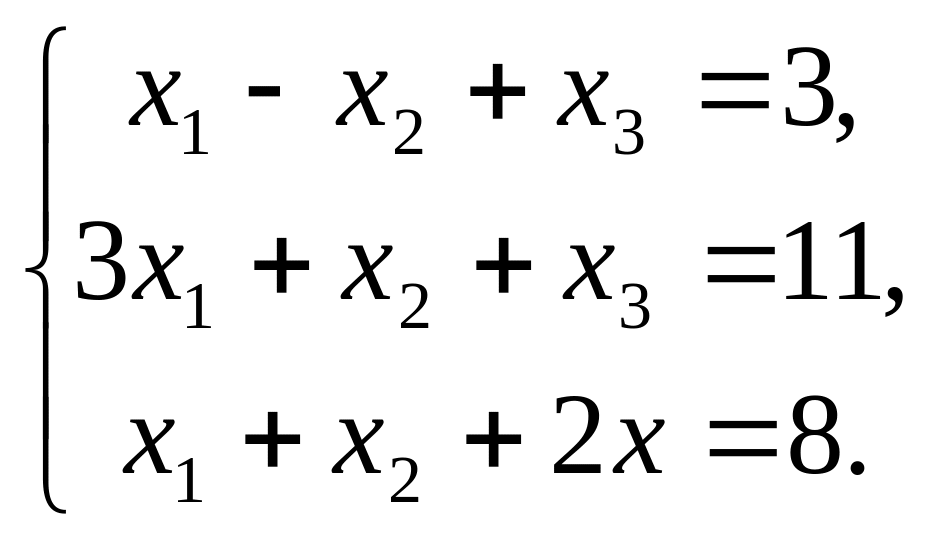
Розв’яжіть систему рівнянь:
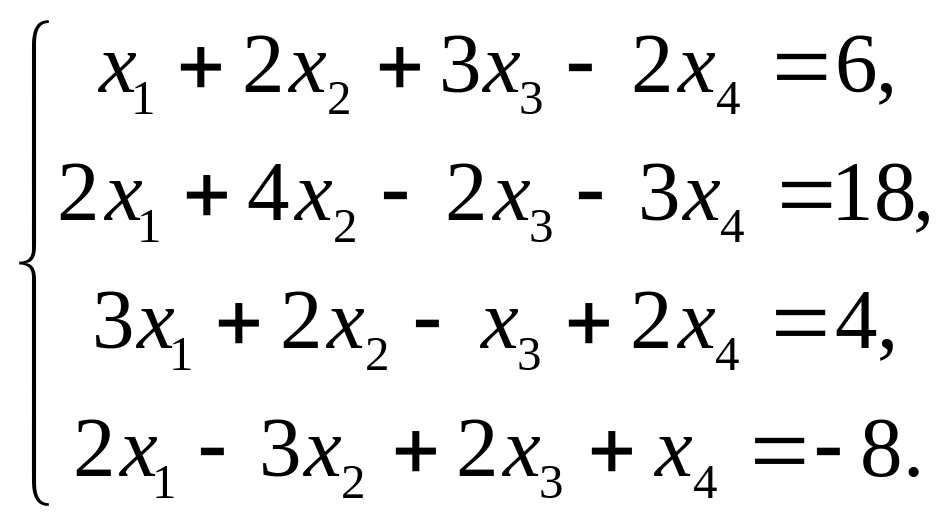
Розв’яжіть систему рівнянь:
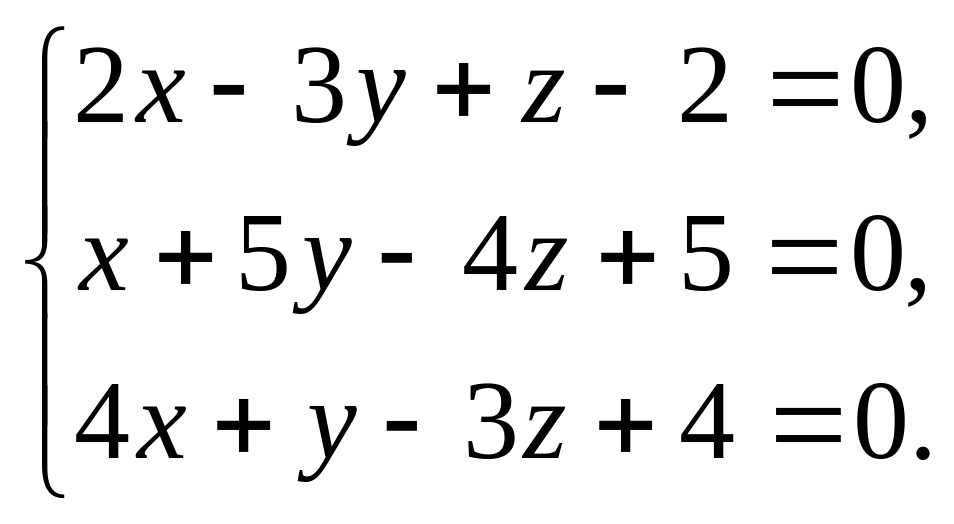
Розв’яжіть систему рівнянь:
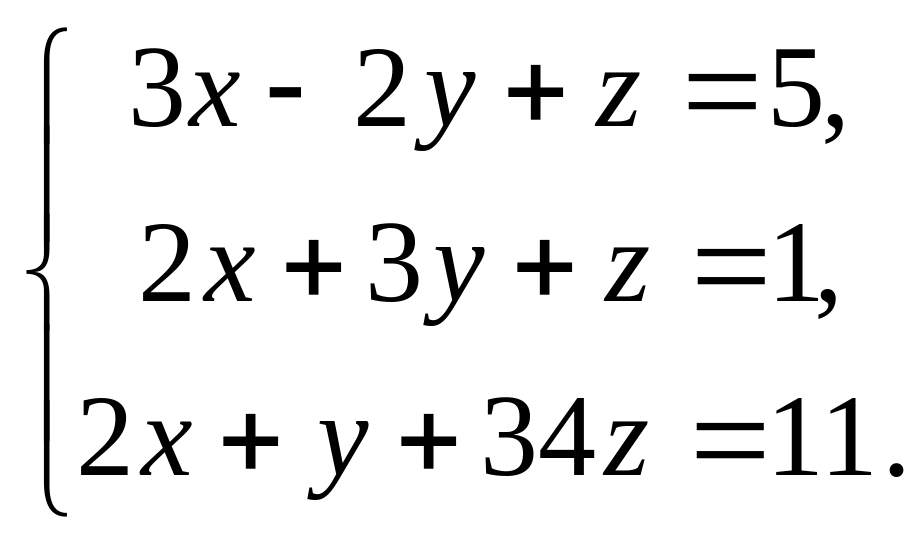
Розв’яжіть систему рівнянь:
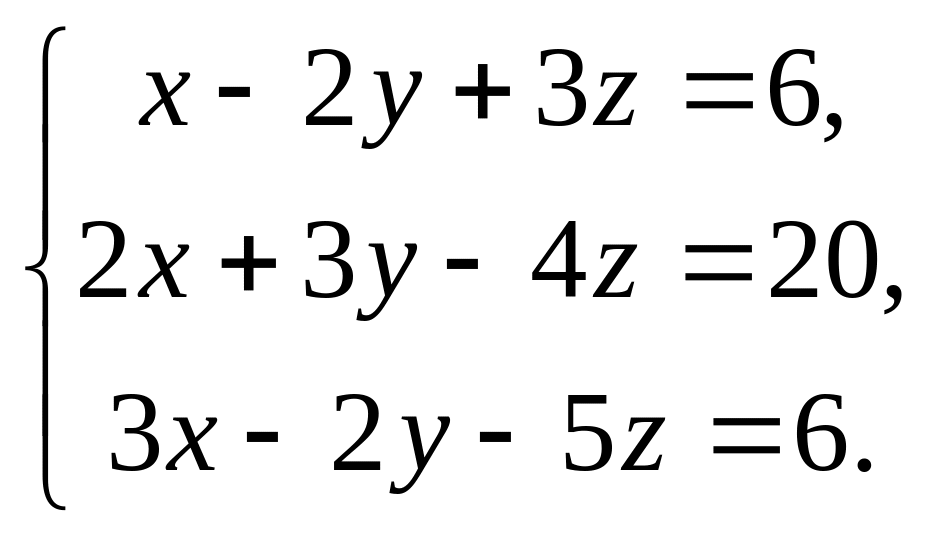
Розв’яжіть систему рівнянь:
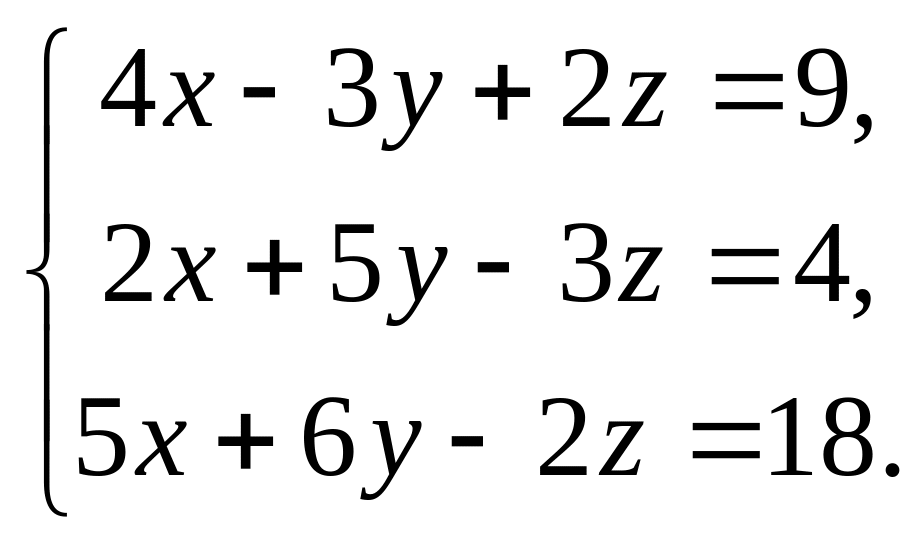
Розв’яжіть систему рівнянь:
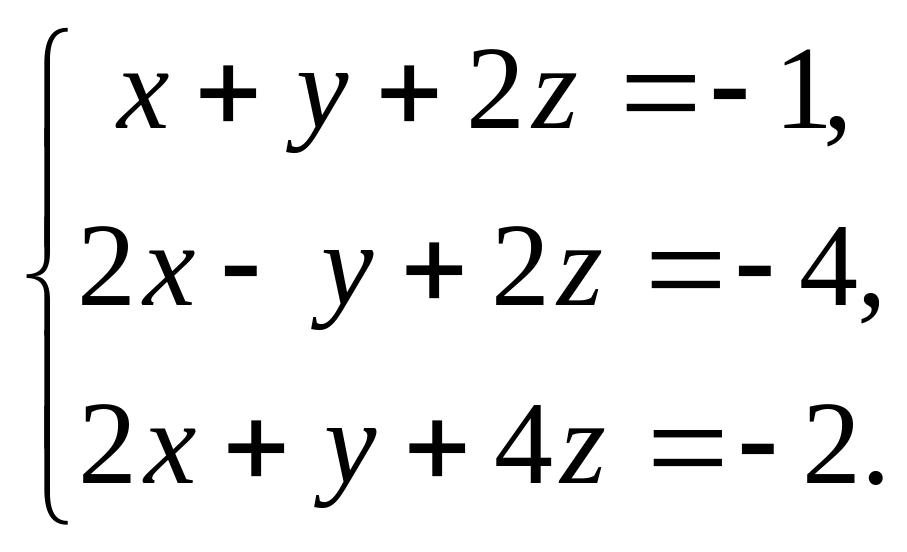
Розв’яжіть систему рівнянь:
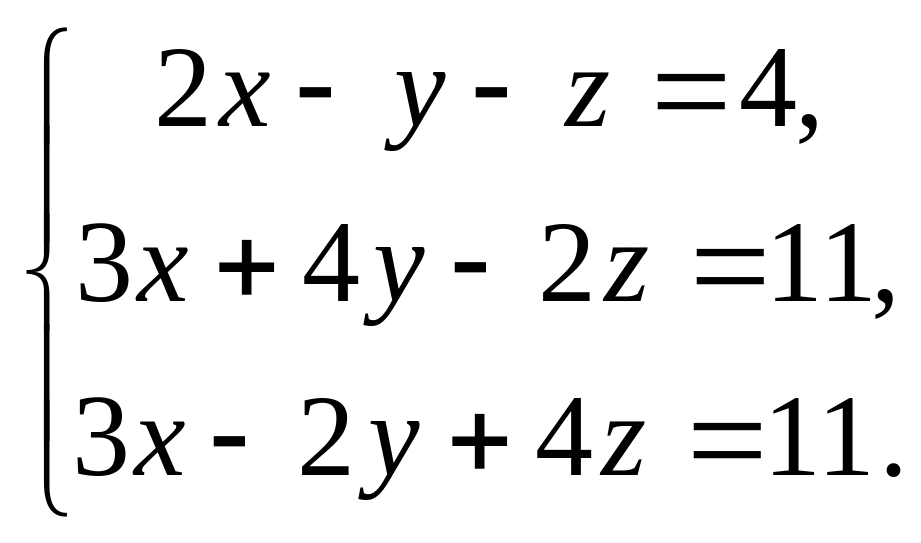
Розв’яжіть систему рівнянь:
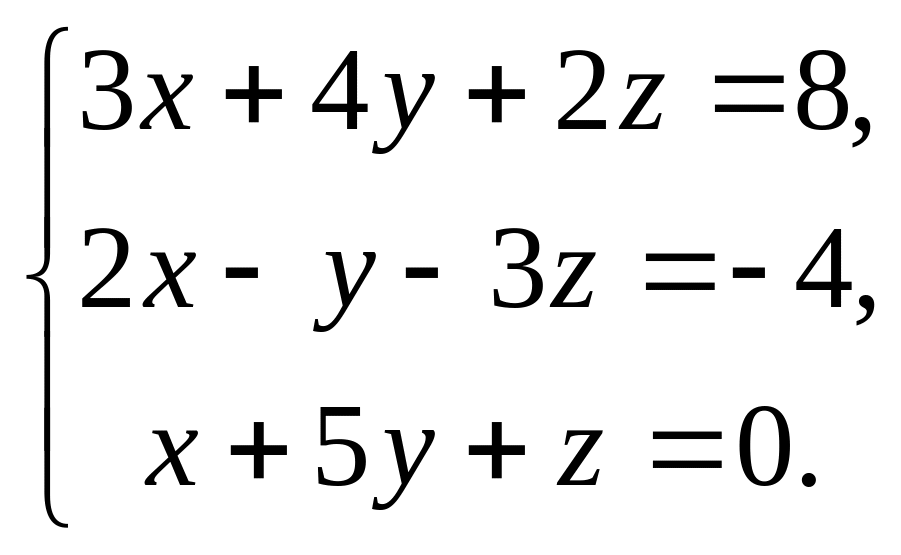
Розв’яжіть систему рівнянь:
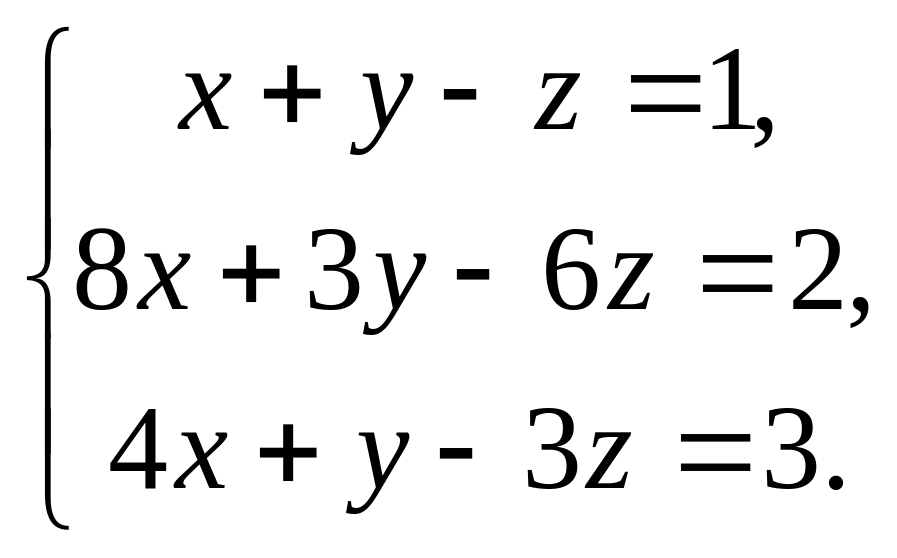
Розв’яжіть систему рівнянь:
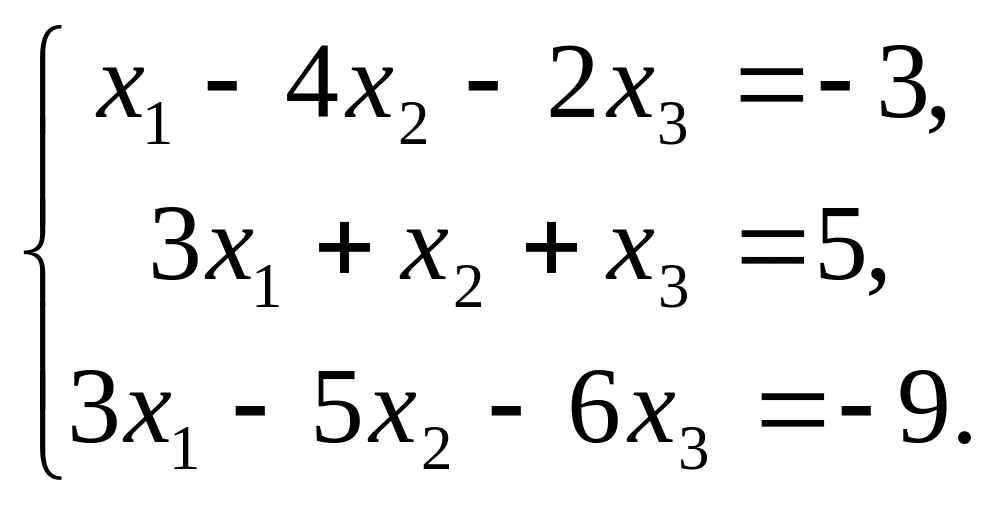
Розв’яжіть систему рівнянь:
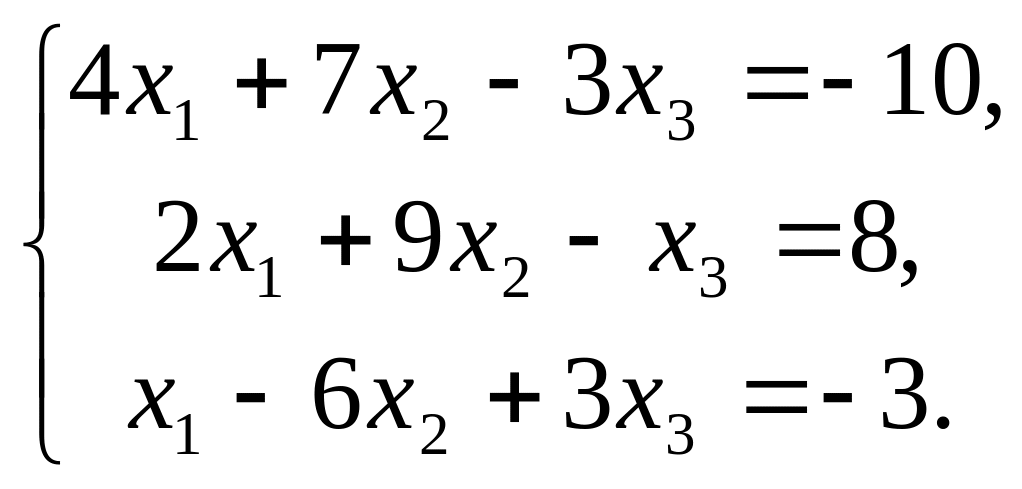
Розв’яжіть систему рівнянь:
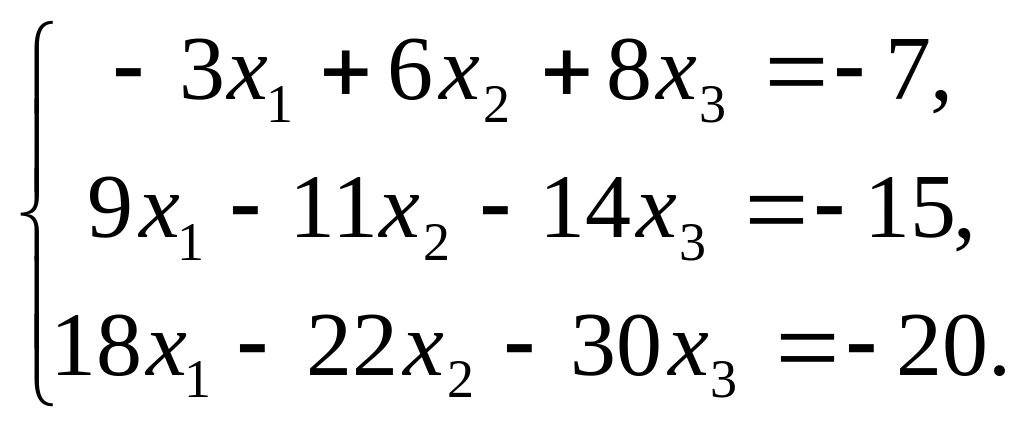
Розв’яжіть систему рівнянь:
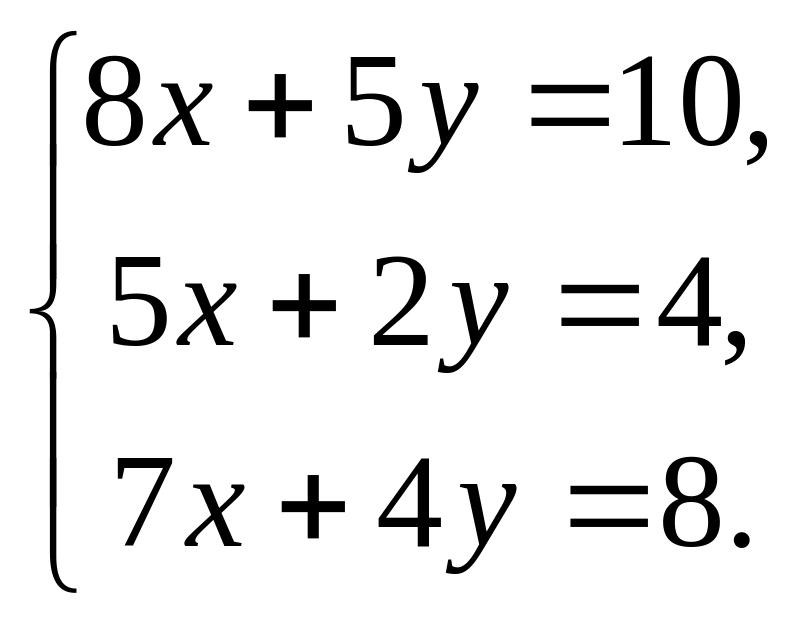
Розв’яжіть систему рівнянь:
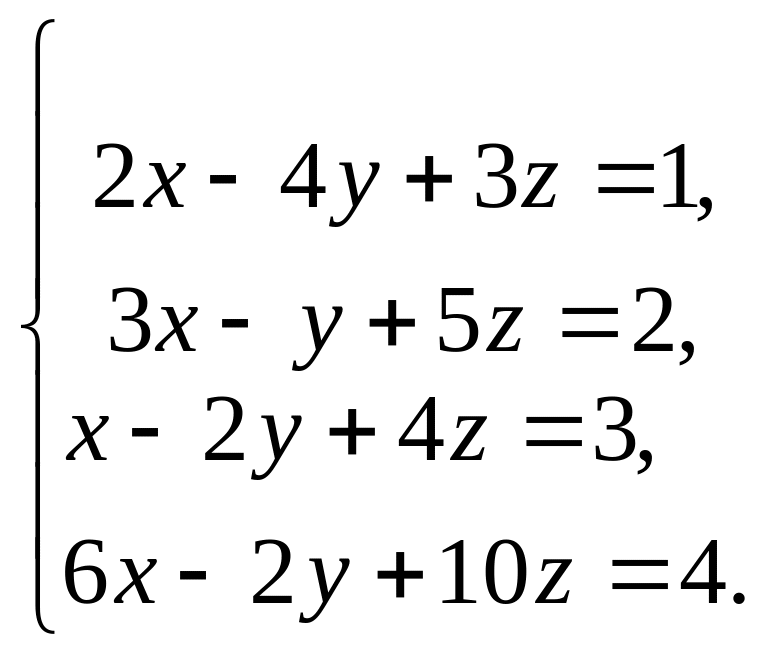
Розв’яжіть систему рівнянь:
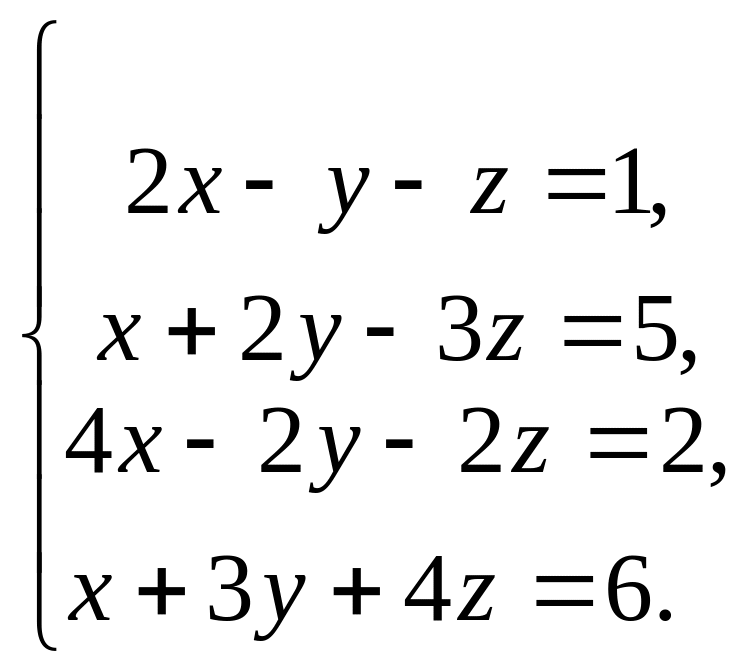
Додаток 1
Міністерство освіти і науки, молоді та спорту України
Вінницький національний технічний університет
Інститут електроенергетики та електромеханіки
Кафедра КЕЕМІГ
РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА з дисципліни "Обчислювальна техніка та алгоритмічні мови"
Варіант №1
Виконав: ст. гр. 1Е-12б
Студентов С.С.
Перевірив: доц., к.т.н.
Камінький А.В.
2012
Додаток 2
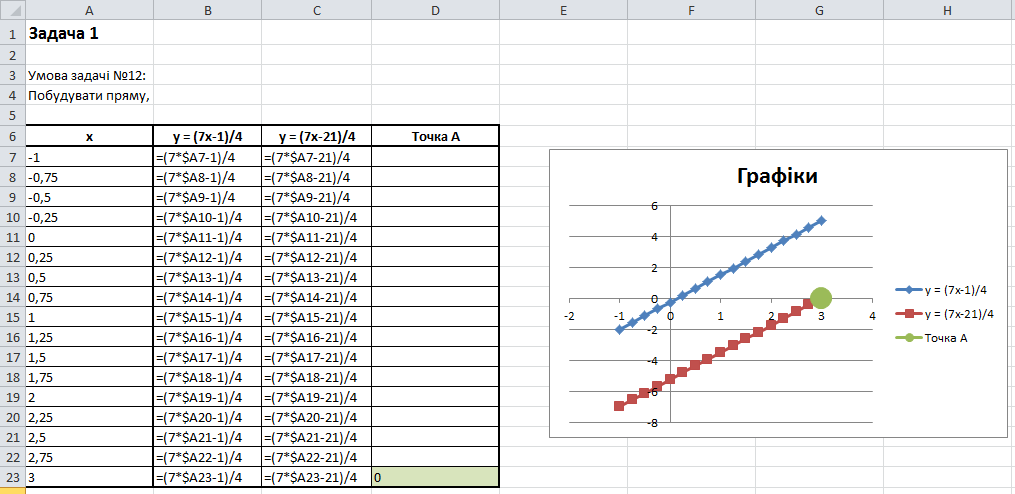
Задача 1. (№12 Розділ 1)
Розв’язок
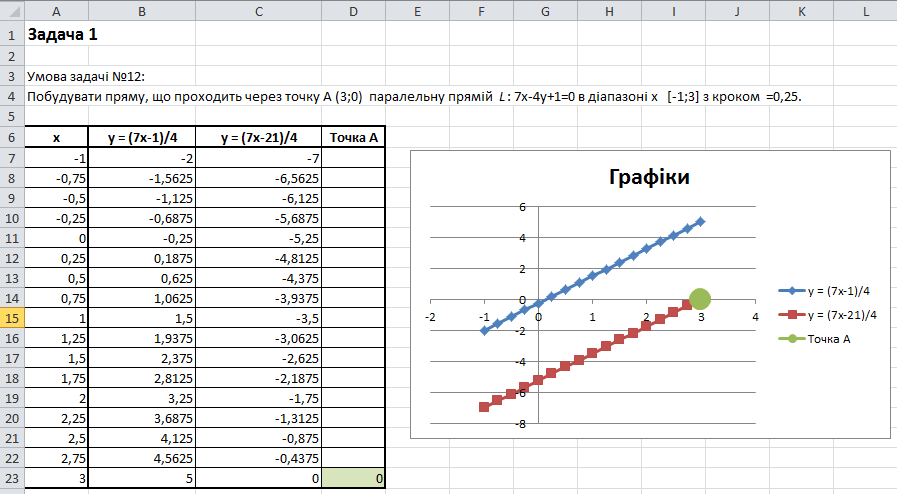
Формули