3. Справочный материал

1. ВИДЫ ПОНЯТИЙ

2. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ ПО ОБЪЕМУ

ПРАВИЛА ОПРЕДЕЛЕНИЯ

1. Соразмерность.

Определение должно быть соразмерным: объем определяемого должен быть равен объему определяющего.

Ошибки:

1. слишком широкое: объем определяющего больше объема определяемого;

2. слишком узкое: объем определяемого больше объема определяющего.

1. Запрет отрицания.

Определение не должно быть только отрицательным. Если без отрицания в определении обойтись невозможно (например, в случае отрицательного понятия), то наряду с отрицанием в определении должна быть утверждающая часть.

3. Запрет круга.

Нельзя определять понятие само через себя.

4. Запрет неясности.

Определение должно быть четким и ясным, не должно содержать неясных понятий.

4. ПРАВИЛА ДЕЛЕНИЯ

   1. Соразмерность.

Объем делимого понятия должен исчерпываться объемами понятий – членов деления.

Ошибки:

1. деление с недостающими членами;

2. деление с лишними членами.

1. Деление должно производиться по одному основанию.

2. Деление должно быть последовательным и непрерывным: при делении объема понятия от родового понятия следует переходить к ближайшему виду, а лишь затем к подвиду.

Ошибка: скачок в делении.

4. Члены деления должны исключать друг друга: члены деления должны быть несовместимыми понятиями.

4. ОБОБЩЕННАЯ КЛАССИФИКАЦИЯ СУЖДЕНИЙ (по количеству и качеству). РАСПРЕДЕЛЕННОСТЬ ТЕРМИНОВ В СУЖДЕНИИ

A – общеутвердительное E – общеотрицательное

В

S⁺⁺

се S есть P. Ни одно S не есть P.

P^-

S⁺

P⁺

I – частноутвердительное O – частноотрицательное

Н

S^-

екоторые S есть P. Некоторые S не есть P.

S^-

P^-

S^-

P⁺

Распределенным является термин, представленный в суждении в полном объеме.

4. ЛОГИЧЕСКИЕ ОПЕРАЦИИ С СУЖДЕНИЯМИ

   1. Обращение – это преобразование суждения путем перестановки его субъекта и предиката. При этом качество суждения не меняется, а количество может измениться.

Формулы обращения суждений:

(A) Все S есть P (E) Ни одно S не есть P

( I ) Некоторые P есть S (E) Ни одно P не есть S

( I ) Некоторые S есть P (O) Некоторые S не есть P

( I ) Некоторые P есть S НЕ ОБРАЩАЕТСЯ

2. Превращение – это преобразование суждения путем изменения его качества. При этом количество суждения не меняется, субъект и предикат остаются на своих местах, а понятие предиката меняется на противоположное.

Формулы превращения суждений:

(A) Все S есть P (E) Ни одно S не есть P

( E) Ни одно S не есть не-P (A) Все S есть не-P

( I ) Некоторые S есть P (O) Некоторые S не есть P

( O ) Некоторые S не есть не-P ( I ) Некоторые S есть не-P

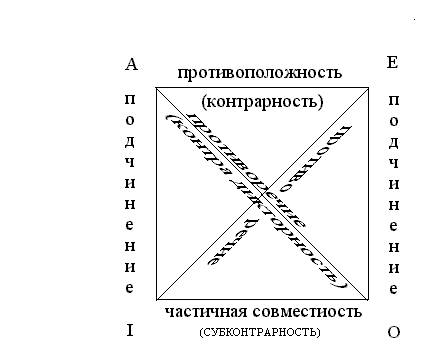4. Л ОГИЧЕСКИЙ КВАДРАТ

Закономерности отношений

1. А – I, Е – О – подчинение

   1. из истинности подчиняющего суждения следует истинность подчиненного, но не наоборот;

   2. из ложности подчиненного суждения следует ложность подчиняющего, но не наоборот.

Схемы вывода: A_И  I_И, E_И  O_И, I_ЛА_Л, O_ЛE_Л

2. I – О – частичная совместимость

Суждения могут быть одновременно истинными, но не могут быть одновременно ложными.

Схемы вывода: I_Л  O_И, O_Л I_И

3. А – Е – противоположность

Суждения не могут быть одновременно истинными, но могут быть одновременно ложными.

Схемы вывода: A_ИE_Л, E_И ®А_Л

4. А – О, Е – I – противоречие

Суждения не могут быть одновременно ни истинными, ни ложными.

Схемы вывода: A_И ®O_Л, A_Л® O_И, E_И® I_Л , E_Л® I_И, O_Л® A_И, O_И® A_Л,

I_Л ® E_И, I_И ® E_Л

4. КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ

   1. Фигуры силлогизма

1-я фигура 2-я фигура 3-я фигура 4-я фигура

2. Таблица правильных модусов

1-я фигура	AAA, EAE, AII, EIO
2-я фигура	EAE, AEE, EIO, AOO
3-я фигура	AAI, IAI, AII, OAO, EAO, EIO
4-я фигура	AAI, AEE, EAO, EIO, IAI

3. Правила силлогизма

1. Правила терминов

   • В силлогизме должно быть только три термина.

Ошибка: учетверение терминов.

• Средний термин должен быть распределен хотя бы в одной из посылок.

• Термин распределен в заключении тогда и только тогда, когда он распределен в посылке.

Правила посылок

• Из двух отрицательных посылок нельзя сделать заключение.

• Из двух частных посылок нельзя сделать заключение.

• Если одна из посылок отрицательная, то и заключение отрицательное

• Если одна из посылок частная, то и заключение частное.

9. ЛОГИЧЕСКИЕ ЗАКОНЫ

   1. Закон тождества: всякая мысль тождественна самой себе.

   2. Закон противоречия: два противоположных суждения об одном и том же предмете, взятом в одно и тоже время и в одном и том же отношении, не могут быть одновременно истинными, по крайней мере одно из них необходимо ложно.

   3. Закон исключенного третьего: два противоречащих суждения не могут быть одновременно ложными: одно из них – необходимо истинно, другое – необходимо ложно, третьего не дано.

   4. Закон достаточного основания: всякая истинная мысль имеет достаточное основание.

14