Введение

Предмет «Логика» является дисциплиной по выбору учебного заведения и изучается в соответствии с учебным планом в цикле общих гуманитарных и социально-экономических дисциплин.

Цель изучения курса – формирование логической культуры студентов.

Задачи курса:

• теоретический анализ существующих форм мышления (понятие, суждение, умозаключение) и овладение соответствующими практическими умениями;

• изучение законов правильного мышления и применение их на практике;

• овладение способами и правилами доказательства и опровержения;

• овладение приёмами практической логики.

В процессе изучения курса предусмотрены как лекционные занятия, на которых студенты усваивают теоретический материал и учатся применять его на практике, так и практические, цель которых – отработка логических умений, необходимых в будущей профессиональной деятельности, а также развитие логического мышления будущих специалистов. В соответствии с ГОС ВПО учебным планом предусматривается время на самостоятельное изучение дисциплины «Логика». В процессе самостоятельной работы студенты должны усвоить теоретические понятия, приобрести логические умения и навыки.

В результате изучения курса логики студенты должны

иметь представление:

• о роли логики в познании, науке и практике;

знать:

• формы мышления (понятие, суждение, умозаключение), их характеристики, структуру, виды, отношения между ними, правила выполнения логических операций с ними;

• основные формально-логические законы, условия их применения;

• логические основы аргументации;

уметь:

• определять виды понятий, суждений, умозаключений, виды отношений между ними, использовать круги Эйлера для иллюстрации;

• выполнять логические операции с понятиями, суждениями;

• анализировать структуру суждений, умозаключений;

• применять основные формально-логические законы при решении задач;

• делать умозаключения и анализировать их правильность;

• строить гипотезы, их доказательство и опровержение.

Следует отметить, что в настоящее время издано большое количество различных книг по такому учебному предмету как «Логика». Это учебники, учебные пособия, задачники, справочники, научно-популярные книги и даже «шпаргалки». При этом большинство из указанных изданий содержит лишь теоретический материал, иллюстрируемый рядом примеров. Задачники же, предлагая упражнения различного уровня сложности, никаким образом не обеспечивают необходимое руководство самостоятельной работой студентов.

В связи с вышесказанным возникает необходимость в дидактическом обеспечении самостоятельной работы студентов по логике, которым и является предлагаемое пособие, состоящее из двух частей. В первой части представлен краткий обзор теоретического материала по таким темам как «Понятие», «Суждение» и «Умозаключение». Во второй части представлены задания для самостоятельной работы студентов, которые предназначены для использования как в процессе аудиторных занятий, так и во внеаудиторной самостоятельной работе студентов. Результатом выполнения указанных заданий будет формирование основ логической грамотности и культуры будущих специалистов.

Вторая часть пособия представляет собой тетрадь с печатной основой, в которой приведены задания по основным темам и понятиям курса логики. Каждый вид задания снабжен примером его выполнения, что поможет студентам грамотно оформить результаты своей работы. Для выполнения каждого задания в тетради предусмотрена печатная основа, которая позволяет оптимизировать работу студентов, избавляя от необходимости переписывать условие, данные и пр. В то же время достаточно подробное описание хода рассуждений позволяет преподавателю в процессе проверки адекватно оценить работу студента, выявить пробелы в знаниях, скорректировать процесс формирования логических умений.

В конце пособия приведен необходимый справочный материал в виде схем, формул и таблиц, который будет полезен студентам как в процессе изучения курса логики, так и при дальнейшем обучении, а также в процессе самообразования.

ОСНОВНЫЕ ФОРМЫ МЫШЛЕНИЯ

ПОНЯТИЕ

Понятие как форма мышления

Понятие – форма мышления, в которой отражаются существенные (общие) признаки одного класса однородных предметов; выражается существительным, прилагательным или их сочетанием.

Возникновение понятия – не простой зеркальный акт отражения предметов действительности, а сложнейший процесс. Он предполагает активность субъекта, включает в себя множество логических приёмов. Важнейшими из них выступают анализ и синтез, сравнение, абстрагирование обобщение. Все эти логические приёмы тесно связаны между собой, образуя единый процесс. Его конечным итогом оказывается мысль, имеющая безгранично разнообразное содержание, но принимающая неизменно одну и ту же форму – понятия.

Знание процесса образования понятия даёт возможность раскрыть его действительную природу. Понятие – это форма мышления, посредством которой отражаются общие и существенные признаки предметов, взятые в их единстве. Под предметом здесь и далее будем подразумевать не только конкретные вещи, явления, процессы, но и их свойства, а также связи и отношения; предметы материальные и духовные, действительные и мнимые, уже существующие и возможные в будущем – словом, всё то, на что может быть направлена человеческая мысль, любой объект мысли. В этом состоит универсальность понятия как формы мышления, его способность отразить всё качественное многообразие и единство мира.

Понятие характеризуется относительной самостоятельностью своего существования. Предмет может исчезнуть, а понятие сохраняется, передаваясь от поколения к поколению. С изменением действительности возникают новые понятия.

Понятия выполняют две основные функции – познавательную и коммуникативную. Познавательная функция осуществляется на основе такой операции как применение понятия (или подведение предмета под понятие). Коммуникативная функция тесно связана с познавательной. Закрепляя свои знания в форме понятий, люди затем обмениваются ими в процессе совместной деятельности, а также передают их последующим поколениям. Тем самым осуществляется социальное наследование знаний, обеспечивается духовная преемственность поколений.

В понятии различаются содержание и объём. Содержание – это мыслимые в понятии общие и существенные признаки предметов. Объём понятия – это охватываемые им предметы мысли.

Виды понятий

Объективные различия между предметами мысли отражаются в различиях между понятиями, прежде всего по их содержанию. В соответствии с этим можно выделить следующие наиболее значимые группы.

1. Конкретные и абстрактные понятия.

Конкретные – понятия, в которых находят своё отражение сами предметы и явления, обладающие относительной самостоятельностью существования (например, «налог», «велосипед», «музыка»).

Абстрактные – это понятия, в которых мыслятся свойства предметов или отношения между предметами, не существующие самостоятельно без этих предметов (например, «белизна», «профессионализм», «бескорыстие»).

Необходимо учитывать известную относительность разграничения конкретных и абстрактных понятий. Так, если абстрактное понятие, отражающее свойство, употребляется применительно к самим предметам, обладающим этим свойством, то оно обретает множественное число (например, «сладость» и «восточные сладости»).

2. Положительные и отрицательные понятия.

Положительные – это те понятия, в которых отражается наличие у предметов мысли каких-либо качеств, свойств и т.д. (например, «живой», «металл», «порядок»).

Отрицательные – это понятия, которые характеризуются отсутствием у предметов мысли каких-либо качеств, свойств и т. д. (например, «неживой», «неметалл», «беспорядок»). Важно учитывать, что характеристика понятия в качестве положительного или отрицательного имеет сугубо логическое значение и не имеет ничего общего с соответствующей фактической оценкой самих предметов мысли, отражаемых ею. Например, «невиновность» – отрицательное понятие, хотя само явление положительное. «Виновность», наоборот, положительное понятие, а как явление – отрицательное.

3. Соотносительные и безотносительные понятия.

В соотносительных понятиях один предмет мысли предполагает существование другого и без него невозможен, например, «родители» и «дети».

В безотносительных понятиях мыслится предмет, существующий до известной степени самостоятельно, например, «природа», «животное», «человек».

4. Собирательные и несобирательные понятия.

Понятие называется собирательным, если им охватывается совокупность предметов, мыслимая как единое целое. Одна из особенностей собирательных понятий состоит в том, что слово, обозначающее данное понятие не может быть отнесено к каждому объекту, входящему в класс. Например, «лес» – собирательное понятие, так как им охватывается совокупность растений, мыслимая как единое целое. Кроме того, понятие лес нельзя отнести к каждому предмету данного класса: отдельное дерево, растущее в лесу – это ещё не лес.

Несобирательные понятия относятся не только к группе предметов в целом, но и к каждому отдельному предмету данной группы. Например, «учитель» – это и вся совокупность учителей в целом, и учитель математики, учитель физики, и учитель химии, и пр., и данный конкретный учитель в отдельности. Следует отметить, что одно и то же понятие может употребляться как в собирательном, так и в разделительном смысле.

Различия между предметами мысли находят своё отражение также в различиях между понятиями по их объёму. Но если виды понятий по их содержанию характеризуют качественные различия предметов, то виды понятий по их объёму – количественные различия. В соответствии с этим выделяются следующие виды понятий.

1. Пустые понятия (с нулевым объёмом) – понятия, которыми обозначены не существующие реально объекты. Например, «русалка», «вечный двигатель», «абсолютно чёрное тело».

2. Непустые понятия имеют объём, в который входит, по крайней мере, один реальный предмет: «столица России», «космический корабль», «человек».

3. Непустые понятия, имеющие единичный объём (объём понятия составляет лишь один предмет) называют единичными. Например, «Россия», «первый космонавт в мире», «человечество».

4. Если в объёме понятия заключается группа предметов (два и более) и понятие употреблено в разделительном смысле, то такое понятие называется общим. Например, «космонавт», «машина», «композитор».

5. Общие понятия могут быть регистрирующими и нерегистрирующими. Регистрирующими называются понятия, в которых множество мыслимых в нём элементов поддаётся учёту, регистрируется (по крайней мере, в принципе). Например, «участник обороны Заполярья», «планета Солнечной системы». Регистрирующие понятия имеют конечный объём. Общие понятия, относящиеся к неопределённому числу элементов, называются нерегистрирующими. Например, «студент», «животное», «ракета».

Определить, к какому виду относится то или иное понятие, – значит дать его логическую характеристику, которая помогает уточнить его содержание и объём, вырабатывает навыки более точного употребления понятий в процессе рассуждения.

Отношения между понятиями

Отношения между самими предметами находят своё отражение в отношениях между понятиями. Всё многообразие этих отношений можно классифицировать также на основе важнейших логических характеристик понятия: его содержания и объёма.

По содержанию между понятиями могут быть два основных вида отношений – сравнимость и несравнимость.

1. Сравнимые – это понятия, имеющие в своём содержании общие существенные признаки (некоторые признаки, позволяющие сравнивать понятия друг с другом). Например, «опера» и «балет».

2. Несравнимые – понятия, не имеющие сколько-нибудь существенных в том или ином отношении общих признаков. Например, «квадрат» и «музыка».

В логических отношениях могут находиться только сравнимые понятия.

По объёму сравнимые понятия могут быть совместимыми и несовместимыми. Совместимыми являются понятия, имеющие в объёмах хотя бы один общий объект. Несовместимые понятия не имеют в объёмах ни одного общего элемента. Различают по три типа совместимых и несовместимых понятий. Изображать отношения между понятиями по объёму принято в круговых схемах Эйлера (кругом обозначается объём данного понятия, за пределами круга нет ни одного объекта из объёма данного понятия).

1. Рассмотрим отношения между совместимыми понятиями.

   1. Равнозначность – объёмы понятий полностью совпадают. Например, «Москва» и «столица России».

А, В

2. П одчинение – объём одного понятия полностью содержится в объёме другого понятия. Например, «человек» и «студент».

А

В

3. Перекрещивание – объёмы понятий совпадают лишь частично (в объёмах понятий есть общая часть и различные). Например, «студент», «музыкант».

А В

2. Рассмотрим несовместимые понятия.

   1. С оподчинение – понятия не имеют в объёмах ничего общего, но по отдельности подчинены одному и тому же понятию. Например, «спортивная игра», «футбол», «баскетбол».

А

В С

2. Противоречие – в этом отношении находятся положительное и соответствующее отрицательное понятия. Например, «умный человек» и «неумный человек».

А

не – А

3. Противоположность – в этом отношении находятся понятия с противоположными признаками. Например, «храбрость» и «трусость».

А В

Логические операции с понятиями

1. Определение – логическая операция, раскрывающая содержание понятия. Например: «Квадрат – это прямоугольник, у которого все стороны равны».

Понятие, содержание которого раскрывается в определении – определяемое; понятие, посредством которого раскрывается содержание понятия – определяющее.

Правила определения.

1. Соразмерность. Определение должно быть соразмерным, то есть объём определяющего должен быть равен объёму определяемого.

При нарушении этого правила возникают две ошибки.

1. Слишком широкое определение (объём определяющего больше, чем объём определяемого). Например: «Студент – это человек, который учится». В данном случае невозможно отличить студента от школьника или специалиста, повышающего свою квалификацию.

2. Слишком узкое определение (объём определяемого больше, чем объём определяющего). Например: «Студент – это человек, который учится в педагогическом университете». В соответствии с данным определением человек, который учится в техническом университете, студентом не является.

1. Запрет круга. Нельзя определять понятие само через себя. Например: «Вращение – это движение тела вокруг своей оси». В данном определение нарушено правило запрета круга, так как «ось – это прямая, вокруг которой происходит вращение».

2. Запрет отрицания. По возможности определение не должно быть отрицательным. При определении отрицательных понятий наряду с отрицанием определение должно содержать утверждение. Например, неправильным будет такое определение: «Атеизм – это отрицание Бога». Более правильно будет следующее определение: «Атеизм – это отрицание Бога и утверждение бытия на Земле».

3. Запрет неясности. Определение должно быть ясным и чётким. Это означает, что содержание и объём понятий, содержащихся в определяющем, должны быть ясными, определение не должно содержать недвусмысленности.

2. Деление – это разбиение объёма понятия на части по какому-либо признаку. Понятие, объём которого разбивается, называется делимым; признак, по которому осуществляется разбиение – основание деления; а части, на которые разбивается объём исходного понятия – члены деления. Например, студенты делятся на успевающих и неуспевающих.

Правила деления.

1. Объём делимого понятия должен полностью исчерпываться объёмами членов деления.

При нарушении этого правила возможны две ошибки.

1. Деление с недостающими членами. Так, неверным будет деление понятия «власть» на законодательную и исполнительную ветвь. В этом случае недостающий член деления – судебная ветвь власти.

2. Деление с лишними членами. Выделение из понятия «власть» наряду с законодательной, исполнительной и судебной ветвями власти средств массовой информации как четвёртой ветви является неправильным. Объём понятия «власть» полностью исчерпывается первыми тремя, а «средства массовой информации» – лишний член деления.

1. Деление должно производиться по одному основанию. Так, неверным будет следующее деление объёма понятия «студент»: успевающие, неуспевающие и ленивые.

2. Члены деления должны исключать друг друга. Члены деления должны быть соподчинёнными понятиями, то есть не иметь общих элементов в объёмах. Так, неверным будет деление понятия «студент» на успевающих, неуспевающих и отличников. Член деления «отличники» уже входит в объём понятия «успевающие».

3. Деление должно быть последовательным и непрерывным. При делении следует от родового понятия переходить к видовым, а только затем к подвидовым, то есть нельзя при делении делать скачков. Так, нельзя удобрения разделить на органические, азотные, калийные и фосфорные. Сначала удобрения делятся на органические и минеральные, и только затем минеральные можно разделить на азотные, калийные и фосфорные.

2. Обобщение – это логическая операция перехода от понятия с меньшим объёмом и большим содержанием к понятию с большим объёмом и меньшим содержанием. Ограничение – это логическая операция перехода от понятия с большим объёмом и меньшим содержанием к понятию с меньшим объёмом и большим содержанием. Так, обобщением понятия «студент» может служить понятие «человек», а ограничением – понятие «студент первого курса».

С У Ж Д Е Н И Е

Суждение как форма мышления

Суждение – это форма мышления, в которой что-либо утверждается или отрицается о данном понятии, его свойствах или отношениях с другими понятиями. В речи суждение выражается повествовательным предложением. Каждое суждение имеет значение истинности и может быть истинным или ложным. Например, «Все студенты сдают экзамены», «Некоторые школьники не являются отличниками», «Озёра бывают солёными», «Число 10 меньше 3».

В суждении есть субъект – то понятие, о котором что-либо утверждается или отрицается, предикат – то, что утверждается или отрицается о понятии, логическая связка – «есть» или «не есть» и квантор – «все», «некоторые», «ни один». Общая формула суждения: «S есть (не есть) P».

Виды суждений

Характеристиками суждения являются качество и количество. Качество суждения определяется характером логической связки: положительное («есть») и отрицательное («не есть»). Количество зависит от того, обо всех предметах класса идёт речь в суждении или только об их части. По количеству суждения могут быть общими (в суждении говорится обо всех объектах, входящих в понятие) и частными (в суждении представлена лишь часть объектов, входящих в понятие). Например, «Некоторые птицы не летают», «Граждане России имеют право на образование», «Грибы бывают ядовитыми».

В логике применяется объединённая классификация суждений по количеству и качеству. Рассмотрим её, изобразим при этом суждения с помощью круговых схем Эйлера (для этого необходимо определить отношения между субъектом и предикатом суждения). По количеству и качеству можно выделить четыре вида суждений.

1. О бщеутвердительное суждение A. Например, «Все тигры (S) – млекопитающие (P)». В общем виде: «Все S есть P».

P

S

2. О бщеотрицательное суждение E. Например, «Крокодилы (S) не летают (P)» (в явной логической форме: «Ни один крокодил (S) не летает (P)»). В общем виде: «Ни одно S не есть P».

S P

3. Частноотрицательное суждение O. Например, «Некоторые студенты (S) не являются отличниками (P)». В общем виде: «Некоторые S не есть P».

4. Частноутвердительное суждение I. Например, «Некоторые студенты (S) работают (P)». В общем виде: «Некоторые S есть P».

S P

В суждениях термины S и P могут быть распределены и не распределены. Термин считается распределённым, если он представлен в суждении в полном объёме (объём понятия целиком входит в объём другого понятия или целиком исключается из него). Термин считается нераспределённым, если он представлен в суждении частично (объём понятия включается в объём другого понятия частично или частично исключается из него).

Так, субъект суждения S распределён в общеутвердительном и общеотрицательном суждении (S⁺) и не распределён в частноутвердительном и частноотрицательном суждении (S^-). Предикат суждения P распределён в общеотрицательном и частноотрицательном суждении (P⁺) и не распределён в общеутвердительном и частноутвердительном суждении (P^-).

Отношения между суждениями

Суждения, как и понятия, могут быть сравнимыми (имеют общий субъект и предикат) и несравнимыми (субъект и/или предикат различны). Сравнимые суждения по значениям истинности бывают совместимыми (выражают одну и ту же мысль полностью или в некоторой части) и несовместимыми (из истинности одного из них с необходимостью следует ложность другого).

Отношения совместимости: эквивалентность, подчинение и частичная совместимость. Отношения несовместимости: противоположность и противоречие.

Совместимые эквивалентные суждения выражают одну и ту же мысль в различной форме. Например, «Все защитники в суде имеют юридическое образование» и «Все адвокаты – юристы».

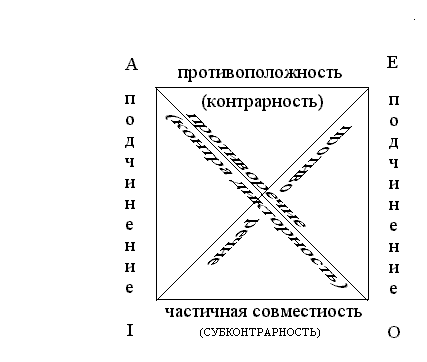Отношения между суждениями по значениям истинности принято схематически изображать в виде так называемого «логического квадрата».

Рассмотрим закономерности, выражающие отношения между суждениями по значениям истинности.

1. Суждения A – I и E – O находятся в отношении подчинения. Суждения A и E – подчиняющие, а I и O – подчинённые.

   1. Если подчиняющее суждение истинно, то и подчинённое истинно.

   2. Если подчинённое суждение ложно, то и подчиняющее ложно.

2. Суждения I – O находятся в отношении частичной совместимости. Оба они одновременно могут быть истинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое обязательно истинно.

3. Суждения A – E находятся в отношении противоположности. Они могут быть одновременно ложными, но не могут быть одновременно истинными. Если одно из них истинно, то другое обязательно ложно.

4. Суждения A – O и E – I находятся в отношении противоречия. Они никогда не имеют одинаковых значений истинности. Если одно из суждений пары истинно, то другое обязательно ложно; если одно из суждений пары ложно, то другое обязательно истинно.

Закономерности, выражающие отношения между суждениями по значениям истинности, имеют большое познавательное значение, так как они помогают правильно делать непосредственные умозаключения (умозаключение из одной посылки).

Логические операции с суждениями

Превращение – это преобразование суждения путём изменения его качества. При этом количество суждения и его субъект не меняются, а понятие предиката меняется на противоположное. Например:

1. Подлежащее – главный член предложения.

(E) Подлежащее не является второстепенным членом предложения.

Обращение – это преобразование суждения. При котором субъект исходного суждения становится предикатом, а предикат исходного суждения становится субъектом. При этом качество суждения не меняется, а количество может измениться. Например:

(A) Все композиторы – музыканты.

9. Некоторые музыканты – композиторы.

У М О З А К Л Ю Ч Е Н И Е

Умозаключение как форма мышления

Умозаключение – это форма мышления, посредством которой из одного или нескольких истинных суждений с помощью определённых правил вывода получается новое истинное суждение. Умозаключения бывают дедуктивными, индуктивными и по аналогии.

В дедуктивном умозаключении мысль движется от общего к частному. При соблюдении правил вывода заключение является истинным суждением. В индуктивном умозаключении мысль движется от частного к общему. Вывод является вероятным. При умозаключении по аналогии мысль движется от частного к частному. Вывод при этом носит вероятный характер.

Категорический силлогизм

Категорический силлогизм (простой категорический силлогизм) – это вид дедуктивного умозаключения, в котором из двух истинных простых суждений при соблюдении правил вывода получается новое истинное суждение. Например:

Жидкости (M) упруги (P). – большая посылка

Вода (S) – жидкость (M). – меньшая посылка

Вода (S) упруга (P). – заключение

Понятия «жидкость», «вода» и «упруга» называют терминами силлогизма. S («вода») – субъект заключения, содержится в меньшей посылке и называется меньшим термином. P («упруга») – предикат заключения, содержится в большей посылке и называется меньшим термином. М («жидкость») – содержится в обеих посылках, отсутствует в заключении, служит для связи посылок и называется средним термином.

С иллогизм можно изобразить в круговых схемах Эйлера. Для этого необходимо изобразить посылки, а затем осуществить их совмещение. Так, схемой приведённого выше силлогизма будет следующая:

P

M S

Фигурами силлогизма называются формы силлогизма в зависимости от положения среднего термина. Всего может быть четыре фигуры силлог

1-я фигура 2-я фигура 3-я фигура 4-я фигура

Модусами фигур силлогизма называют разновидности силлогизма, отличающиеся друг от друга качественной и количественной характеристикой входящих в него посылок и заключения. Всего различных модусов существует 256, из них только 19 правильных, по которым можно получить достоверное заключение. По каждой фигуре правильные модусы представлены в таблице (см. справочный материал в конце пособия).

В наших рассуждениях мы часто пользуемся категорическим силлогизмом. Для того чтобы получать правильные выводы, необходимо соблюдать общие правила силлогизма (см. справочный материал в конце пособия). Также практически часто необходимо бывает оценить достоверность полученного в рассуждениях умозаключения. Категорический силлогизм можно проверить разными способами.

Способы проверки категорического силлогизма

1. Проверка по фигуре и модусу. Для того чтобы воспользоваться этим способом проверки, необходимо построить фигуру полученного силлогизма, определить его модус, а затем обратиться к таблице правильных модусов. Если по данной фигуре полученный модус правильный, значит. Выводу можно доверять. Если среди правильных модусов по построенной фигуре полученный модус не числится, значит, выводу доверять нельзя.

2. Проверка с помощью круговых схем Эйлера. Проверяя силлогизм указанным способом, следует построить в круговых схемах его посылки, а затем их совместить. Если при совмещении получается единственный вариант, соответствующий полученному выводу, значит, заключение получено верное. Если же при совмещении посылок возможны различные варианты круговых схем, значит, полученному выводу доверять нельзя.

3. Проверка по общим правилам силлогизма. В данном случае полученный силлогизм проверяется на соответствие общим правилам. Если хотя бы одно из правил не выполняется, то вывод некорректен. Если же все правила выполняются, то силлогизм построен верно, вывод – верен.

4. Приведением контрпримера. Вместо одного из терминов силлогизма (S или P) подставляется новое понятие так, чтобы посылка оставалась истинной. Если вывод получается абсурдный, то это доказывает, что силлогизм построен неверно, и выводу доверять нельзя.