2.4 Решение задач.

Рассмотрим применение теоремы Пифагора в школьном курсе геометрии. Воспользуемся, прежде всего, возможностями, которые даёт теорема Пифагора для вычисления длин отрезков некоторых известных нам фигур:

Задача 1:

Дано: Треугольник ВСЕ - прямоугольный с гипотенузой DE (см. рис. 12)

Решение:

по теореме Пифагора:

DЕ² = DC² + СЕ², DС² = DЕ² - СЕ², DС² =52 - 32, ВС² = 25-9, В DС² = 16,

Рис.12

Ответ: DC = 4

Получили прямоугольный треугольник со сторонами 3, 4, и 5 ед. Это единственный прямоугольный треугольник, стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, т.к. он был известен ещё древним египтянам. Они использовали этот треугольник в «правиле верёвки» для построения прямых углов при закладке зданий, храмов и алтарей.

Задача 2:

Дано:

Из одного порта вышли два корабля: один – на восток, другой – на север.

Расстояние от главного порта до порта на востоке – 300 миль, а до порта на севере – 400 миль. Каково расстояние между двумя портами?

Решение 1:

Угол между курсами кораблей будет составлять 90 , отрезок, соединяющий порты назначения является гипотенузой (х) треугольника, вершинами которого являются порты назначения и главный порт. Следовательно, из условия задачи нам известны длины катетов прямоугольного треугольника.

По теореме Пифагора:

х = 300 + 400 = 250000,

х = ,

х = 500.

Ответ: 500 миль от восточного порта до северного.

Решение 2:

Используя понятие египетского треугольника ( стороны которого равны 3,4 и 5) мы можем решить эту задачу, не проводя вычислений, т.е. гипотенуза прямоугольного треугольника равна 500 миль.

Ответ: 500 миль от восточного порта до северного.

Задача 3:

Какую наибольшую высоту должна иметь телевизионная вышка, чтобы передачу можно было осуществить в радиусе R=200 км? ( R Земли =6380 км).

Рис. 13

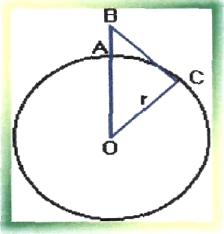Решение:

Пусть АВ= х, ВС=R=200 км, ОС= r =6380 км, ОВ = OА+АВ,

ОВ = r + х, ВС является касательной к окружности в точке С, значит угол ОСВ = 90 , следовательно треугольник ОСВ прямоугольный, где ОВ - гипотенуза.

Используя теорему Пифагора, получим:

X =√ (r²+R²) - r = - 6380 6383,13 – 6380 3,13 км

Ответ: телевизионная вышка должна иметь высоту не менее чем 3,13 км.

Задача 4:

Дано:

Угол КLМ вписан в окружность и опирается на диаметр КМ, КL=5, LМ=12, найти диаметр окружности (см. рис.14).

Решение:

Так как вписанные углы, опирающиеся на диаметр, - прямые, то угол КLМ - прямой. Значит, треугольник КLМ - прямоугольный.

Рис.14.

По теореме Пифагора для прямоугольного треугольника КLМ с гипотенузой КМ:

КМ² = КL² + LМ²= 5² + 12²=169,

К М=√169 = 13.

Рис.15

Ответ: диаметр окружности равен 13 Задача 5: (из китайской «Математики в девяти книгах» )

Дано:

«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?»(см. рис. 15).

Решение:

1. Пусть глубина водоёма равна х, согласно условиям задачи расстояние от камыша до берега равна половине ширины водоема, т.е. 5 чи. Треугольник, образованный камышом, растущим со дна и наклонённым к берегу, и поверхностью водоёма, является прямоугольным, в котором поверхность водоёма (5 чи) и растущий камыш (х чи) являются катетами, а наклонённый камыш((х+1) чи) является

гипотенузой данного треугольника.

2.Согласно теореме Пифагора,

(х+1) ² = х² +5² ,

х²+2х+1-х² = 25,

2х = 24,

x=12

3. Глубина водоёма составляет 12 чи, а длина камыша равна глубина водоёма + 1=13 чи.

Ответ: Глубина водоёма равна 12 чи, а длина камыша – 13 чи.

Задача 6:

Дано:

Рис.16

«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготъю 125 стоп. И ведати хочет, колико стоп сея лестницы пилений конец от стены отстояти имать» (см. рис.16).

Решение:

1. Обозначим основание стены – С , соединение лестницы со стеной – А, а основание лестницы – В, в результате получили треугольник АВС, в котором угол ВСА прямой. Согласно условию задачи катет АС=117(стоп), гипотенуза АВ=125(стоп).

2. Согласно теореме Пифагора АВ² = АС² + СВ² ,

СВ² = АВ² - АС² = 125²-117² = 1936,

СВ = = 44( стопы)

Ответ: основание лестницы надо расположить на 44 стопы от стены. Задача 7 : (индийского математика ХII века Бхаскары) (Рис. 17)

Дано:

Рис.17

«На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?» (см.рис.17)

Решение:

1. Обозначим основание тополя – С, соединение вершины тополя с противоположным берегом реки –А, точку надлома тополя – В, а вершину тополя – D, в результате получили треугольник АВС, в котором угол ВСА прямой. Согласно условию задачи катет АС = 4(фута), катет СВ = 3(фута).

2.Согласно теореме Пифагора АВ² = АС² +СВ²,

АВ² = СВ² +АС² = 3²+4² = 25,

АВ = √25 = 5 ( футов)

3.Высота всего тополя равна CD = CB + BD, т.к. BD = АВ = 5 футов, то СD = 3+5 = = 8 (футов).

Примечание: используя понятие египетского треугольника решение данной задачи может быть следующим: т.к. треугольник АВС прямоугольный и катеты равны 3,4 футам, то гипотенуза равна 5 футам, высота тополя соответственно равна 8 футам.

Ответ: высота тополя составляет 8 футов.