5 Расчет на продавливание

Данный расчет производится в предположении, что разрушение происходит по поверхности пирамиды, боковые поверхности которые наклонены под углом 45⁰ к вертикали.

Строим пирамиду продавливания. Чертеж приведен в приложении Б.

После построения, получили следующие размеры нижнего основания пирамиды продавлиания:

b_осн = 1700 мм;

l_осн = 2300 мм;

F = N, кН – расчетная продавливающая сила;

F = 872,834 кН.

P_гр – давление грунта на единицу площади подошвы фундамента;

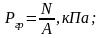
A – площадь подошвы фундамента, м²;

F=N-А_осн ·Р_гр

А_осн=l_п·b_п

l_п =l-70=2300-70=2230 мм;

b_п=b-70=1700-70=1630 мм;

А_осн=1,63·2,23=3,472 м²

F=872,834-3,472·233,378=62,546 кН;

Продавливание не происходит при выполнении следующего условия:

F ≤ α · R_bt · h₀ · U_m;

α – коэффициент, зависящий от плотности бетона, принимаем:

α = 1, для тяжелого бетона В15;

R_bt – расчетное сопротивление бетона растяжению, принимаем:

R_bt = 0,75 МПа, для тяжелого бетона В15;

С учетом коэффициента устойчивости работы бетона

R_bt = 0,75·1.1=0,825 МПа

h₀ – рабочая высота сечения фундамента на проверяемом участке;

h₀ = d_ф – a, м;

а – защитный слой бетона, принимаем:

а = 35 мм;

h₀ = 1200 мм – 35 мм = 1165 мм = 1,165 м;

U_m – среднее арифметическое между периметрами верхнего и нижнего оснований пирамиды продавливания;

U_m = 2 · (b_к + l_к + 2 · h₀), м;

b_к, l_к – стороны верхнего основания пирамиды продавливания;

U_m = 2 · (500 + 800 + 2 · 1165) = 7260 мм = 7,26 м;

α · R_bt · h₀ · U_m = 1 · 825 кПа · 1,165 м · 7,26 м = 6977,768 кН;

F = 62,546 кН < α · R_bt · h₀ · U_m = 6977,768 кН, условие выполняется;

h₀ = 1165 мм < d_ф = 1200 мм, то прочность фундамента на продавливание обеспечивается.

6 Армирование фундамента

Для определения сечения арматуры нижней ступени, вычислим изгибающий момент в каждой ступени. [3]

6.1 Изгибающий момент в сечении I – I:

М_I = 0,125 · Р_{гр ·} (l – l_к)² · b, кН · м;

­M_I = 0,125 · 233,378 · (2,3 – 0,8)² ·1,7 = 111,584 Н∙м.

Необходимая площадь сечения арматуры:

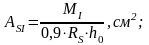
где R_S = 280МПа – расчетное сопротивление растяжению

стержневой арматуры класса А – II;

6.2 Изгибающий момент в сечении II – II:

М_II = 0,125 · Р_{гр ·} (l – l₁)² · b, кН · м;

l₁ – длина второй ступени фундамента, м;

­M_II = 0,125 · 233,378 · (2,3 – 1,3)² ·1,7 = 49,593 кН · м.

Необходимая площадь сечения арматуры:

6.3 Изгибающий момент в сечении III – III:

М_III = 0,125 · Р_{гр ·} (l – l₂)² · b, кН · м;

l₂ – длина третей ступени фундамента, м;

­M_III = 0,125 · 233,378 · (2,3 – 1,8)² · 1,7 = 12,398 кН · м.

Необходимая площадь сечения арматуры:

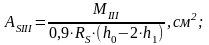
Выбор арматуры осуществляем по максимальному значению A_S;

В нашем случае максимальное значение: A_SI = 17,6 см².

Выбираем арматуру класса А–II с диаметром стержней 10 мм и их числе n = 4, площадь сечения A_S = 3,14 см². Масса 1м стержня m = 0,617 кг.[3]

Фундаменты армируют по подошве стальными сетками из стержней периодического профиля. Диаметр стрежней должен быть не менее 10 мм, а шаг – не более 200 мм и не менее 100 мм.

Определим расстояние между стержнями арматуры.

Расстояние между продольными стержнями арматуры:

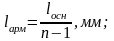
l_осн – длина основания пирамиды продавливания;

n – число стержней;

Расстояние между стержнями больше допустимого, принимаем диаметр стрежней 10 мм.

Количество стержней в продольном направлении:

Округляем в большую сторону, принимаем n_прод = 16.

Определим расстояние между стержнями в продольном направлении:

Расстояние между поперечными стержнями арматуры:

b_осн – ширина основания пирамиды продавливания;

n – число стержней;

Расстояние между стержнями больше допустимого, принимаем диаметр стрежней 10 мм.

Количество стержней в поперечном направлении:

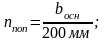
Округляем в большую сторону, принимаем n_поп = 13.

Определим расстояние между стержнями в поперечном направлении:

Окончательно принимаем арматуру класса A–II, при диаметре стержней 10 мм.

Схема армирования фундамента приведена в приложении В.