7.Лінійні р-ня n-го порядку з сталими коефіцієнтами.

Розгл.однор р-ня з сталими коефіцієнтами

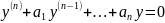(1)

Будемо шукати частк розв р-ня (1) у вигляді 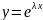(*).Підставим вираз(*) у р-ня (1).

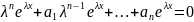
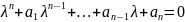(2)

Р-ня (2) називається характер. р-ням р-ня(1). Отже, р-ня(1) має частк розв.виду (*) тоді,коли 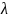є коренем характ. р-ня.

Розгл декілька випадків,щодо коренів р-ня(2).

1.Р-ня(2) має n коренів 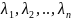,які є дійсними та попарно різними.У цьому випадку маємо множину розв р-ня(1) 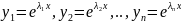.Покаж,що утвор. мн розв є фундам сист.

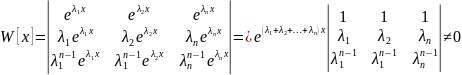
Цей детермінант наз детер.Вандермонда і він ≠0 при різних .

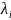У цьому разі загал розв р-ня(1) має вигляд. .

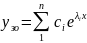2.Серед коренів характ р-ня є комплекс корені 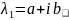.Очевидно число 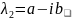теж є коренем р-ня (2).Викор (*) запиш частк розв р-ня(1). .

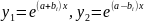Викор формулу Ейлера запиш 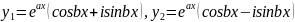.Перев чи розв є лінійн незалежн

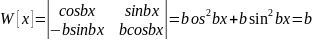.Отже,розв є лінійн незал.Тобто,кожній парі компл коренів у ФСР р-ня(1) відпов пара ф-й виду 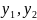,які є дійсн ф-ями.

3.Характ р-ня має кратні корені.

а)Прип,що р-ня має кратний корінь 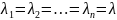Тоді 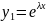його частк розв.Підсав його в р-ня(1),маємо

.

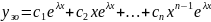б)Прип,що комплексне, тобто 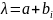. Тоді коренем характ р-ня є спряжене до к-однакових коренів.У цьому разі

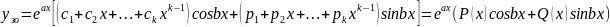
Розг неоднор р-ня L[y]=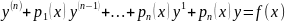 і розгул деякі рекоменд щодо його розв.

1.1)Запиш характ р-ня відпов однор р-ня та знаходь його розв.

2)запиш ФСР однор р-ня.

3)Загал розв неоднор р-ня знаходь методом Лагранжа(варіації довільної сталої).

2.1) Запиш характ р-ня відпов однор р-н.

2)Запиш загал розв однор р-ня.

3)Знаход частк розв неоднор р-ня.

4)Сума двох цих розв є загал розв неоднор р-ня.

У деяких випадках ф f(x) можна знайти методом не визнач коефіц.