5.Рівняння, що не розв’язні відносно похідної. Рівняння Лагранжа та Клеро.
це
рівняння,
що не розв’язні відносно похідної.
Перше, що треба зробити – це постар.
розв р-ня відн. похідн. припустимо, що
це вдалося зробити і при цьому одерж.
такі р-ня:
слід розв. кожне з k
р-нь окремо. при цьому об’єднання заг.
розв. цих р-нь, або їх загал. інтегр.
назив. загальн. інтегралом. р-ня (1).
Зауваження. Під особливою точкою площини розуміють точку через яку проходять хоча б 2 інтегральні криві різних рівнянь (2) дотичні до яких в цій точці різні.
Р-ня Лагранжа
при
цьому ф-ї вваж. непер. дифер. Шукаємо
розв’язок цього рівняння у параметричній
формі, тобто виразимо х та у через
параметр. Позначимо
залишається
виразити х через параметр p.
Ост. р-ть диф. по х.
.
;
Одерж.
лінійне неоднорідне рівняння.
Припустимо
Тоді
ф-я
- є також розвязок р-ня Лагранжа.
Р-ня Клеро
Якщо
має
місце
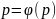то
р-ня Лагр. набир. вигл.
ост.
р-ть наз. р-ням Клеро. це частк. вип. р-ня
Лагр.
1.
ост.
р-тю визн. сім’я розв’язків р-ня, яку
називають загальним розв’язком р-ня
Клеро.
2.
Прийнято назив заг розв.
р-ня Клеро, а розв.
його особл. Розв-м.
є однор. сім’я кривих. Запиш. р-ня, які
визн. її дискр. криву.
перех. до р-ті .
,
де замість р поставлено с. особлив.
розв. р-ня Клеро визн. дискримінантну.
криву сім’ї прямих.
6.Лінійні рівняння n-го порядку. Фундаментальна системи розв. Однор. Р-ня. Детермінант Вронського. Загал. Розв.
Озн.
Розглянемо оператор
Де
-ф-я
неперервна на
y(x)
– диф.
до n-го
порядку ф-я.
Рівняння
- визн.
на (a,b)
Називають
відпов. однорідн. та неоднор. лін р-ням
n-го
порядку.
Очевидно, що опер. L[y] є лінійн. Це легко перевірити.
Заув. Якщо ф-я y1(x), y2(x),…, yk(x) є розв. р-ня (1) то їх лін. комб. теж є розв. цього р-ня.
Озн.
Множина ф-цій y1(x),
y2(x),…,
yk(x)(3)
назив. лінійно залежн. на
серед яких хоча б 1 відм. від нуля такі,
що
,у
протил. вип. ця ф-я назив. лін. незалежною.
Озн.
Множину
(3) розв’язків р-ня 1 називається її
фундаментальною системою розв’язків
якщо вона є лінійно-незалежною на
проміжку
.
– називають
детермінант Вронського с-ми ф-цій (3).
Заув.
З
лінійної залежності функцій (3) випливоє
що
Т. Якщо сист-ма розв. (3) в р-ні (1) лін. незал. на (a,b), то в кожній точці цього відр. її детерм. Врон. не дорівн. 0.
Д.
Прип. супротивне, що
(4)
Ця
с-ма є однррідна. алгебр. сист. детерм.
цієї с-ми співп. з
.
У
цьому випадку вказана система має не
нулеві розвязки оберемо один із них
.
Розглянемо ф-цію
Легко
бачити, що ф-я є розв. р-ня (1). С-ма розв.
рівняння виду (1) має розв’язок y=0.
Похідн. від ф-ї є лін. залежн., що супер. умові теореми.
Т.ч.
такої т. x0
Отже,мн
розв є лін залежн,а отже,не є фср.А це
суперечить умові,яка і довод теорему.
Н. фундам. с-ма розв. і їх є неск. багато.
Т. роз-к р-ня (1) є лінійною комб. з його фунд. с-ми розв.
Н.
Заг. розв. р-ня (1) можна зобр. у вигл.
де
-
утвор. фунд. сист розв.(3),
-довільні
сталі.
А загал розв неоднор сист – уз.н.=учн+узо,де учн=у1чн+учо.