2.Рівняння в повних диференціалах

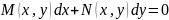(1).Будем вважати,що в прямокутникуП.a<=x<=b, c<=y<=d функції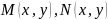 мають непер частин похідні другого порядку.

Рн-я 1 називають рівнянням у повних диференціалах якщо його ліва частина є повним диференціалом деякої функції Ф(х,у), яка має неперервні похідні по кожному аргументу до другого порядку включно.

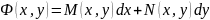=0 =>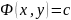 , тобто цим виразом визначається загальний інтеграл рівняння1.

Треба знайти необхідну умову, для того щоб р-ня 1 було рівнянням у повних диференціалах. Припустимо, що це так:

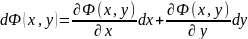
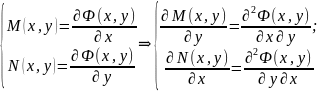
Оскільки похідні 2 порядку від функції Ф неперервні за умовою то вони рівні за теоремою з мат. аналізу, тому 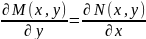- необхідна умов. існ. ф-ї 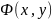., що є і достатньою умовою.

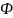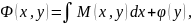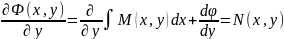
При умові викон. і побуд. потр. ф-ю : продиф. її по y. 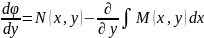не зал. від x , це р-ня з відокр. зм., знах. один з його розв. 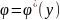і запиш. заг. інтегр. р-ня (1).

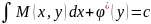
Прип. що р-ня (1) не є р-ням в повних дифер. тоді доцільно застосув. інтегральний множник

Озн. Диф. ф-я 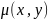назив. інтегрув. множн. р-ня (1), якщо р-ня 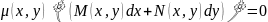(2) є р-ням у повних дифер.

,

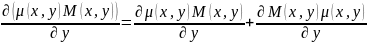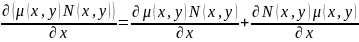
Множник 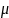необхідно підібрати так, щоб праві частини двох рівностей були рівними. Може статися, 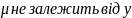тобто 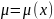Тоді запиш р-ня у вигл 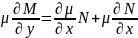, , 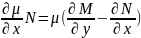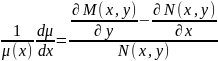.Зауваж,що прав частин не залеж від . З остан р-ня знаходь і підстав в р-ня(2).Одерж р-ня в повн диф,яке вже вміємо розв.Якщо вказана ознака не викон,слід розгул другий випадок.

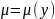тоді 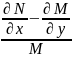– не зал від x. і 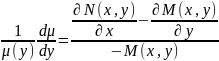.Одерж р-ня є р-ням в повн дифер,яке ми вміємо розв.

3.Лінійні рівняння першого порядку

Озн. Р-ня 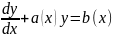, (1) де a(x), b(x) неперервні на(a,b), b(x)≠0 назив. неоднор. лін. р-нями 1-го порядку. у випадку b(x)=0 р-ня назив. однорідн. 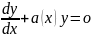(2).

1O Метод Лагранжа( варіації довільною сталою)

Розгл. одноріднетр-ня (2), яке є р-ням з відокр. змінними.

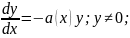
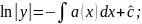
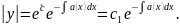с₁ є R. Шукаємо розв’язок 1 у вигляді (*) будем вваж, що c є невідомою ф-єю, задача полягаэ в тому щоб знай. знач. індек. так, щоб вир. (*)став розв. р-ня (1).

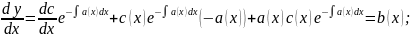
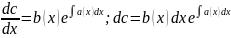
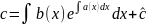Отже,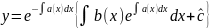 є загал розв неоднор р-ня.

20 Метод Бернуллі

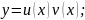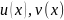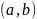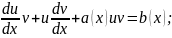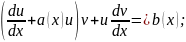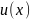
Провед. заміну змін. де невідомі дифер. ф-ї на Підставимо в р-ня (1) Згрупуємо 1 та 3 дщоданки Обер. за ф-ю частк. розв. р-ня 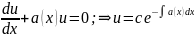. Оберемо з цих розв’язків

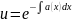
Підст. знайд. ф-ю в ост. р-ня одерж.

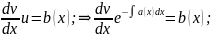
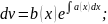
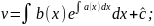
Тоді _{загал розв неоднор р-ня(1).}

4.Однорідні диференціальні рівняння та рівняння, що зводяться до однорідних

Озн. Ф-ю називають однорідною ф-єю мулевого степення, якщо для справдж. рівність

Озн. Однорідн. назив р-ня виду 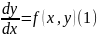якщо ф-я є однорідною ф-єю. нулев. степення.

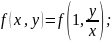
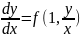; введ. заміну змінної 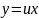, де - х≠0. 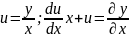; одерж. р-ня є р-ням з відокр. змін. ;

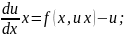
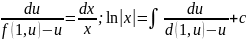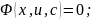
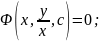
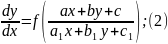
Розв. р-ня: - дійсні числа

1⁰ здійснимо заміну змінної

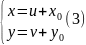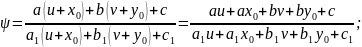
; тоді 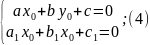Одерж. Сист р-нь,. така с-ма має єдин. розв. якщо її детермінант відмінний від 0. знаход. розв. с-ми (4) і підстав. його в заміну (3). тоді р-ня (2) набув. виду 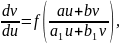одерж. р-ня є однорідн.

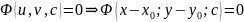його розв.

2⁰

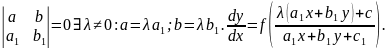
Зробимо заміну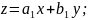

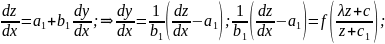- з відокр. змінними.

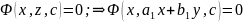; його розв.