1. Теореми про існування та єдиність розв’язків. Задача Коші.

2. Лінійні рівняння першого порядку. Методи Лагранжа та Бернуллі.

3. Рівняння в повних диференціалах.

4. Однорідні диференціальні рівняння та рівняння, що зводяться до однорідних.

5. Рівняння, що не розв’язані відносно похідної. Рівняння Лагранжа та Клеро.

6. Лінійні рівняння n-го порядку. Фундаментальна система розв’язків однорідного рівняння.

Детермінант Вронського. Загальний розв’язок.

7. Лінійні рівняння n-го порядку з сталими коефіцієнтами.

1.Теореми про існування та єдність розв’язків задачі Коші

Рівняння виду – р-ня 1-го порядку. Будем вваж., що його можн. розв. відн. похідної. (1)- ф-я визн. в обл. з пр-ру R²

Озн. Ф-ю назив. розв. р-ня (1) на. (a,b)⊂R². Якщо на ньому вона диф. причому .

Прип. що для точки існ. розв. р-ня(1) , і що. .Числа х₀,у₀ наз початков.значен,а умову початк умовою..Довед. єдність цього розв. Прип. що ще розв’язок р-ня (1) визнач. на інтервалі , що . Якщо на то говорять, що розв. за знач. x₀, y₀ єдиний.

Озн. Розвязок називається частк. розв. р-ня(1). Ф-ю , де c-числовий параметр наз. загальн. розв. р-ня (1), якщо будь-який його част. розв. одерж. від заг. при деякому частк. знач. Параметра с.

Озн. Р-ть. називають частковим інтегралом р-ня (1) якщо вона неявн. визн. част. розв. цього р-ня. Загальн. інтегр. р-ня (1) назив. співвідн. яке визн. неявно заг. розв. р-ня(1).Графіек розв р-ня наз інтегральною кривою.Точку(х₀,у₀) наз.особливою для р-ня(1),якщо через неї проходить більше однієї інтегр.кривої.

Озн. Розв р-ня(1),який визнач інтегр криву,що складається лише з особливих точок,наз.особливим розв.

Т.Пеано Якщо ф-я f(x,y)неп на Г за сукупність змінних,то для будь-якої т(х₀,у₀)з Г існує розв. р-ня(1)з початк знач.х₀,у_0., , що = у₀

Задача Коші.

1.знайти частк. розв. р-ня (1) який визнач. початковою умовою .

2.вияснити чи він єдиний.

Т.Пікара нехай виконуються умови т.Пеано, і до того ж задовольняє умови Ліпшеца відносно у тобто для (х,у) є Г виконується нерівність , тоді розвязок про який йде мова в теоремі Пеано єдиний.

Дов. Зведемо розв’язання задачі Коші до відшукання розв’язку деякого інтегрального рівняння , х₀,у₀ є Г . Розглянемо інтегральне рівняння (2). Надалі будем шукати розвязок р-ня (2) він і є розв’язком поставленої задачі Коші.

Нехай множина G містить в собі точку (х₀,у₀) і є замкненою GсГ, тоді функція обмежена на множині G оскільки вона на ній неперервна, це значить, що існує таке число k, що , (х,у)є G. Підберемо число h таким чином, щоб кожна точка (х,у) для якої і крім того, щоб 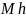було строго менше 1. 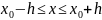позначимо Н. . Р

Розглянемо множину елементами якої є неперервні функції від х виду , які мають таку властивість при при хєН . Очевидно, що с С_н. З мат. аналізу відомо, що С_н є повним метричним простором в якому відстань задається формулою . Оскільки є підмножиною С_н то ця множина утворює повний метричний простір з цією відстаню при умові, що ця множина замкнена. Покажемо, що - замкнена. Для цього досить показати , що вона містить всі свої граничні точки. Припустимо, що є граничною точкою . Тоді в множині . Це значить,що nєN . В останній рівності перейдемо до границі. , тому . Отже множина

Означимо відображення А, що діє на елементи простору таким чином , покажемо, що це відображення є відображенням стиску, що А: . Крім того /

Нехай тоді . За означенням стискаючого оператора робимо висновок, що А- є оператором стиску. Оскільки він діє в повному метричному просторі то для нього існує нерухома точка , а це значить = , а це значить , отже