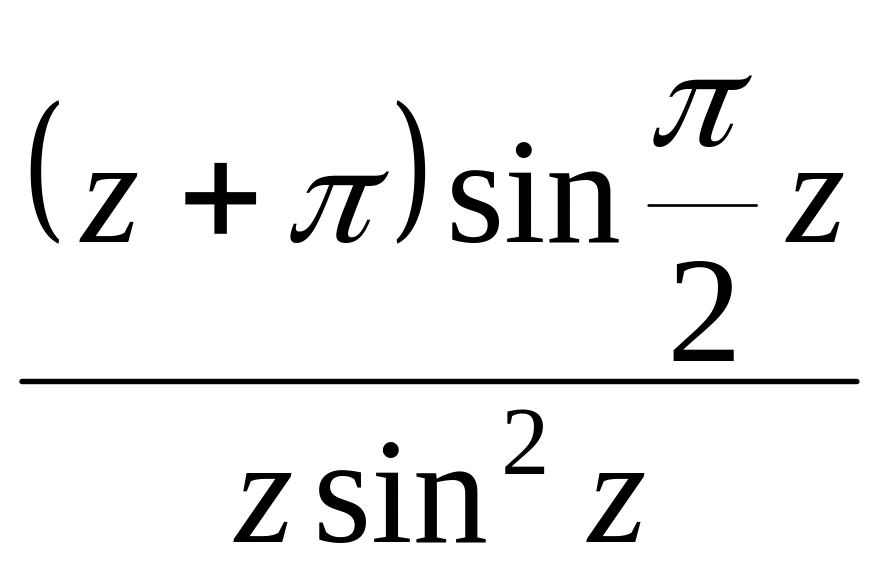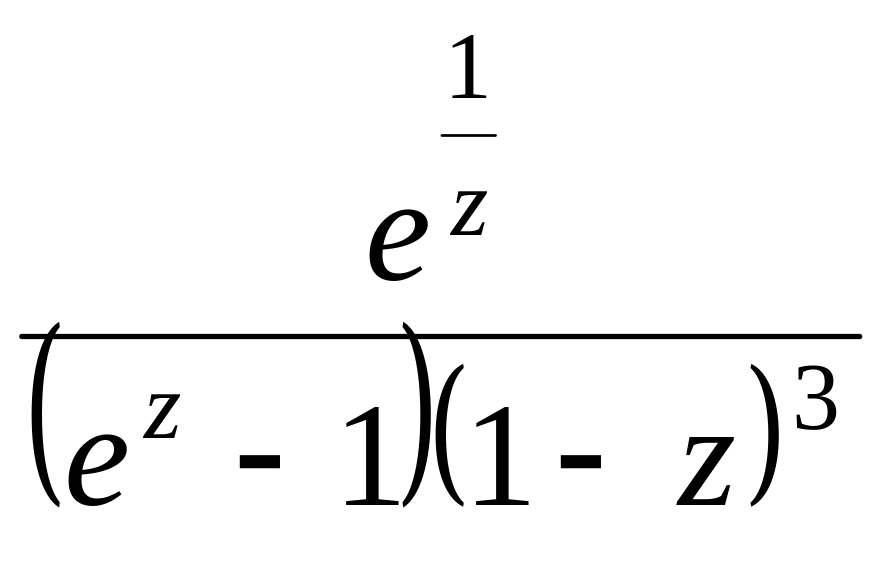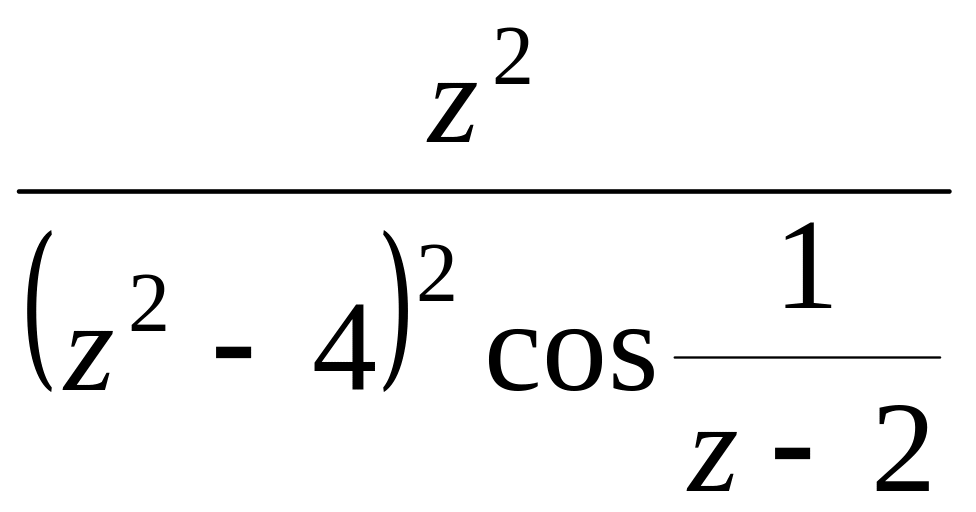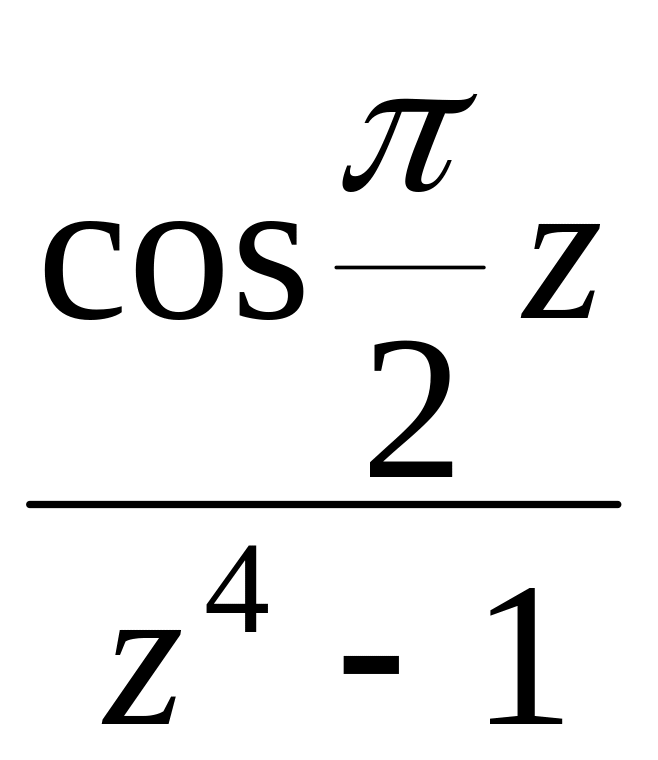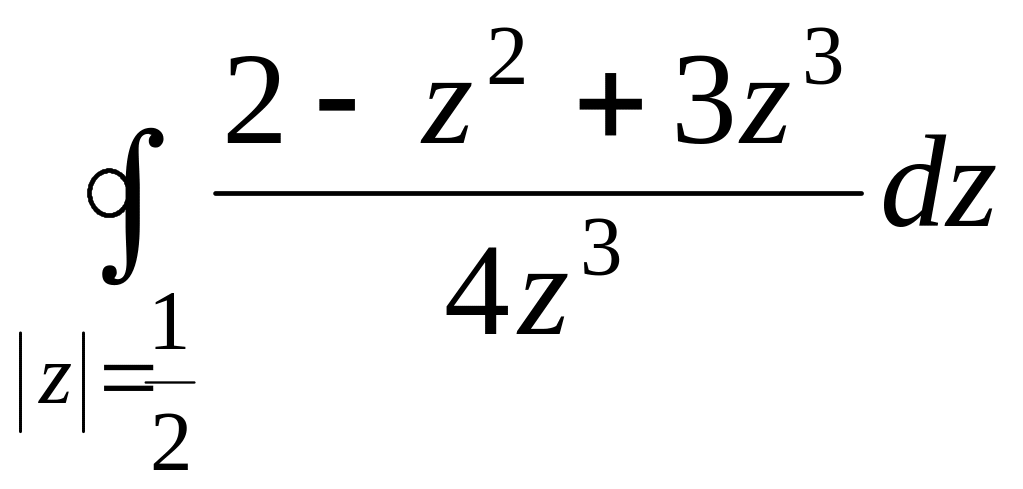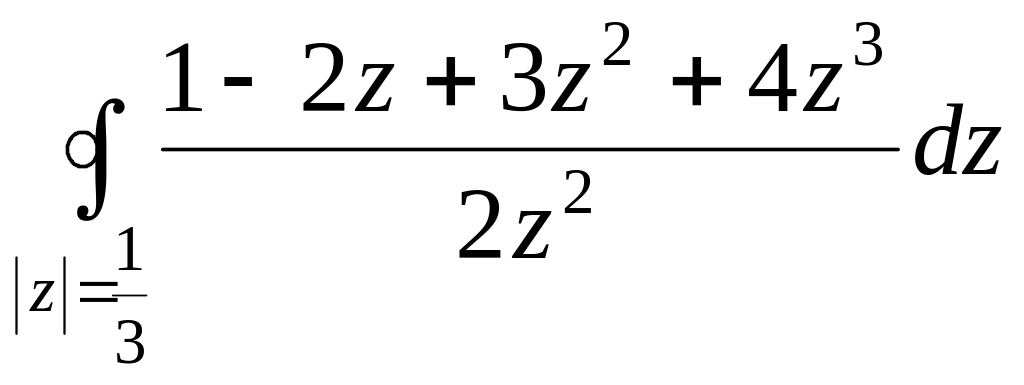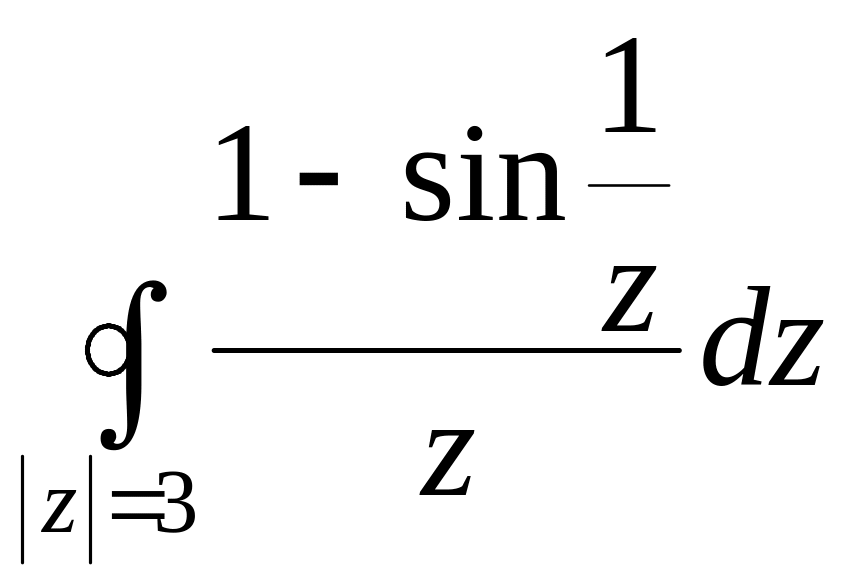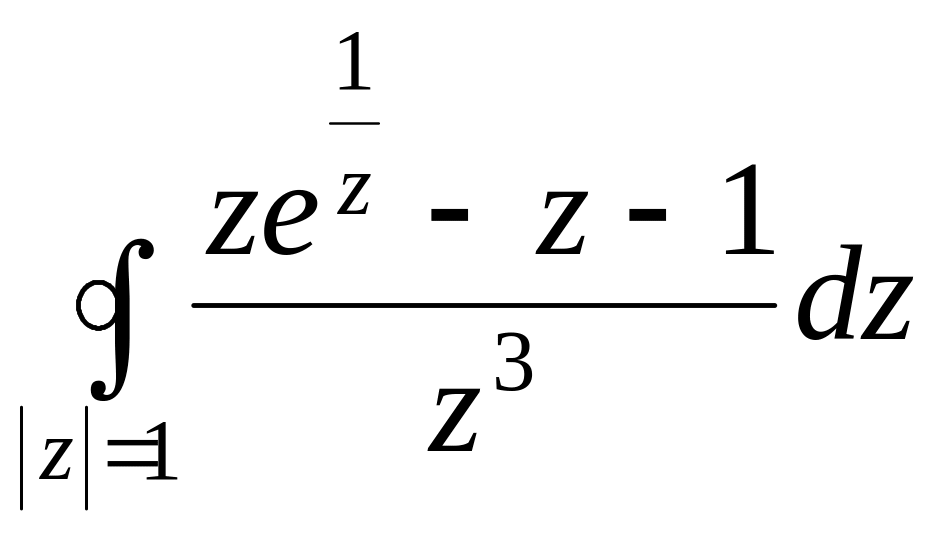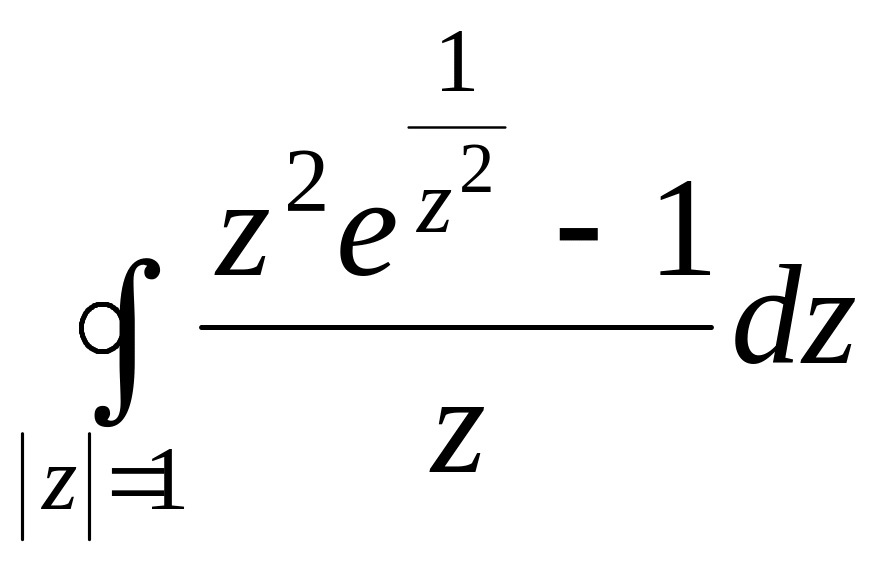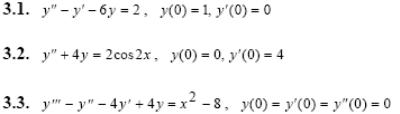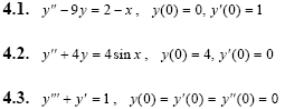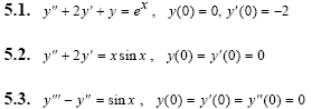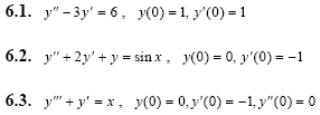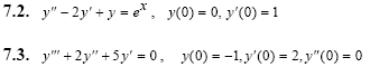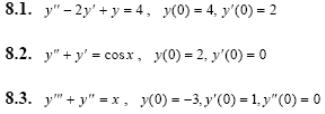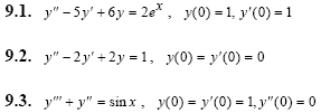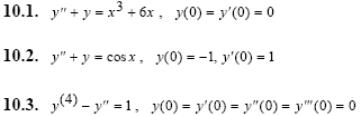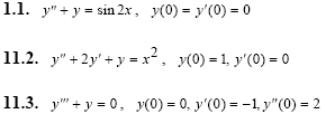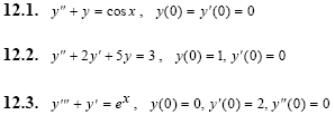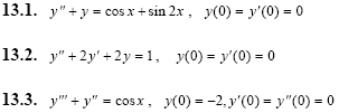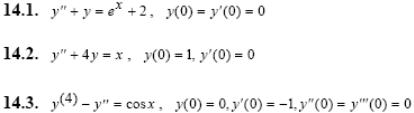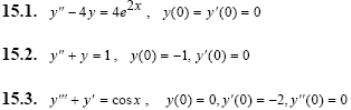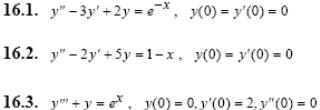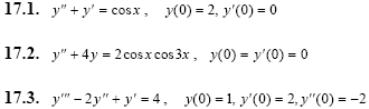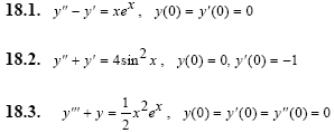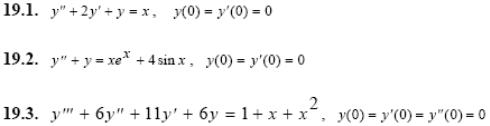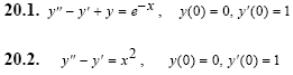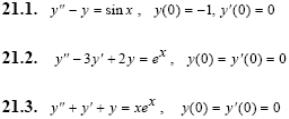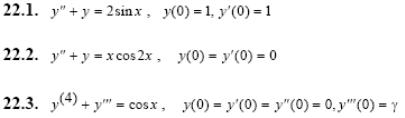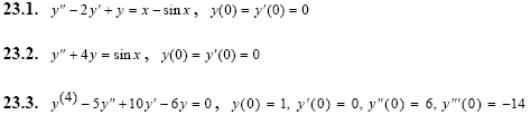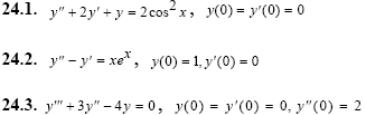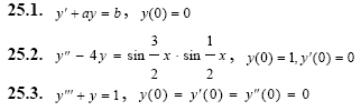- •Идз 1. Кратные интегралы Задача 1. Построить область интегрирования. Изменить порядок интегрирования.
- •Задача 2. Построить область интегрирования, вычислить двойной интеграл.
- •Задача 3. Построить область интегрирования. Вычислить интеграл.
- •Задача 4. Построить область интегрирования. Вычислить интеграл.
- •Задача 5. Найти площадь фигуры, ограниченной данными линиями (7).
- •Задача 6. Пластинка d задана неравенствами, - поверхностная плотность. Построить изображение пластины. Найти массу пластинки. (9)
- •Задача 7. Найти объем тела, заданного ограничивающими его поверхностями. (11)
- •Задача 8. Найти объем тела, заданного ограничивающими его поверхностями. (13)
- •Задача 9. Тело V задано ограничивающими его поверхностями, - плотность. Найти массу тела. (16)
- •Идз 2. Скалярные и векторные поля. Криволинейные интегралы Задача 1.
- •Задача 2. Найти векторные линии в векторном поле . Построить векторные линии в окрестности начала координат.
- •Задача 3. Вычислить данные криволинейные интегралы первого рода. Построить кривую l, указать направление интегрирования.
- •Задача 4. Вычислить данные криволинейные интегралы первого рода. Построить кривую l
- •Задача 5. Найти криволинейный интеграл второго рода векторного поля вдоль контура (в направлении, соответствующем возрастанию параметра ). Сделать чертеж контура.
- •Задача 6. Найти модуль циркуляции векторного поля вдоль контура .
- •Задача 7. С использованием криволинейных интегралов решить следующие задачи. Сделать иллюстрацию.
- •Идз 3. Поверхностные интегралы и теория поля Задача 1. Найти поверхностный интеграл первого рода по поверхности s, где s - часть плоскости (p), отсеченная координатными плоскостями (257 - 2)
- •Задача 2. Вычислить массу полусферы , если поверхностная плотность в каждой ее точке
- •Задача 4. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя). Сделать чертеж поверхности
- •Задача 7. Найти наибольшую плотность циркуляции векторного поля в точке (273)
- •Задача 8. Проверить является ли векторное поле потенциальным и соленоидальным. В случае потенциальности поля найти его потенциал.
- •Задача 2. Для данной функции найти изолированные особые точки и определить их тип
- •Задача 3. Вычислить интеграл, построить область интегрирования и отметить особые точки подынтегральной функции.
- •Задача 4. Найти оригинал по заданному изображению
- •Задача 5. Решить дифференциальные уравнения с начальными условиями (задача Коши) операционным методом.
- •Образец титульного листа
- •Индивидуальное домашнее задание по высшей математике Название
Задача 2. Для данной функции найти изолированные особые точки и определить их тип
2.1.
|
2.2.
|
2.3.
|
2.4.
|
2.5.
|
2.6.
|
2.7.
|
2.8.
|
2.9.
|
2.10.
|
2.11.
|
2.12.
|
2.13.
|
2.14.
|
2.15.
|
2.16.
|
2.17.
|
2.18.
|
2.19.
|
2.20.
|
2.21.
|
2.22.
|
2.23.
|
2.24.
|
2.25.
|
2.26.
|
2.27.
|
2.28.
|
2.29.
|
2.30.
|
2.31.
|
|
|
Задача 3. Вычислить интеграл, построить область интегрирования и отметить особые точки подынтегральной функции.
3.1.
|
3.2.
|
3.3.
|
3.4.
|
3.5.
|
3.6.
|
3.7.
|
3.8.
|
3.9.
|
3.10.
|
3.11.
|
3.12.
|
3.13.
|
3.14.
|
3.15.
|
3.16.
|
3.17.
|
3.18.
|
3.19.
|
3.20.
|
3.21.
|
3.22.
|
3.23.
|
3.24.
|
3.25.
|
3.26.
|
3.27.
|
3.28.
|
3.29.
|
3.30.
|
3.31.
|
|
Задача 4. Найти оригинал по заданному изображению
4.1.
|
4.2.
|
4.3.
|
4.4.
|
4.5.
|
4.6.
|
4.7.
|
4.8.
|
4.9.
|
4.10.
|
4.11.
|
4.12.
|
4.13.
|
4.14.
|
4.15.
|
4.16.
|
4.17.
|
4.18.
|
4.19.
|
4.20. |
4.21.
|
4.22.
|
4.23.
|
4.24.
|
4.25.
|
4.26.
|
4.27.
|
4.28.
|
4.29.
|
4.30.
|
4.31.
|
|
Задача 5. Решить дифференциальные уравнения с начальными условиями (задача Коши) операционным методом.
1.1.
1.2.
1.3.
|
2.1.
2.2.
2.3.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Не хватает вариантов |
|
|
|
|
Образец титульного листа
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ
имени академика С.П.КОРОЛЕВА (национальный исследовательский университет)

Кафедра высшей математики