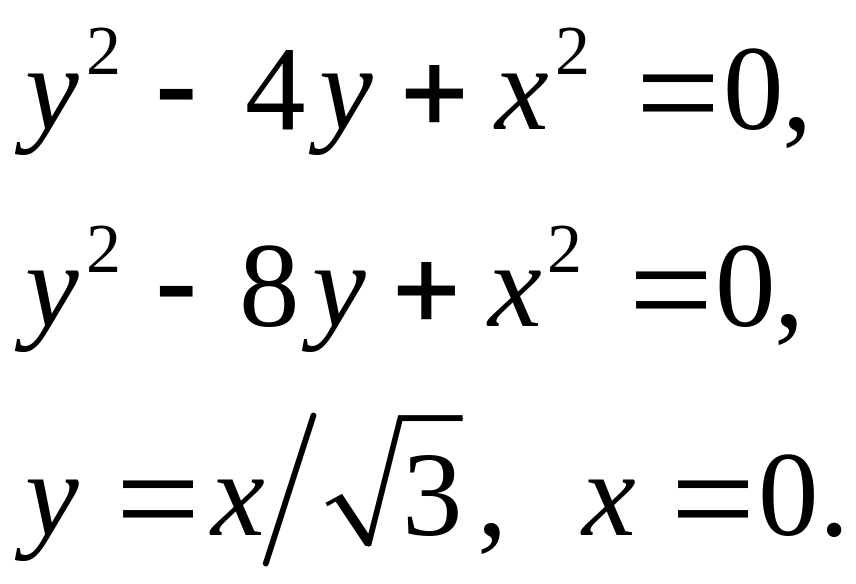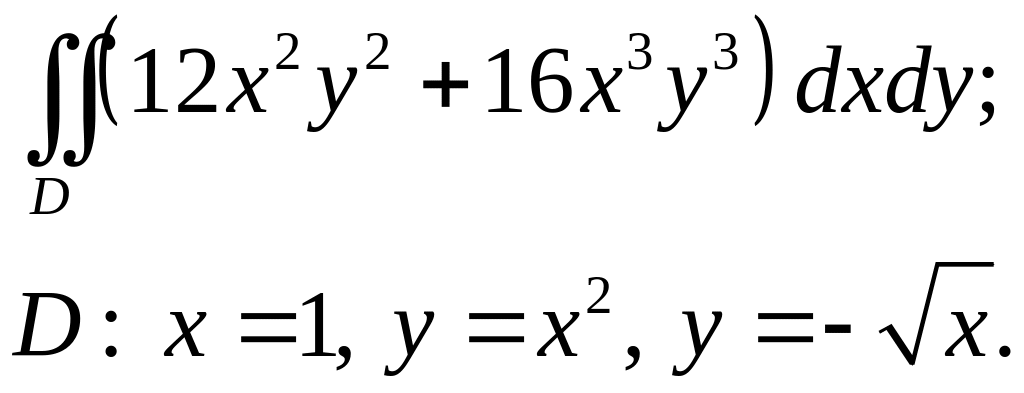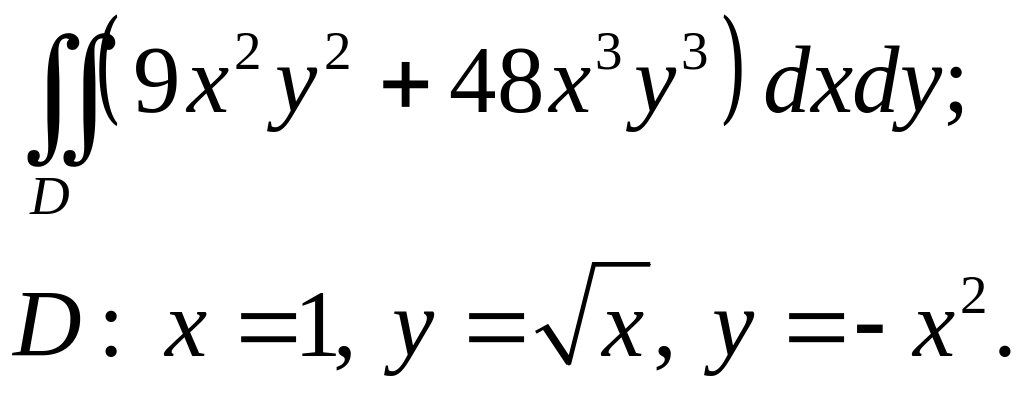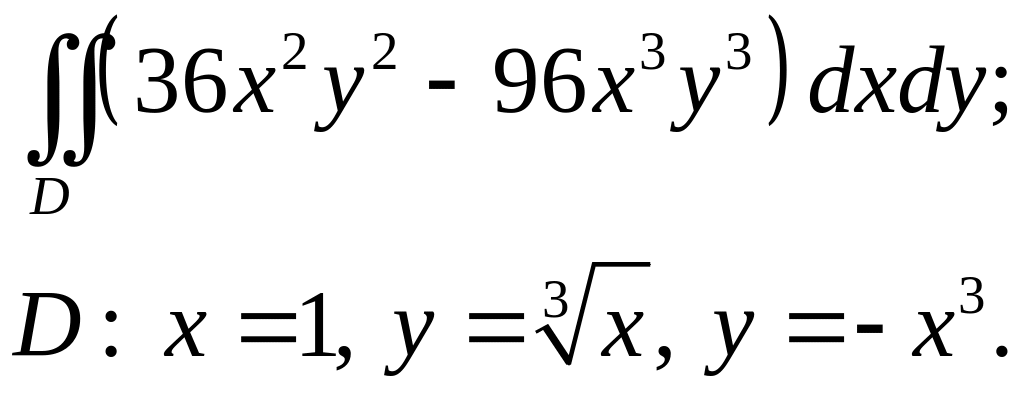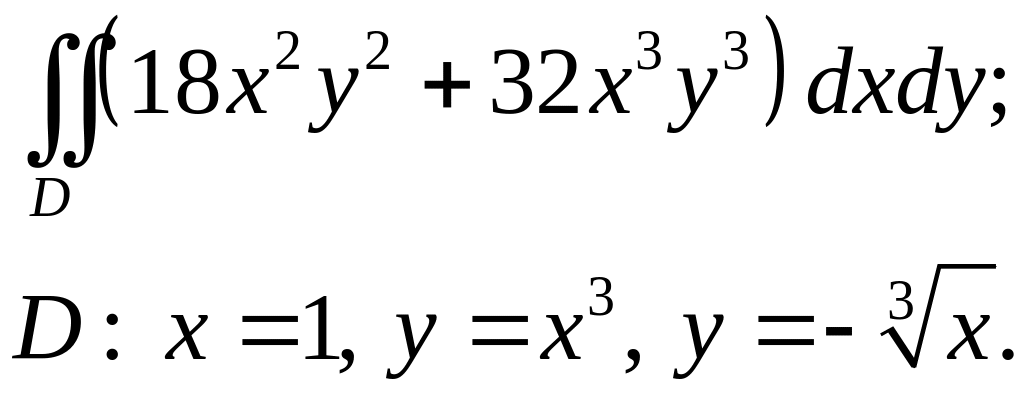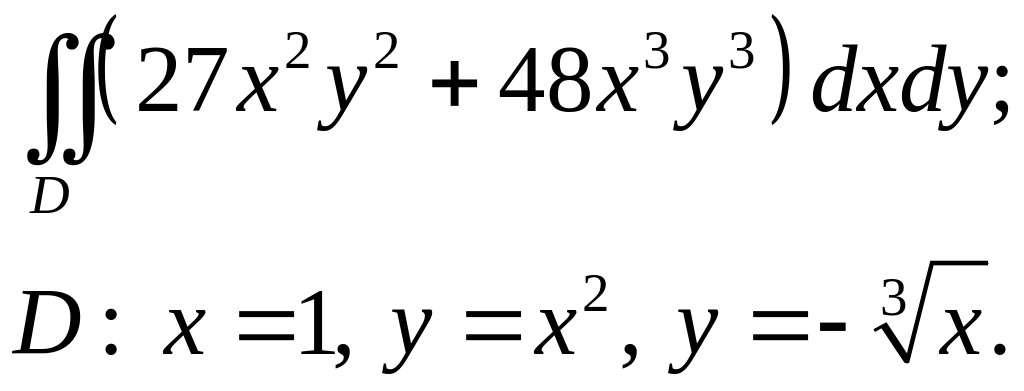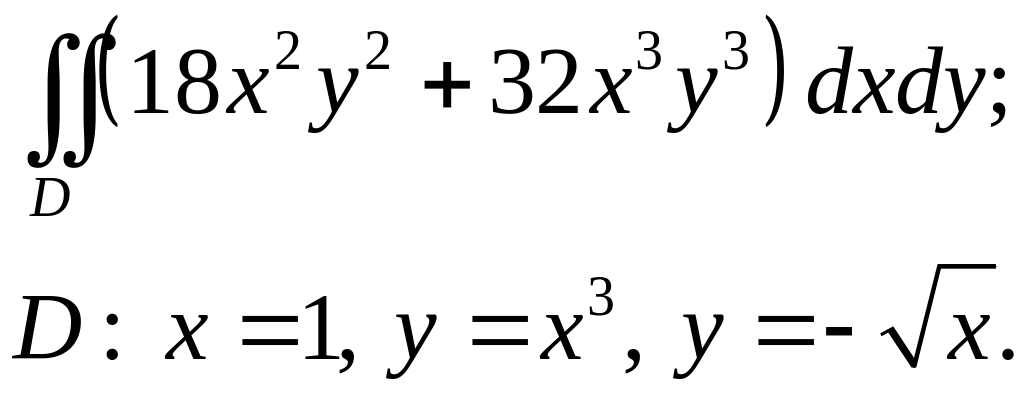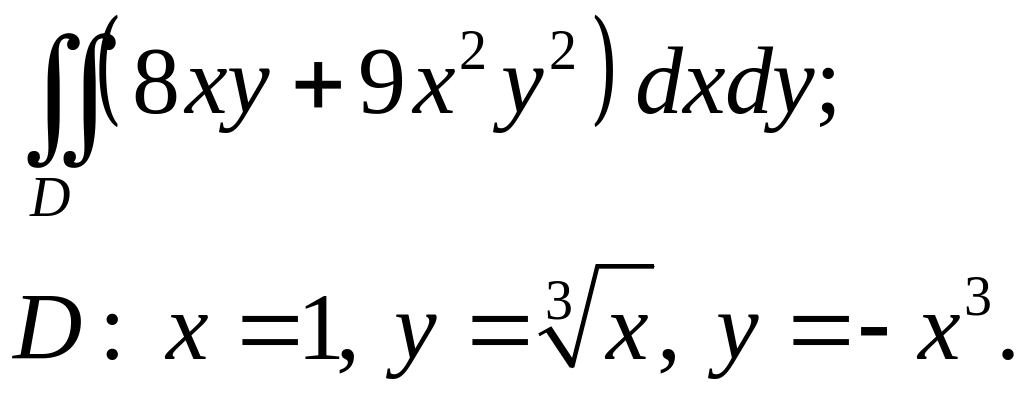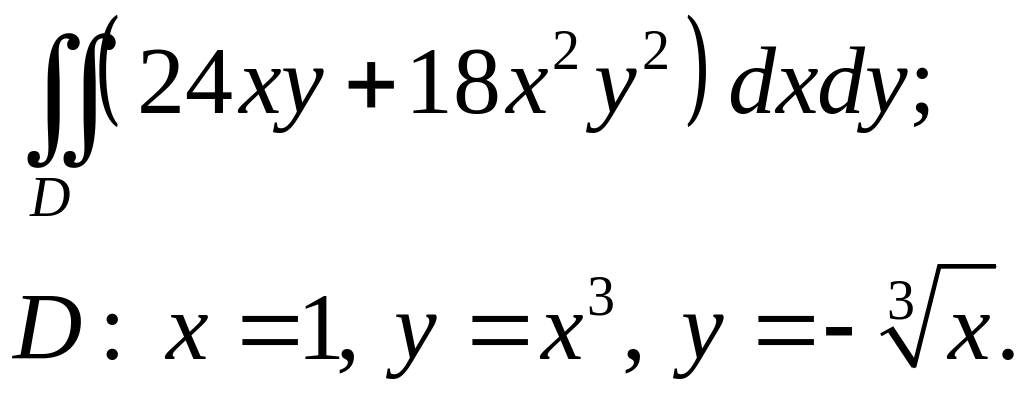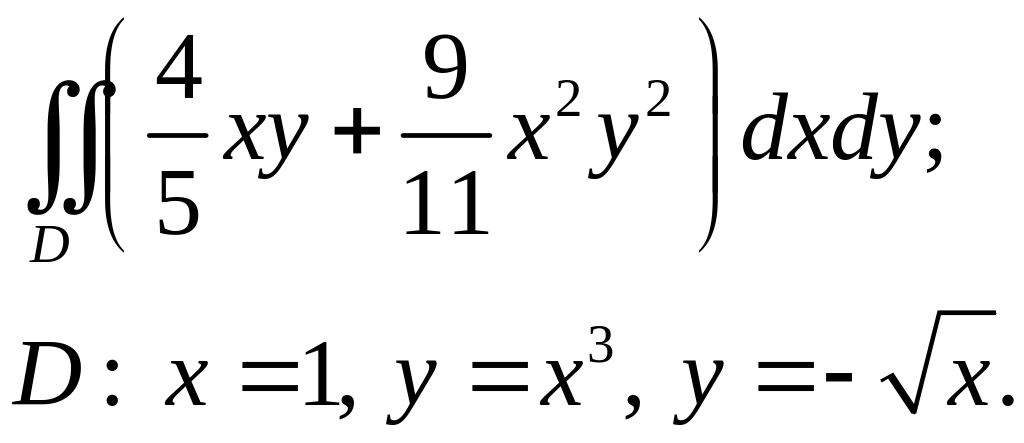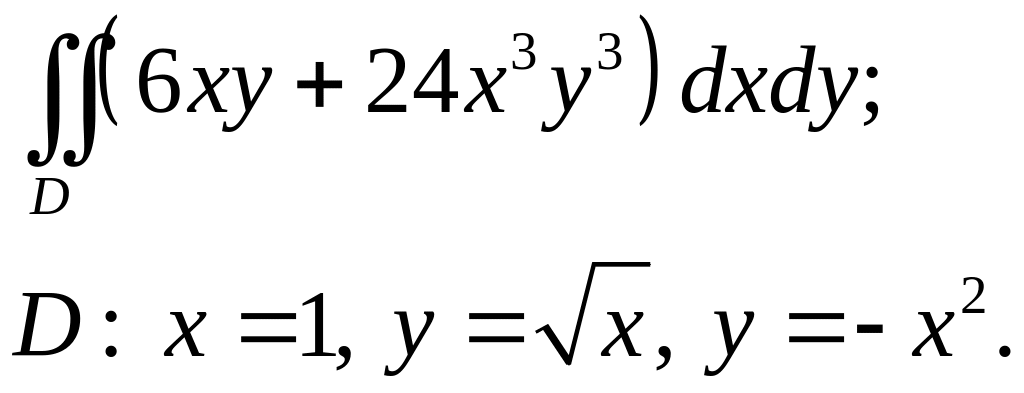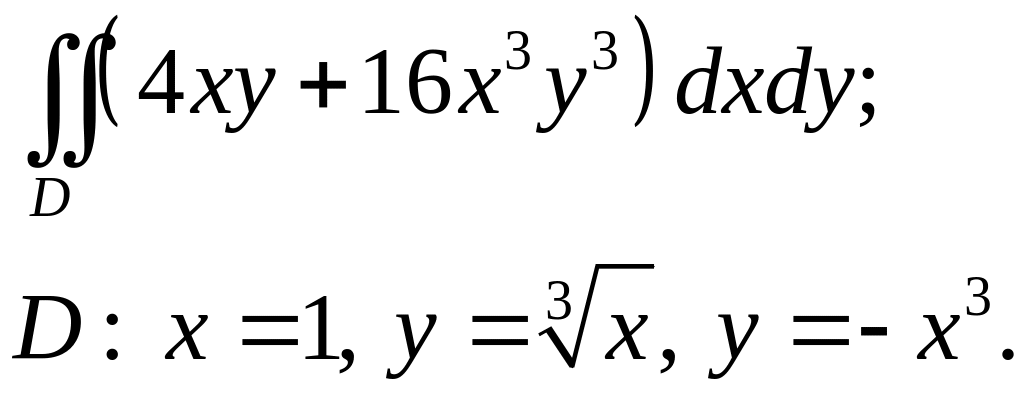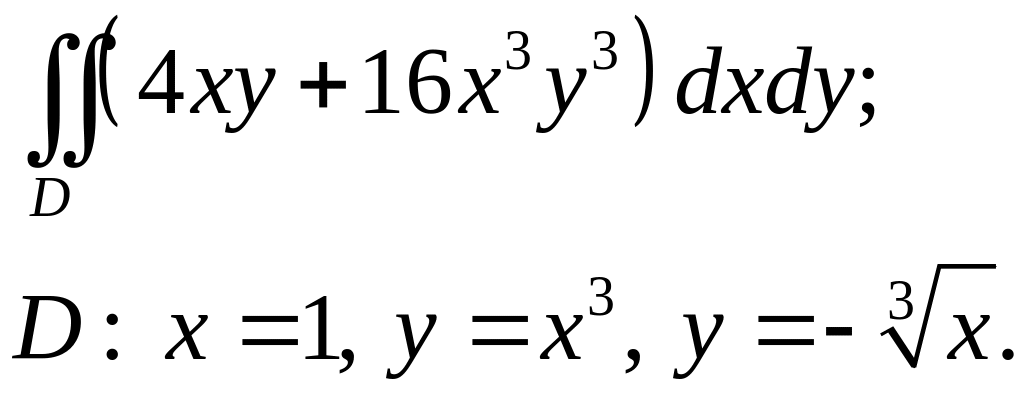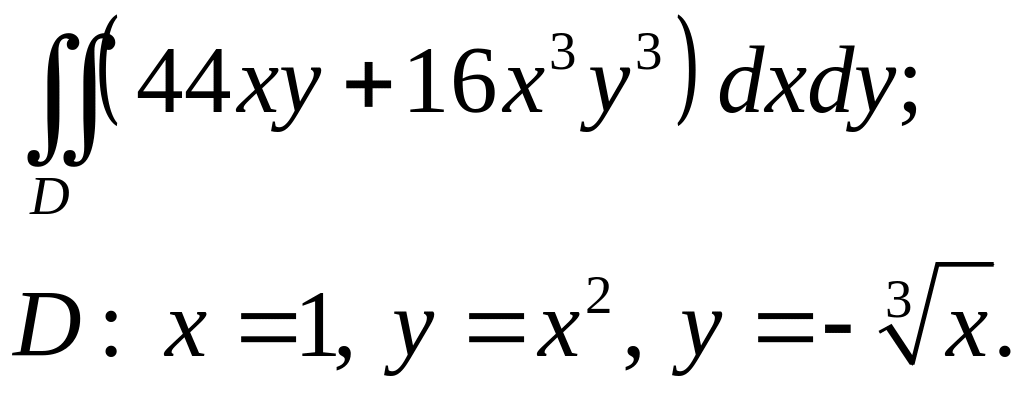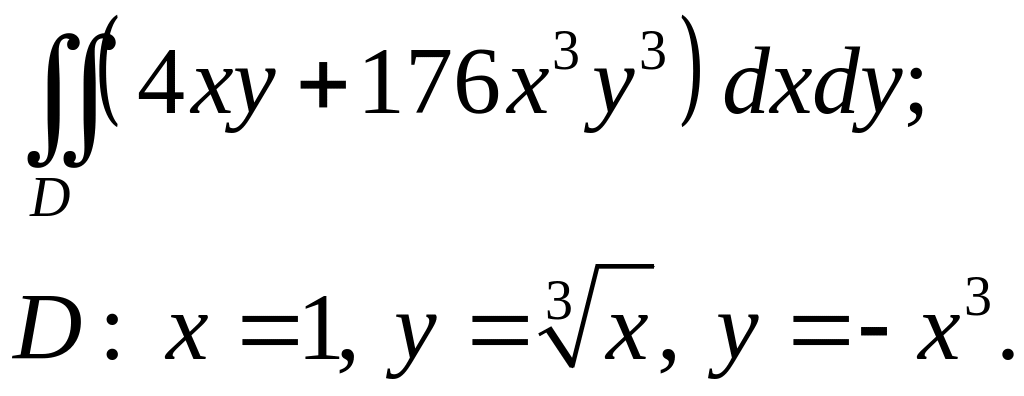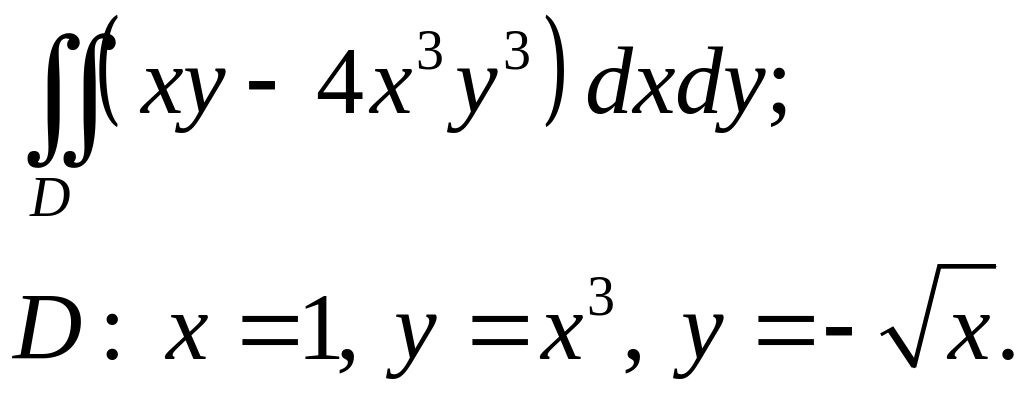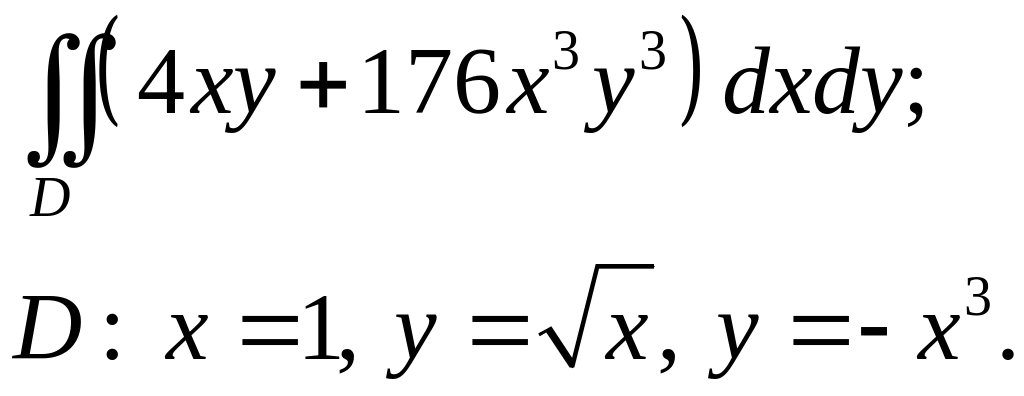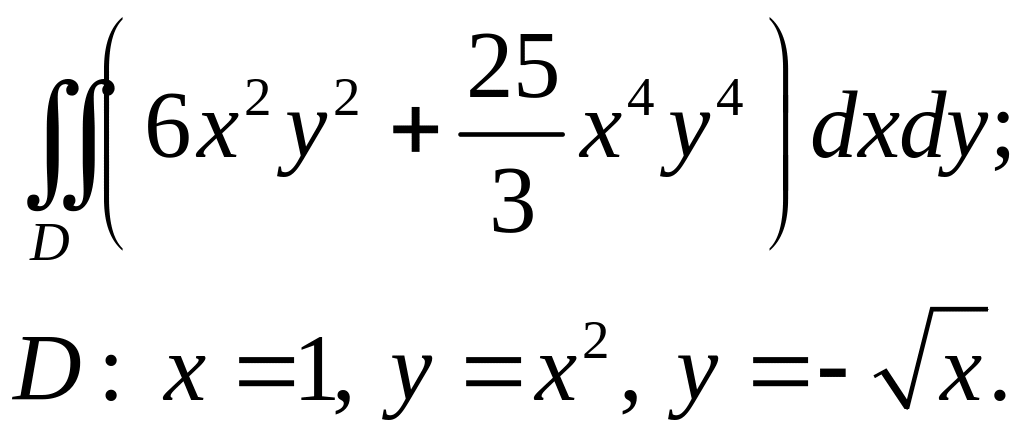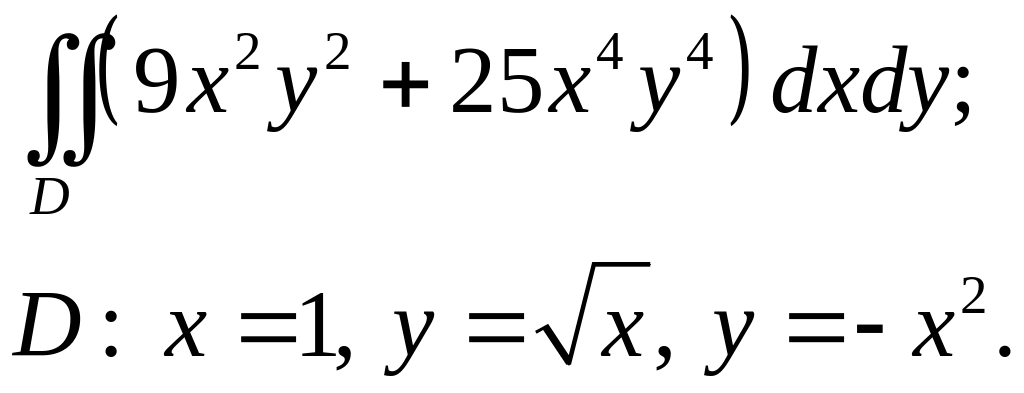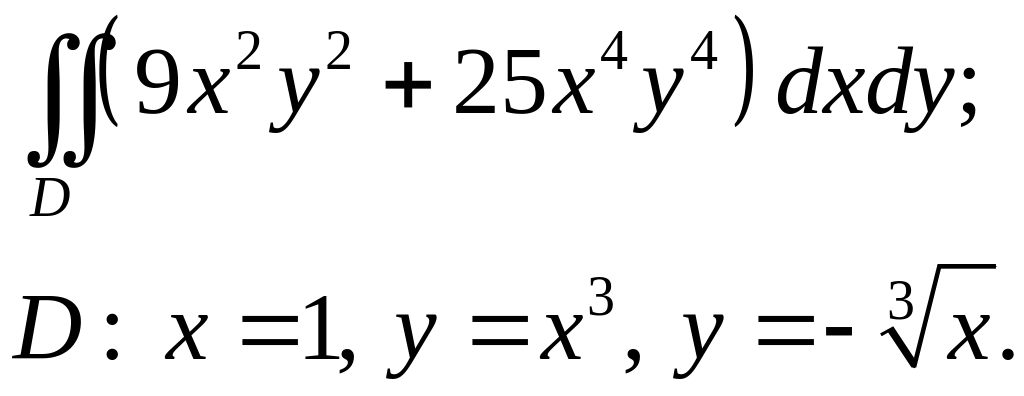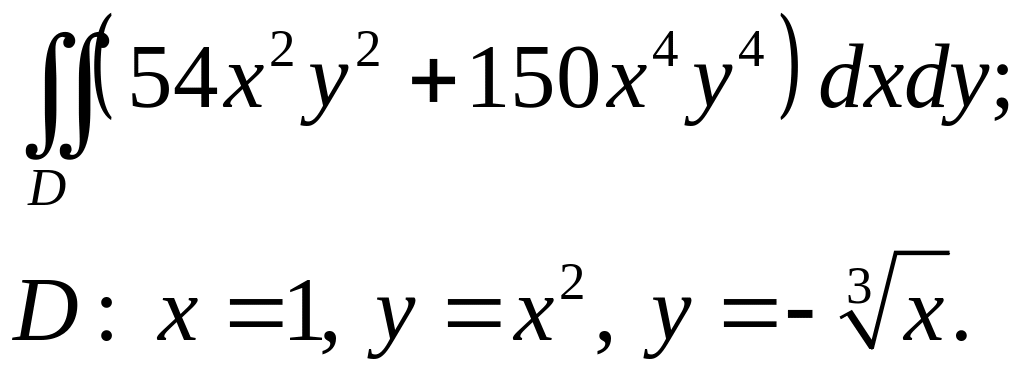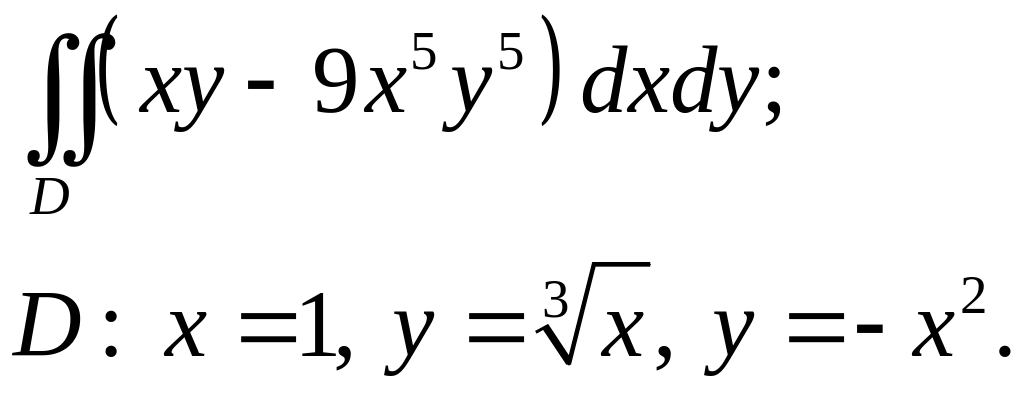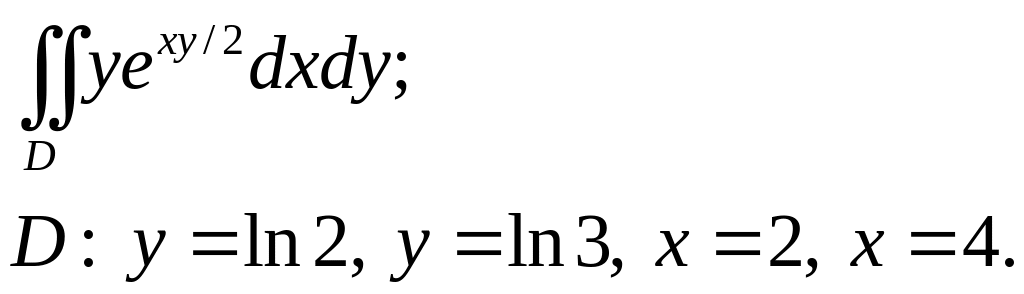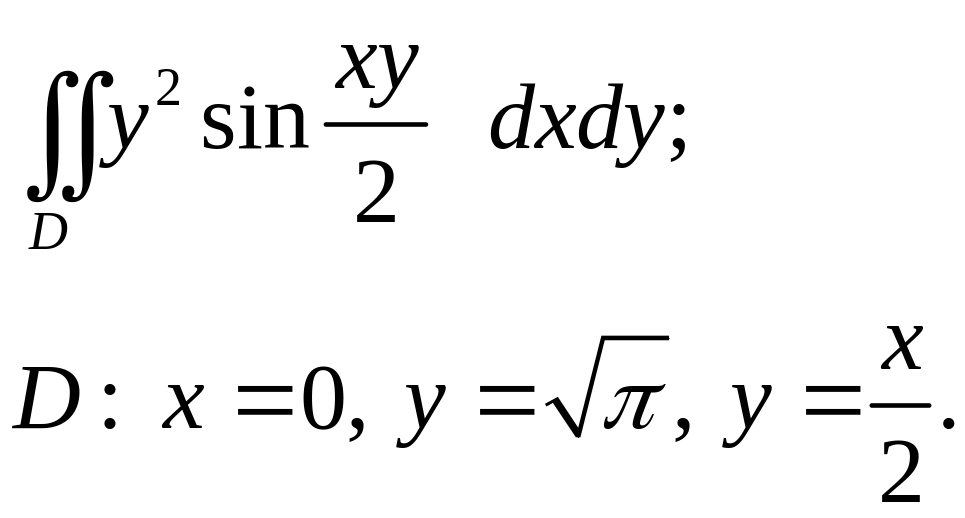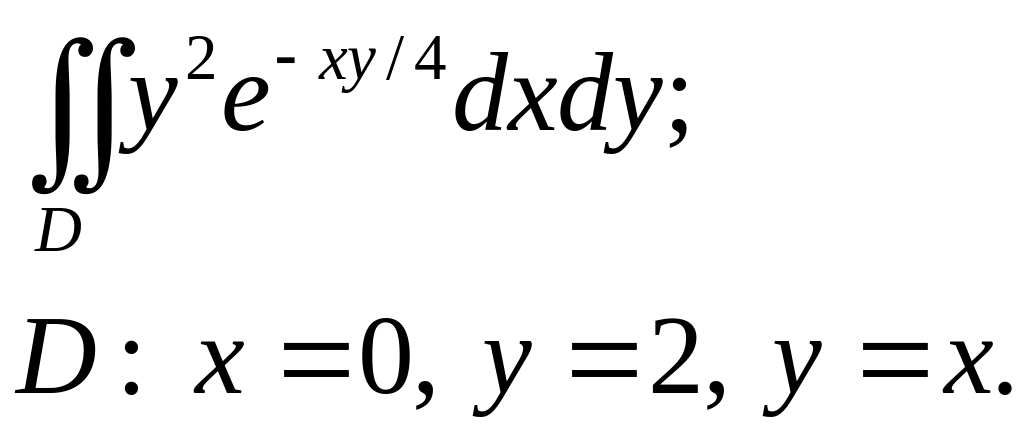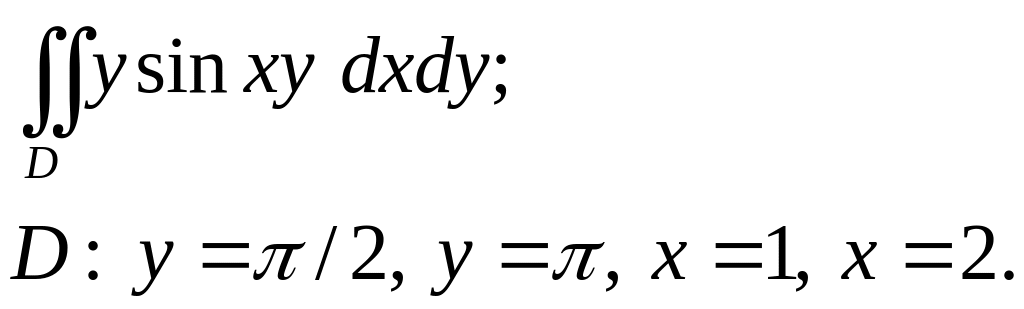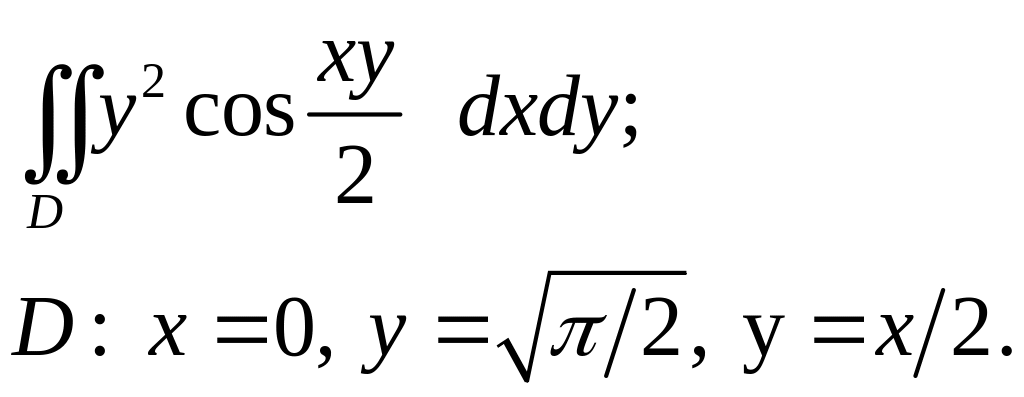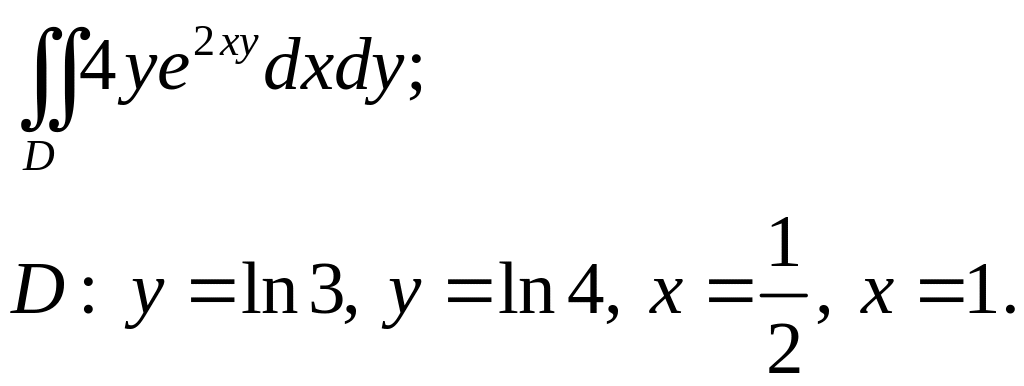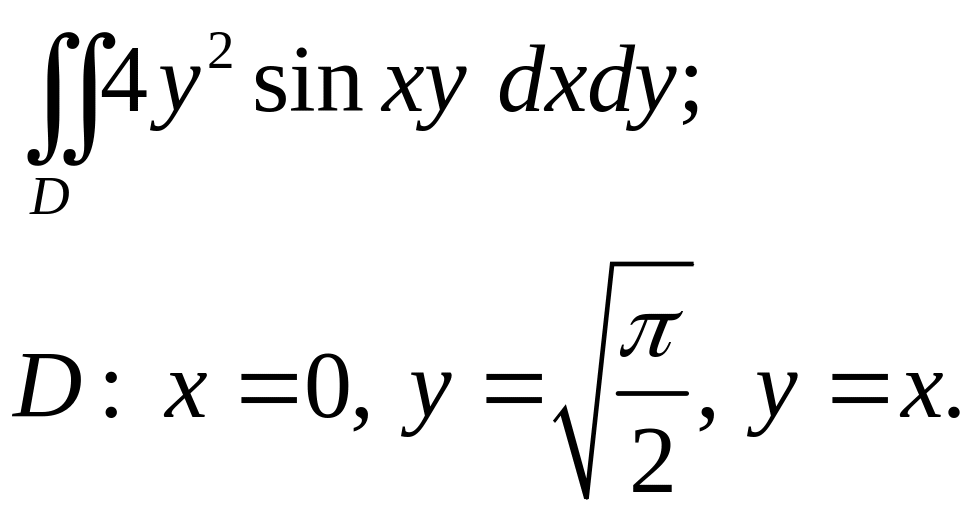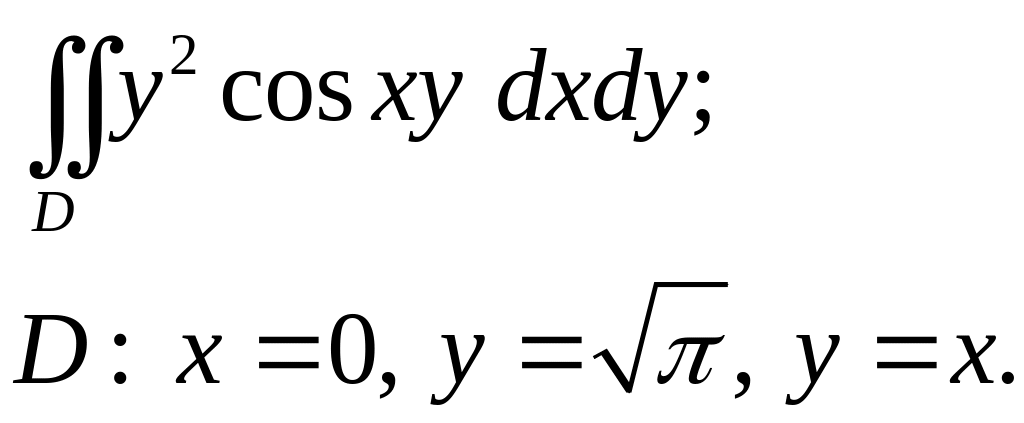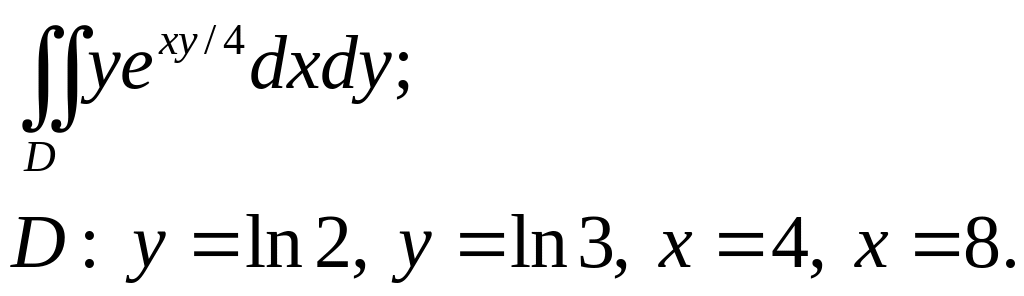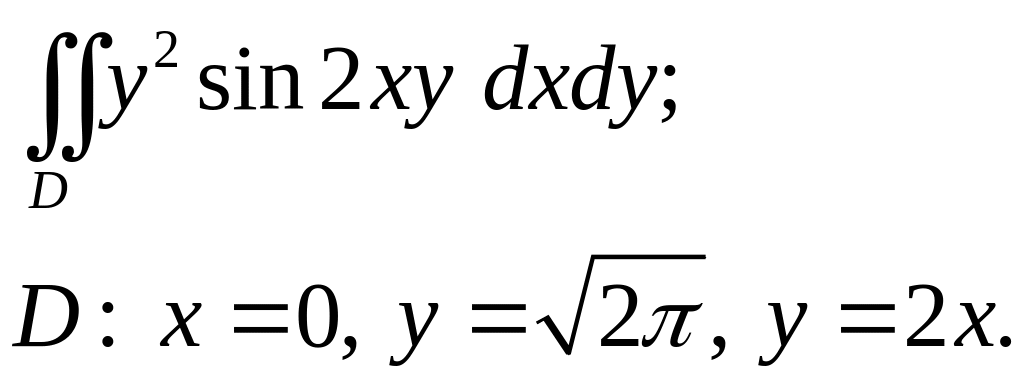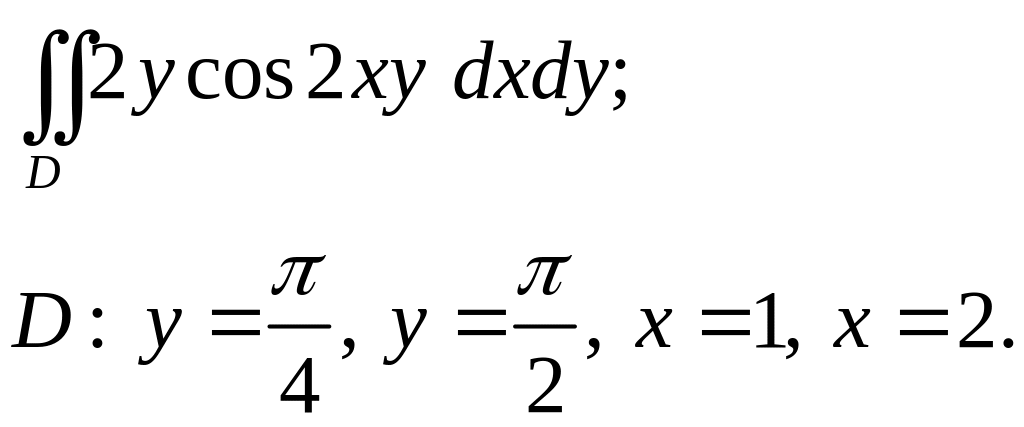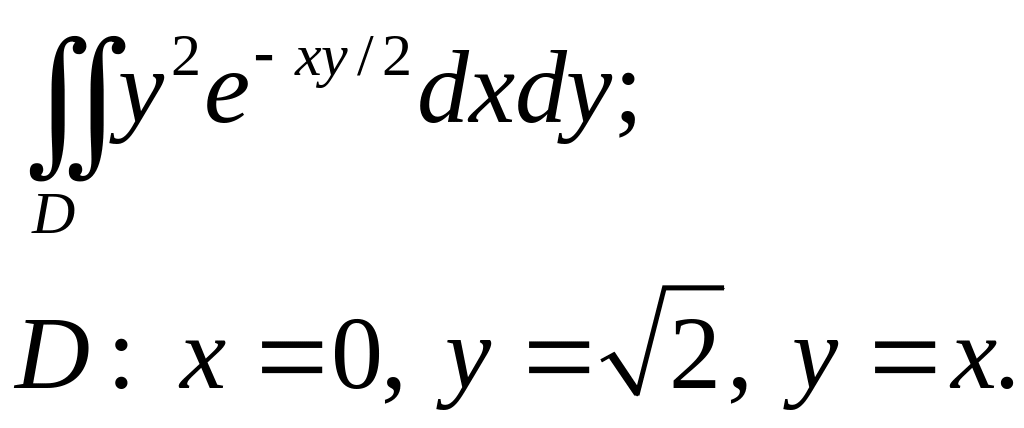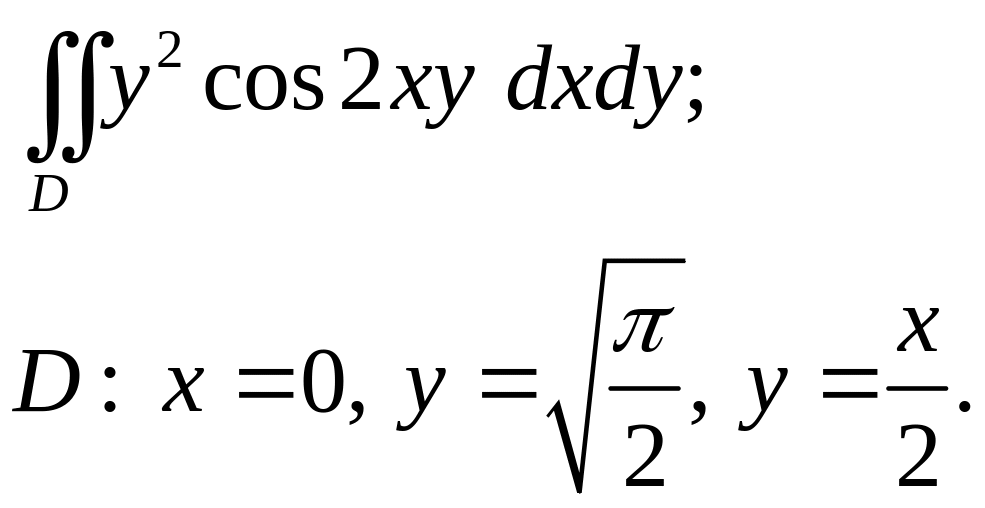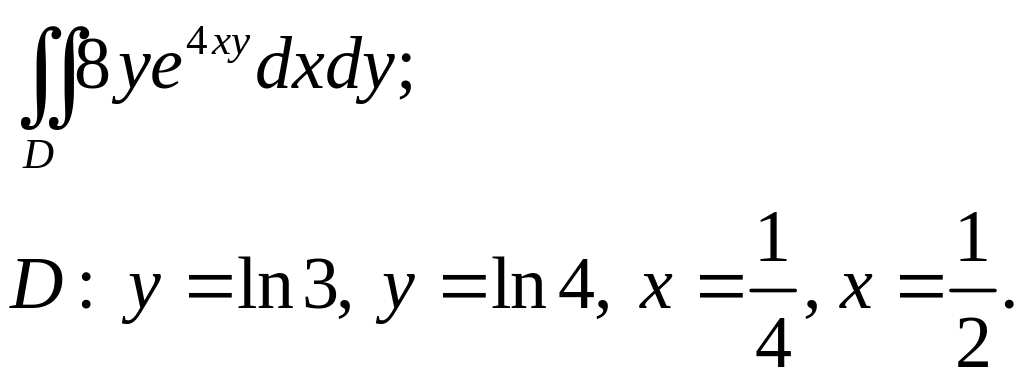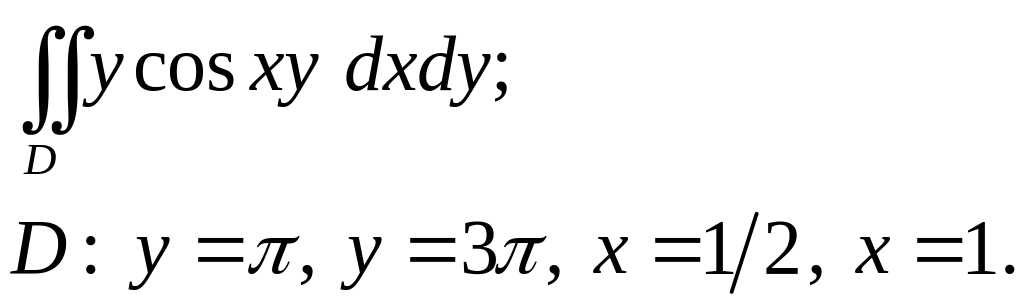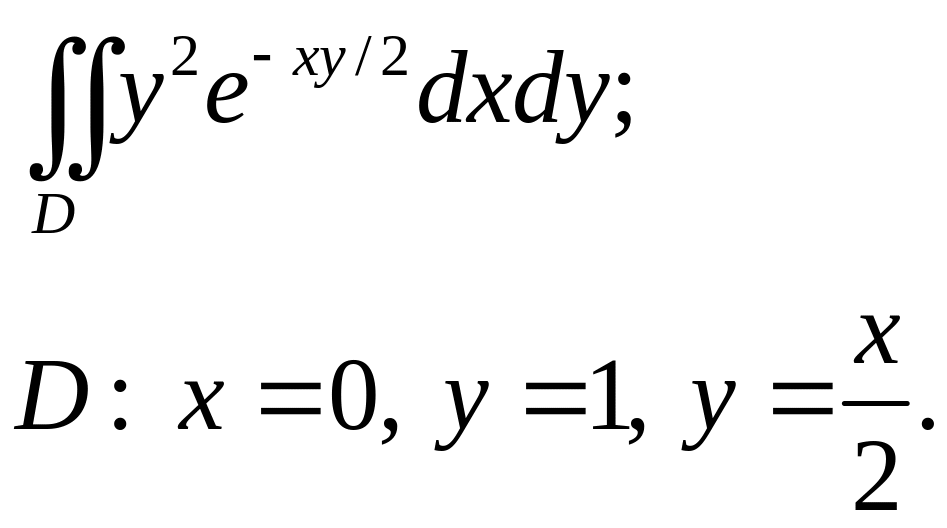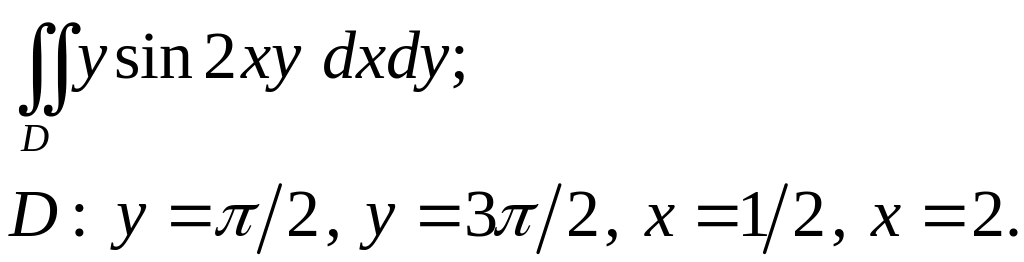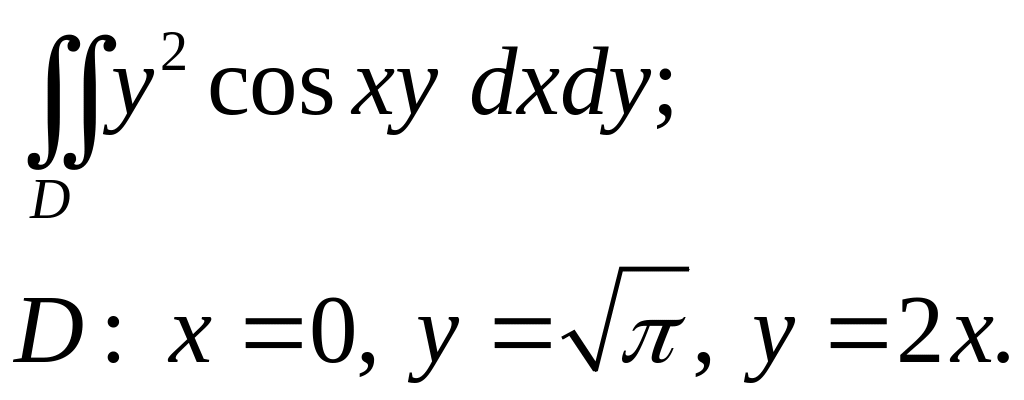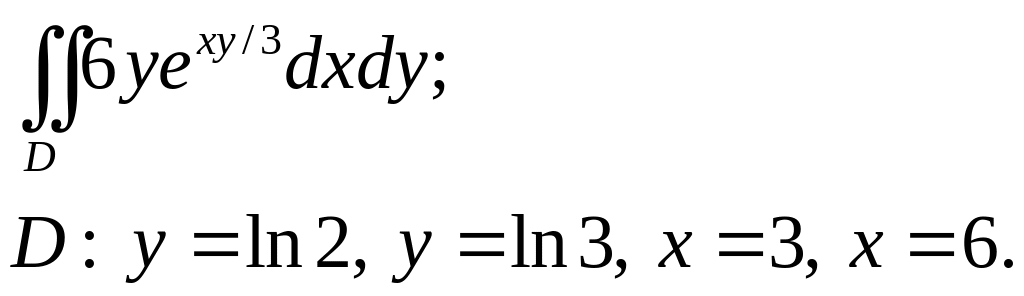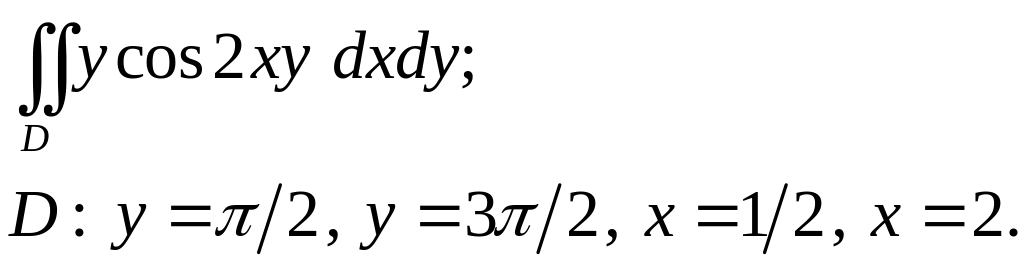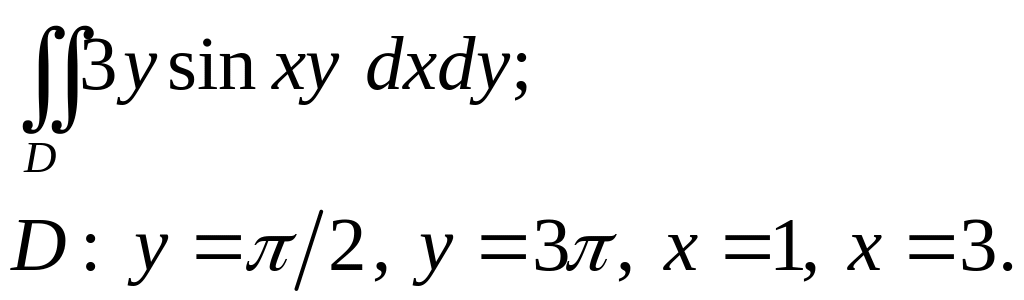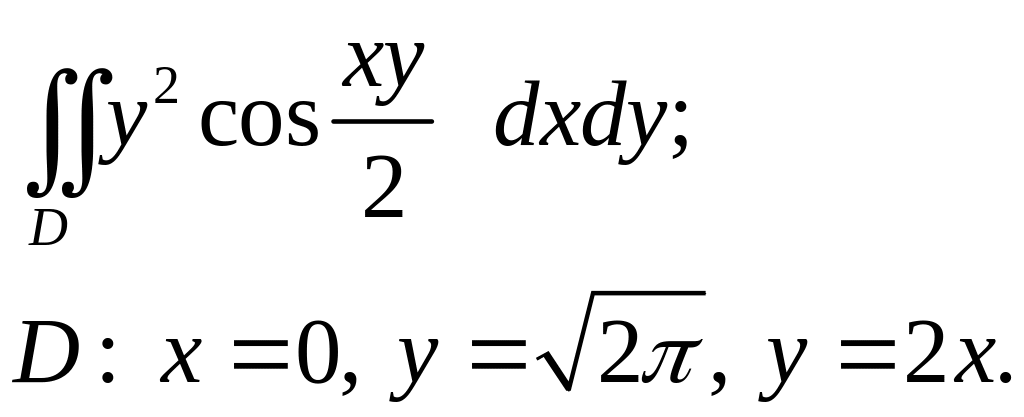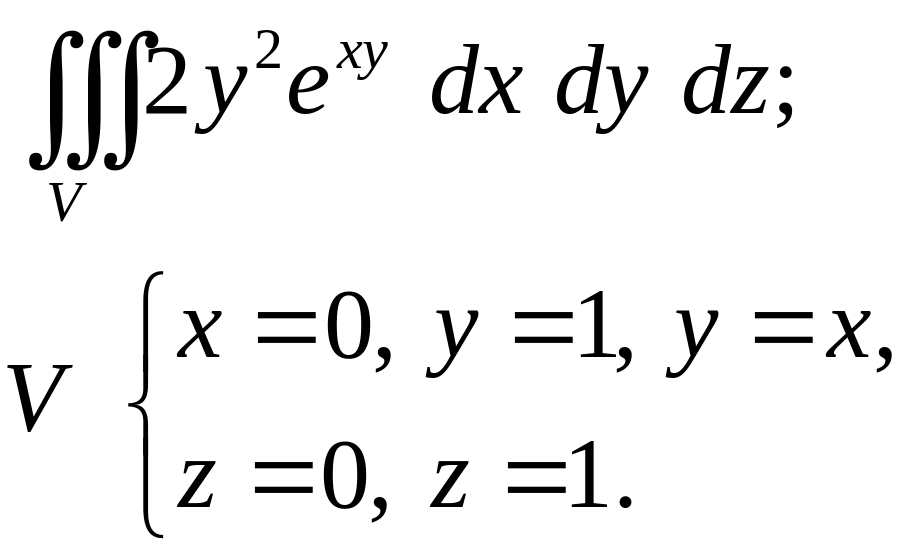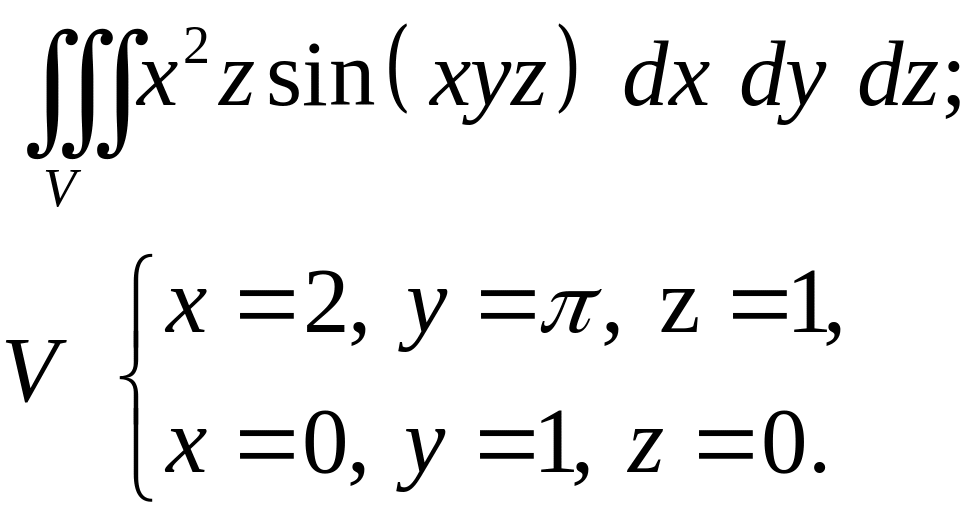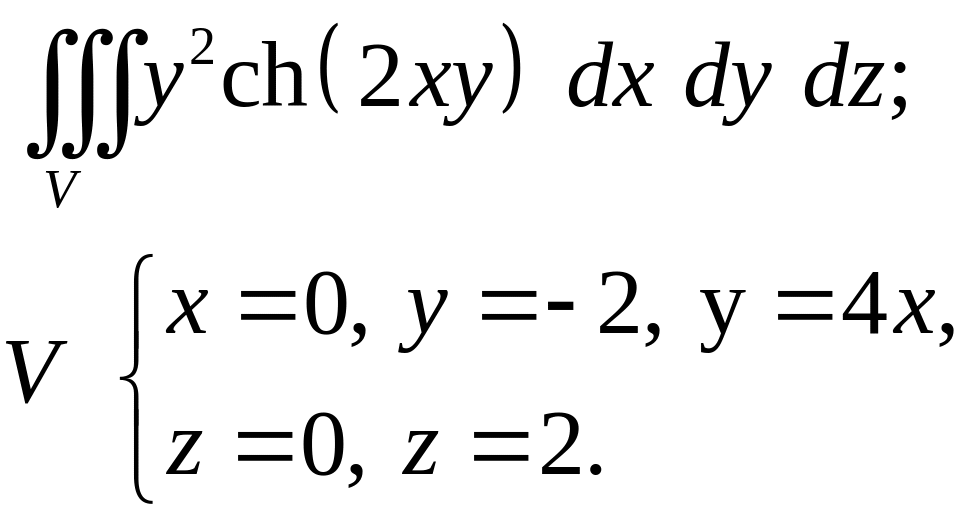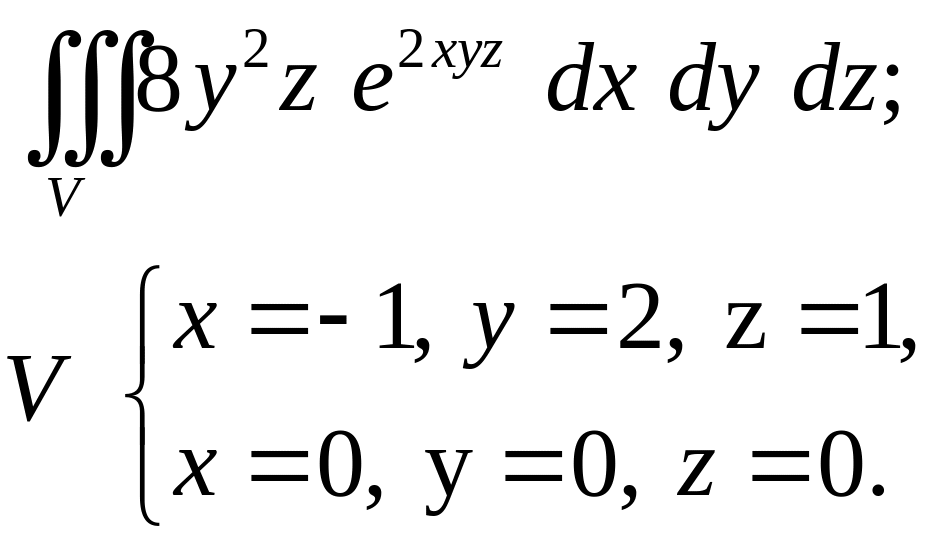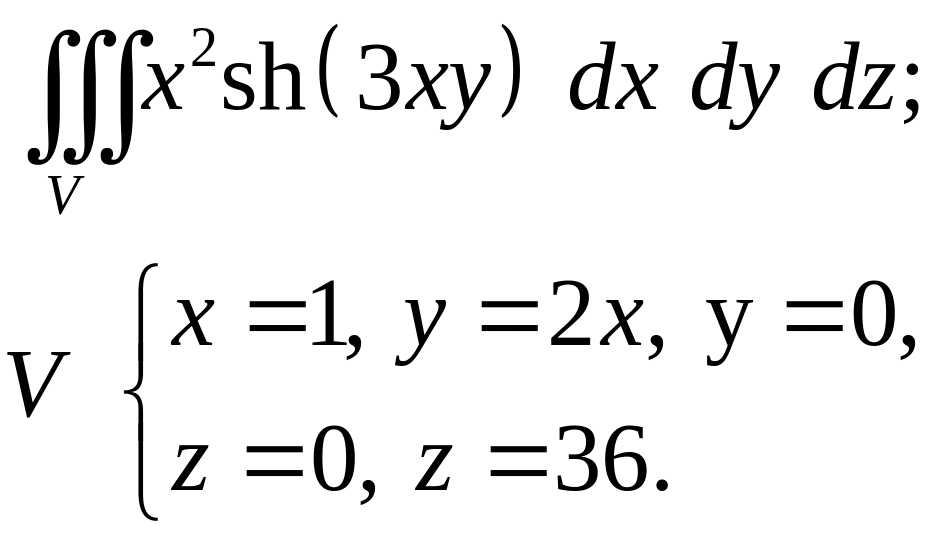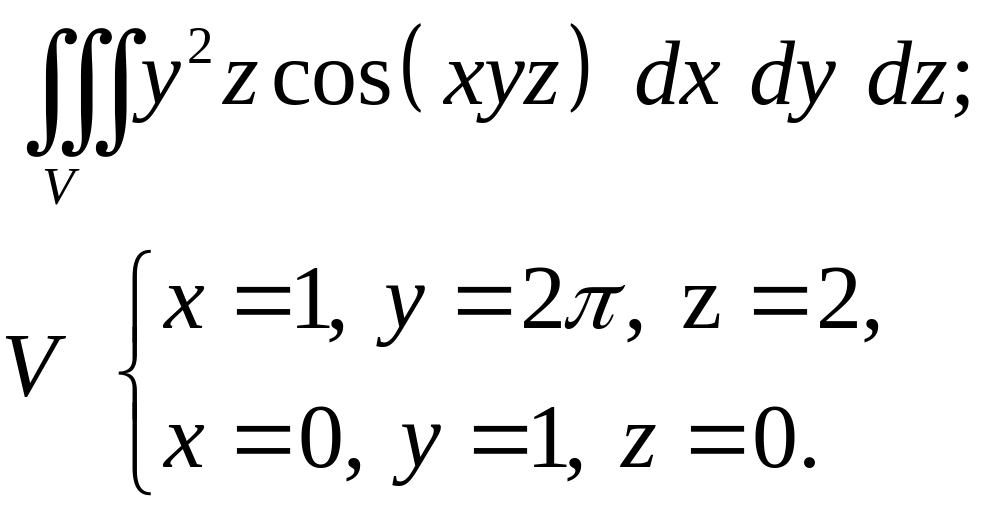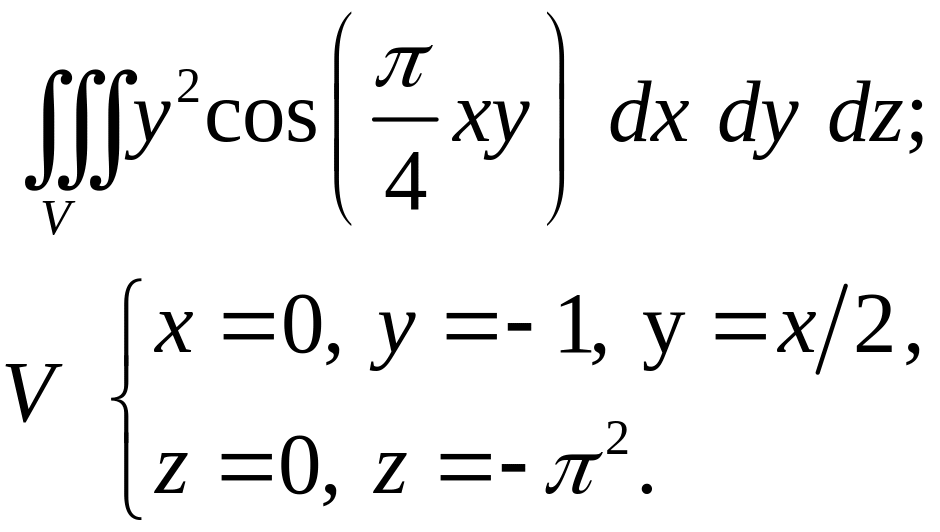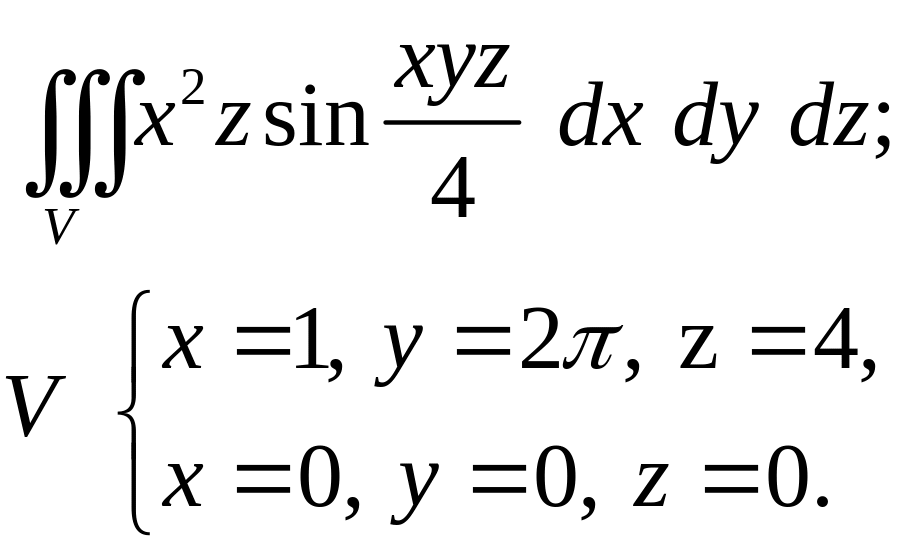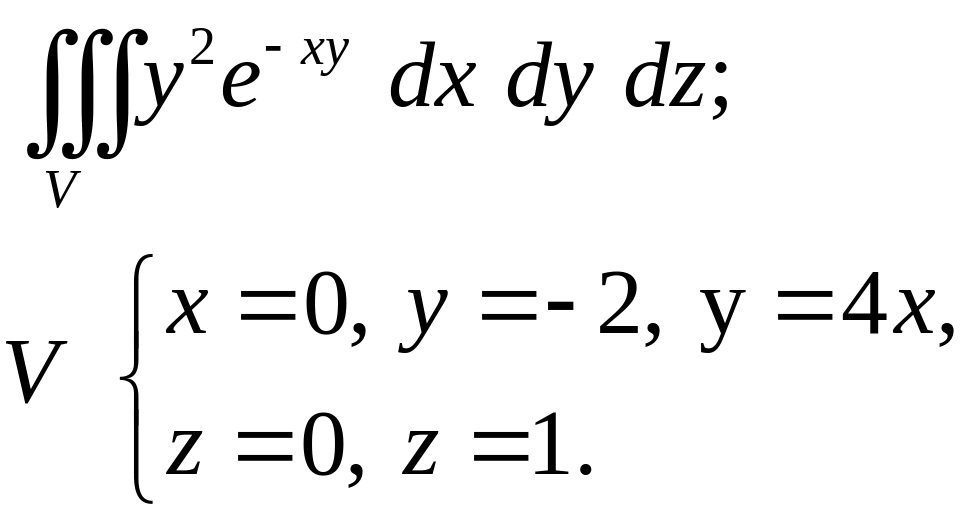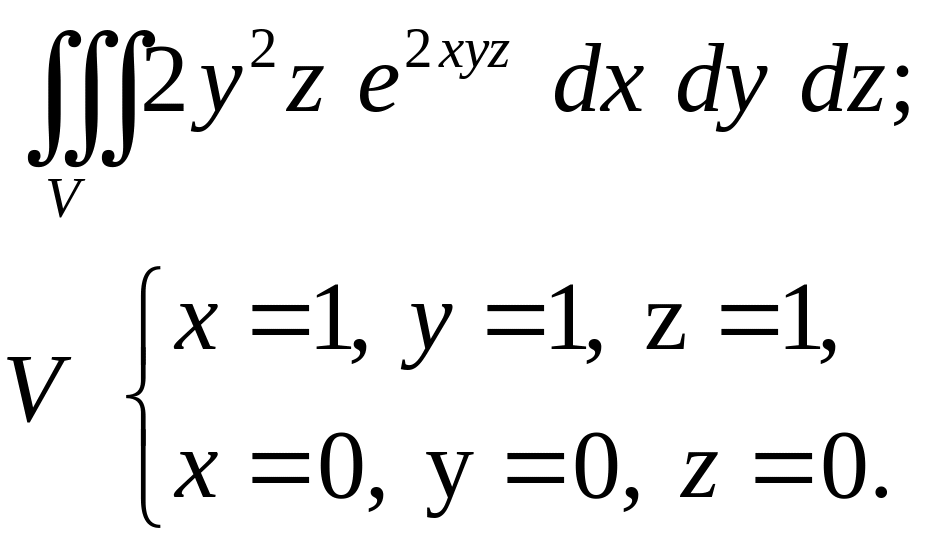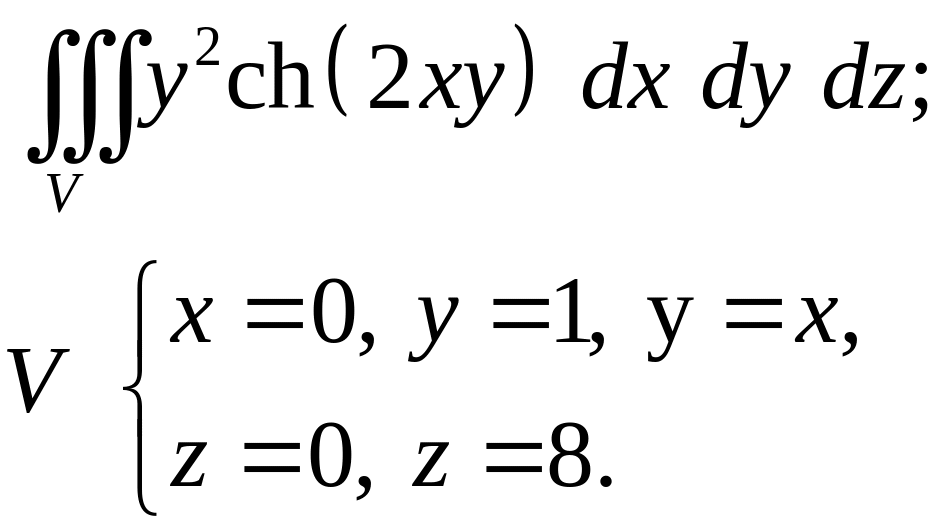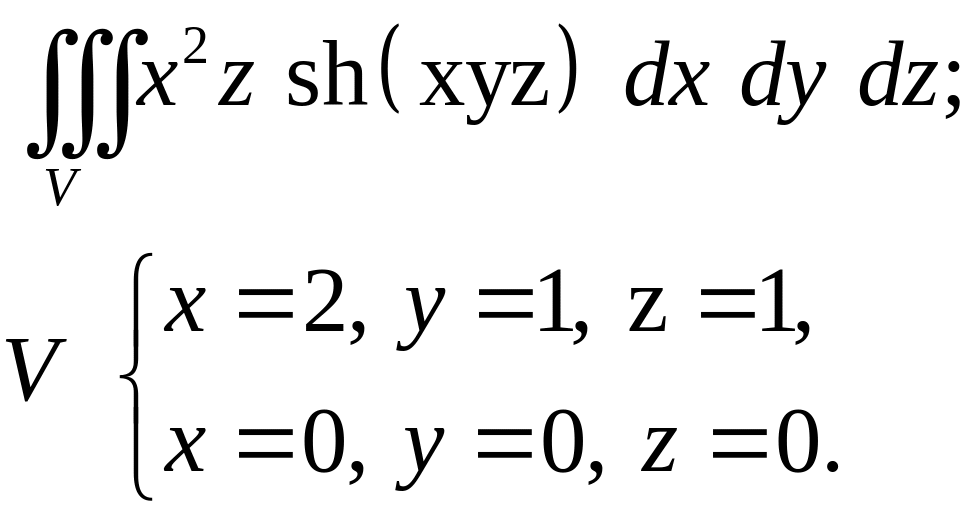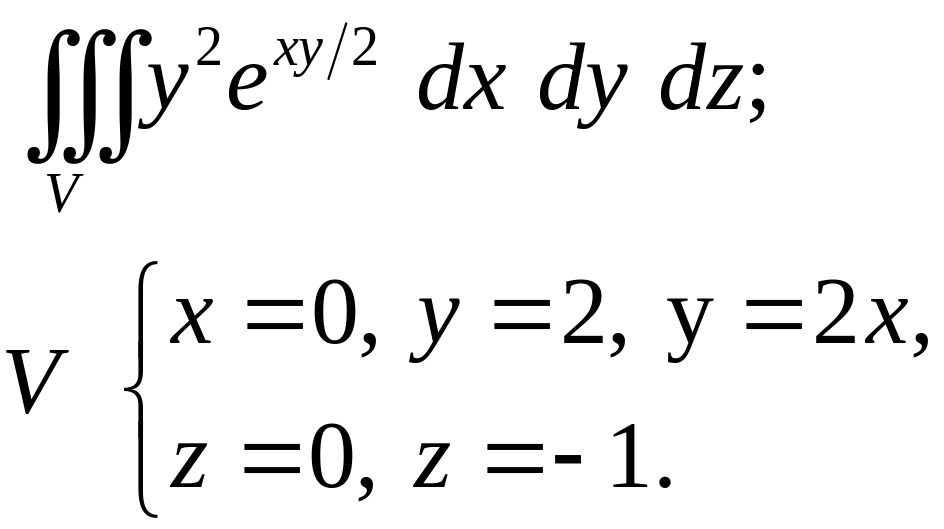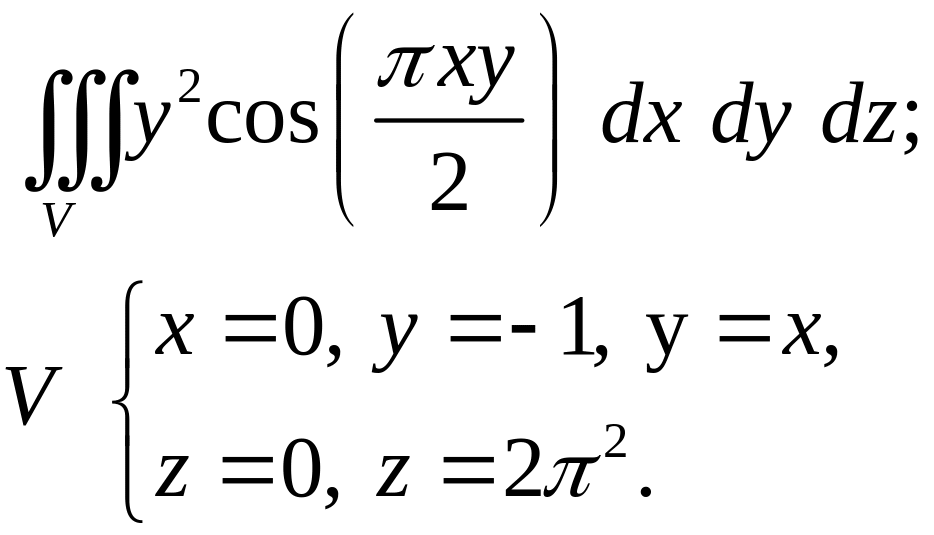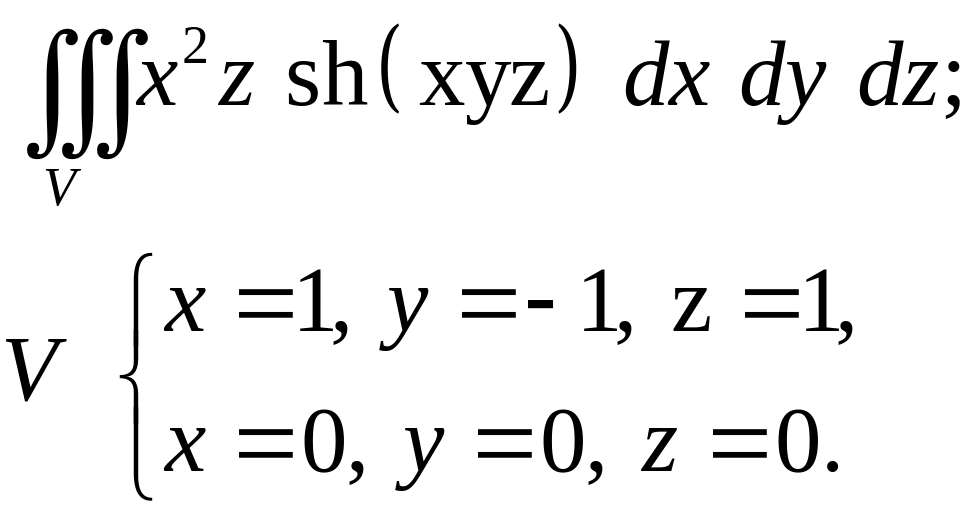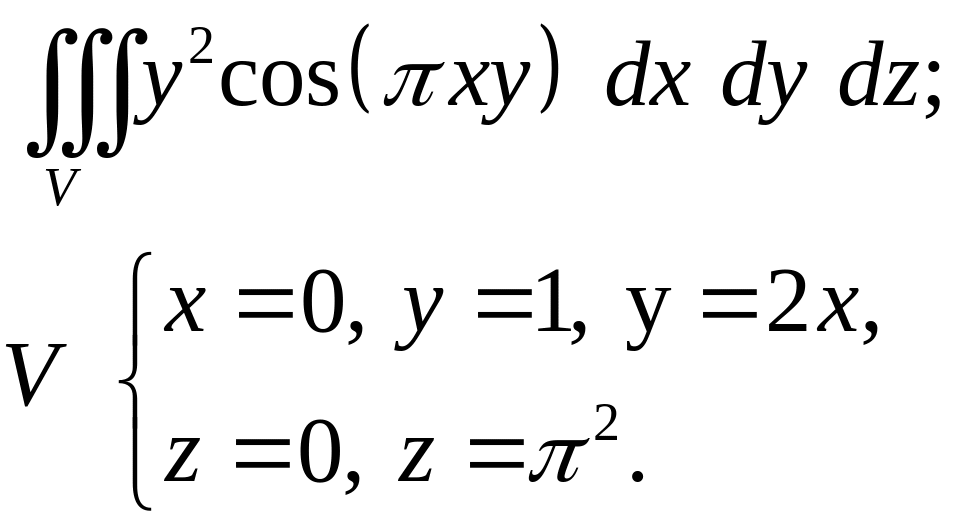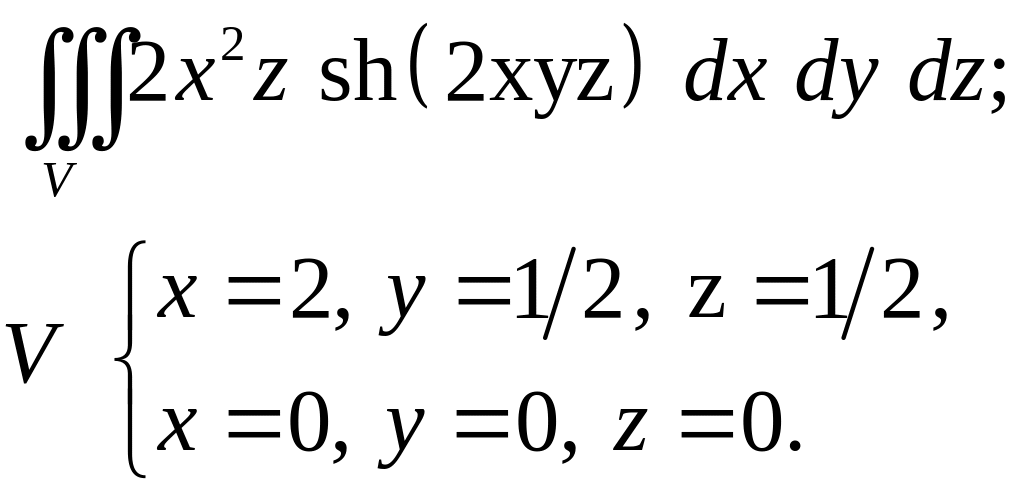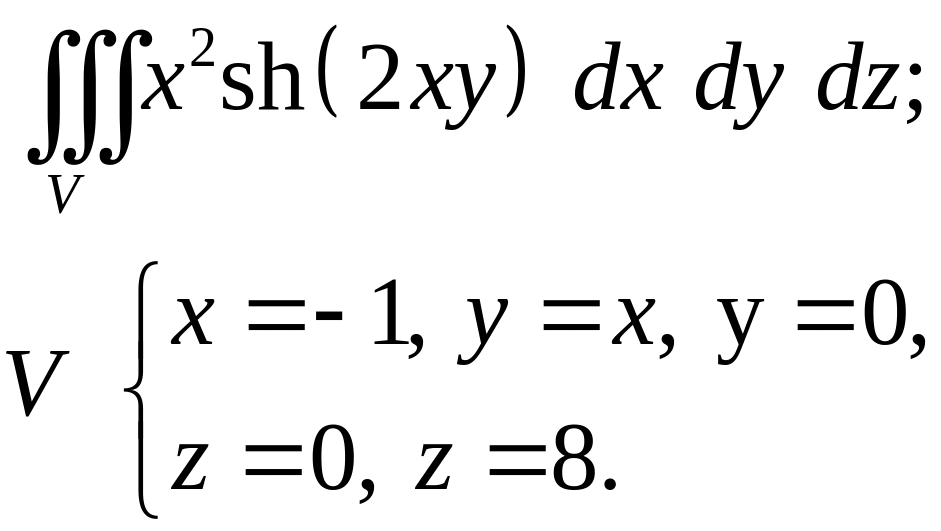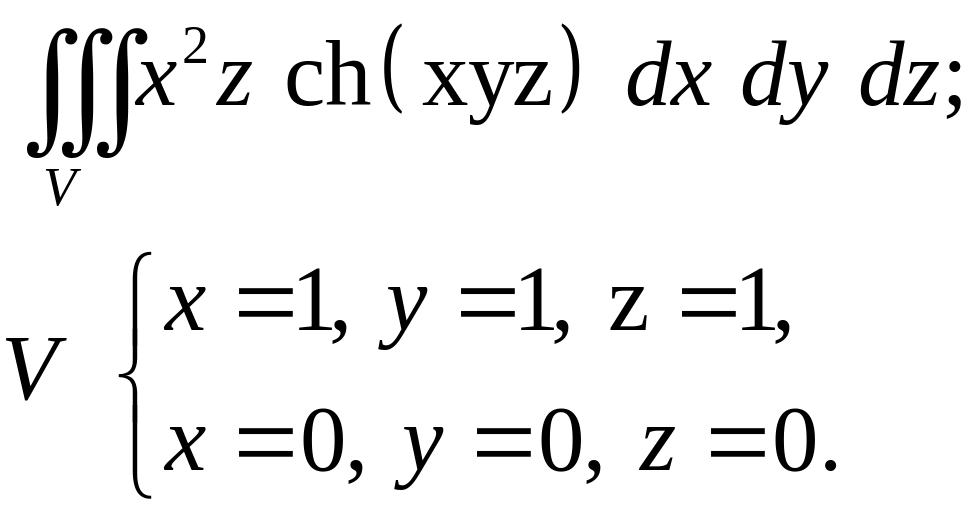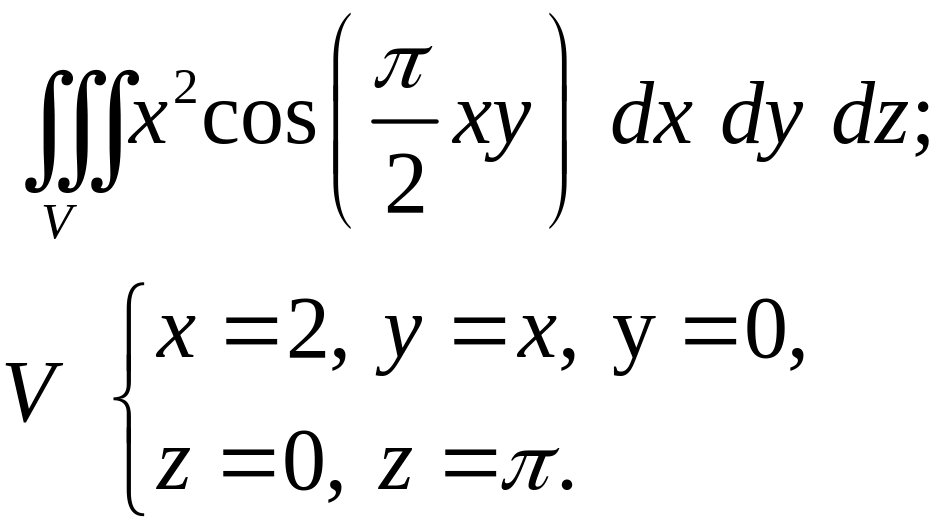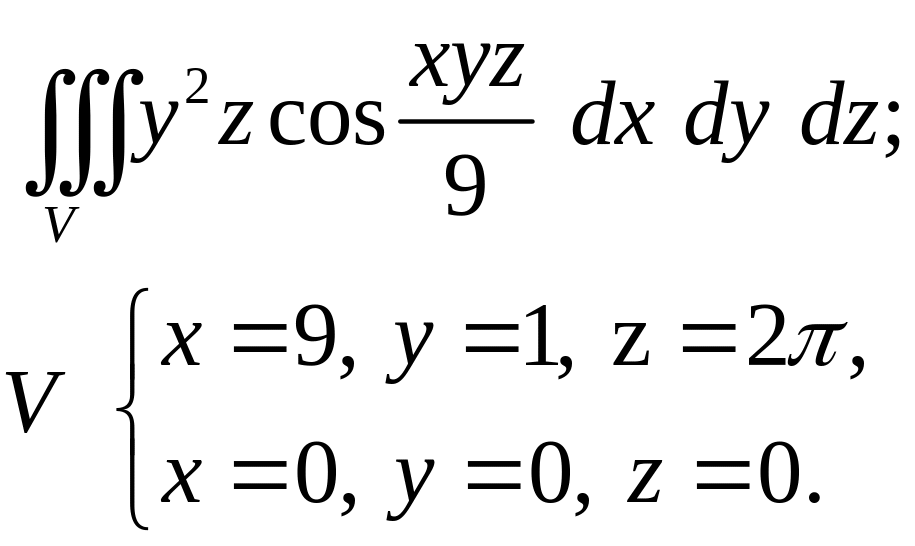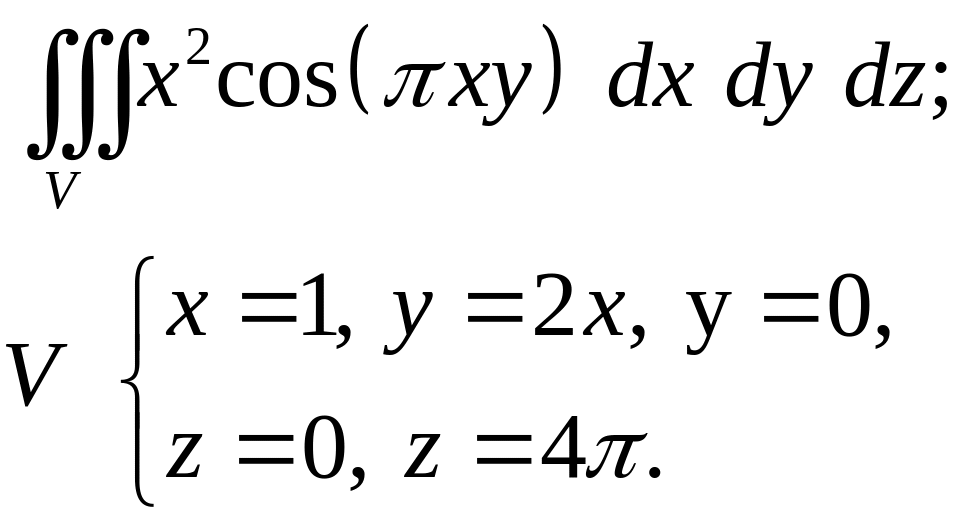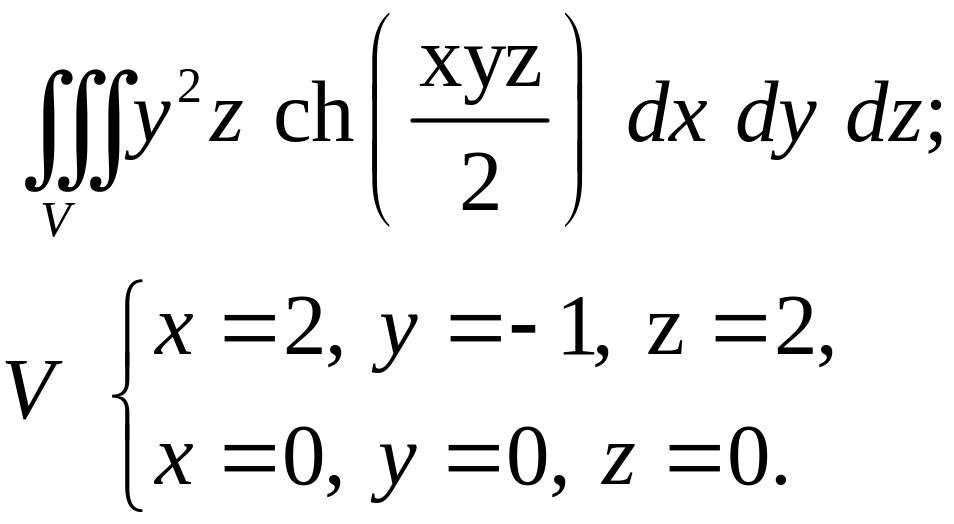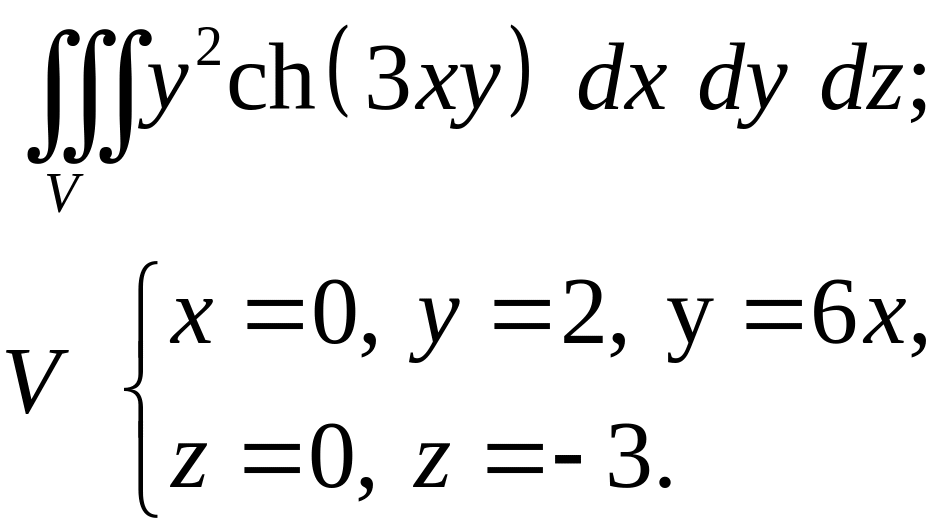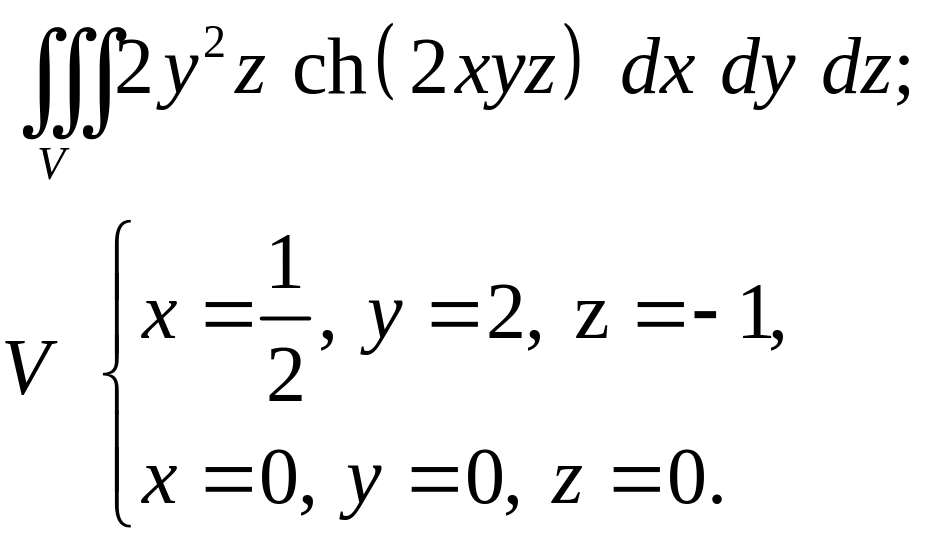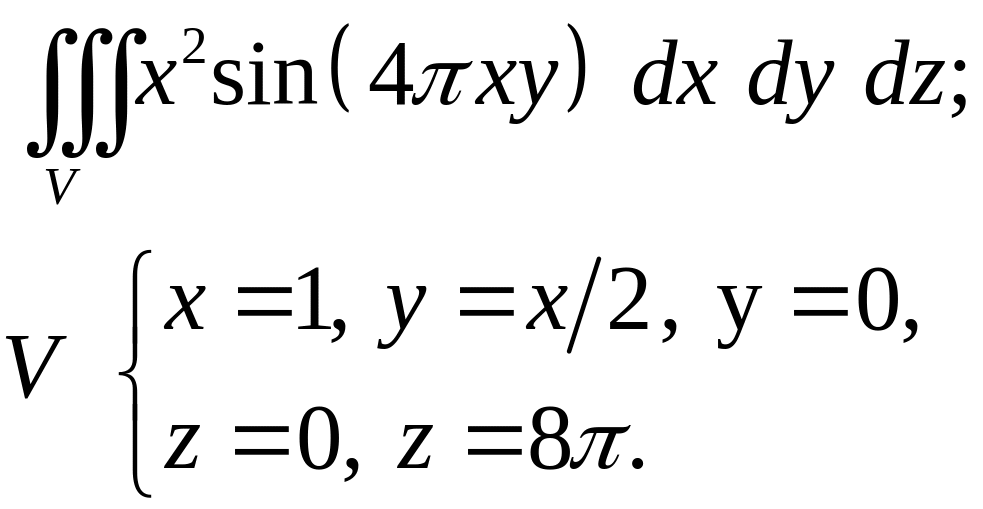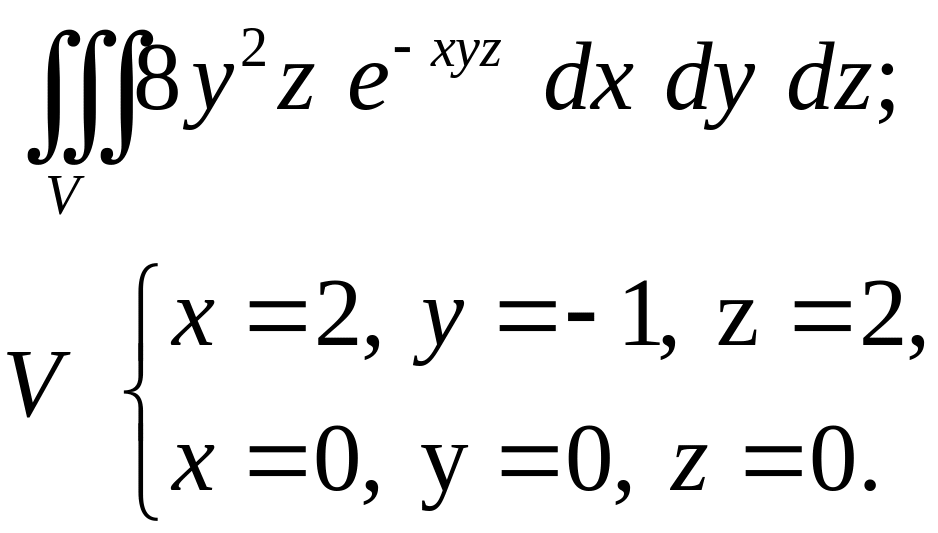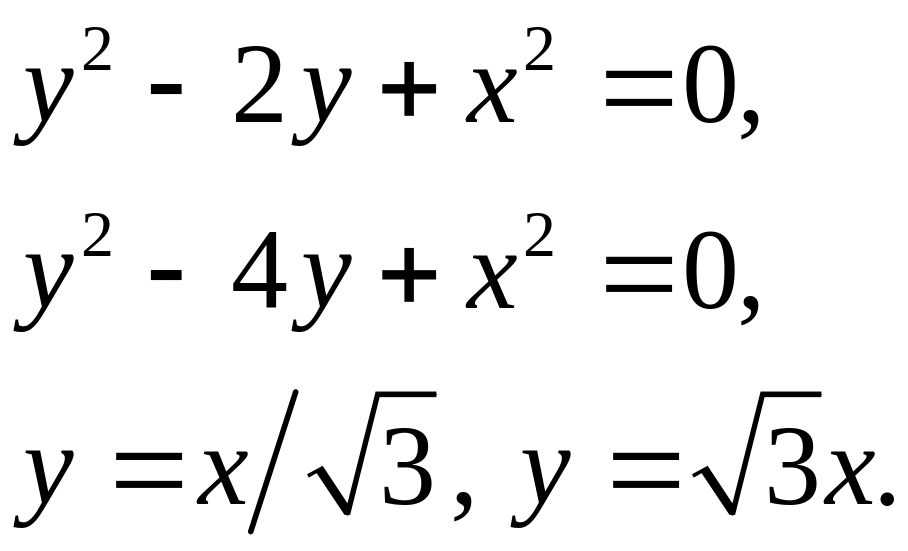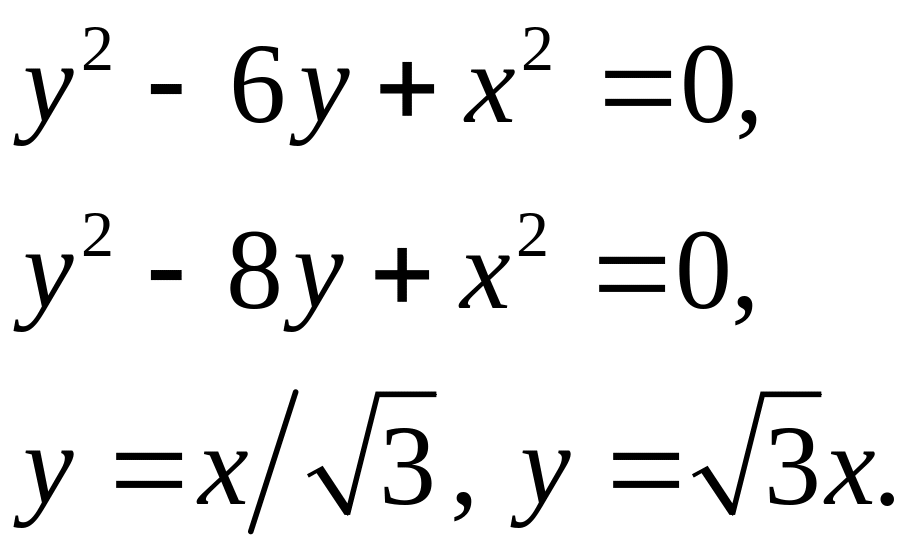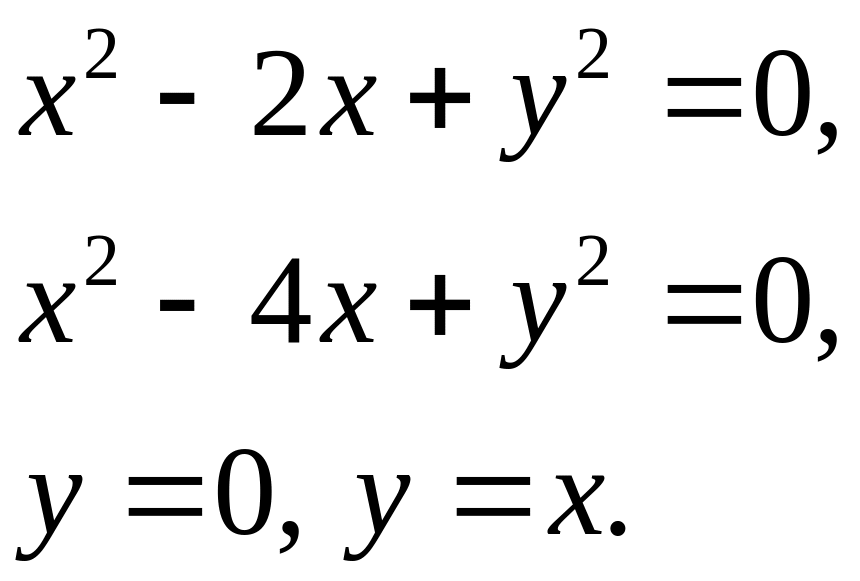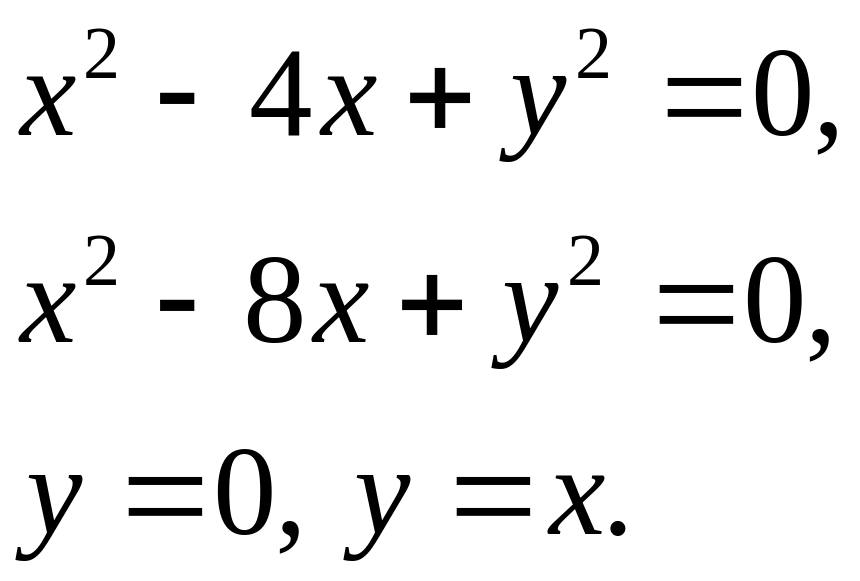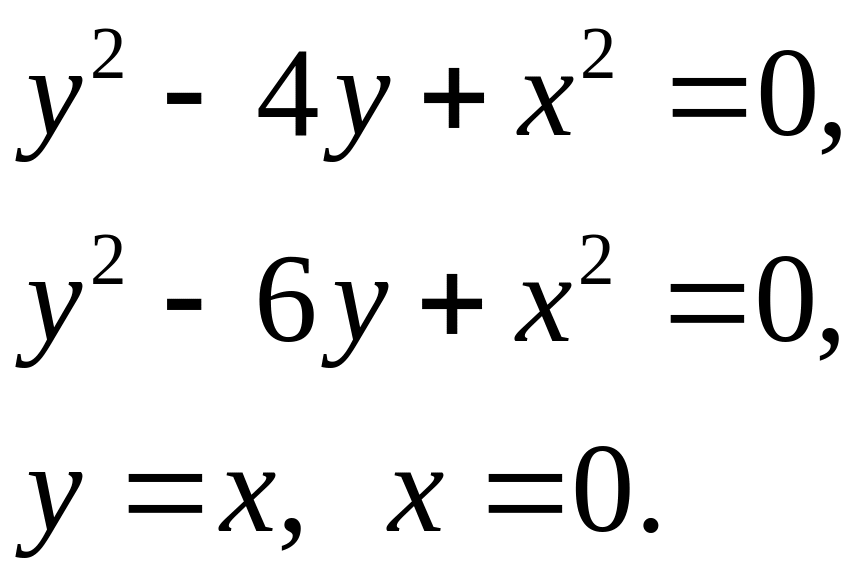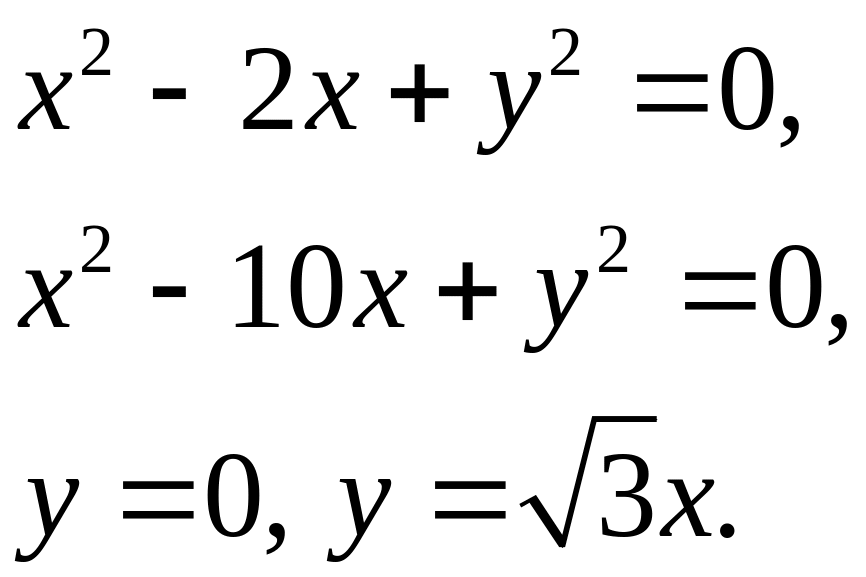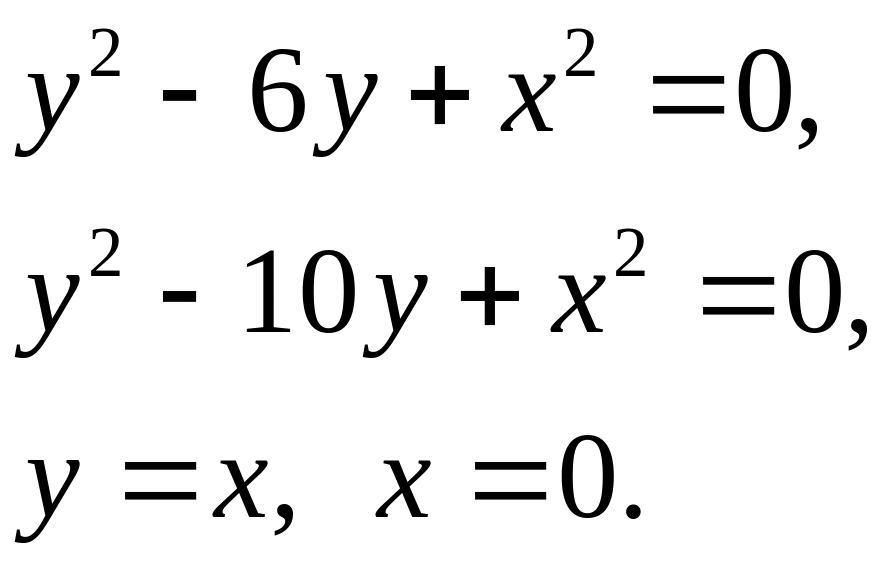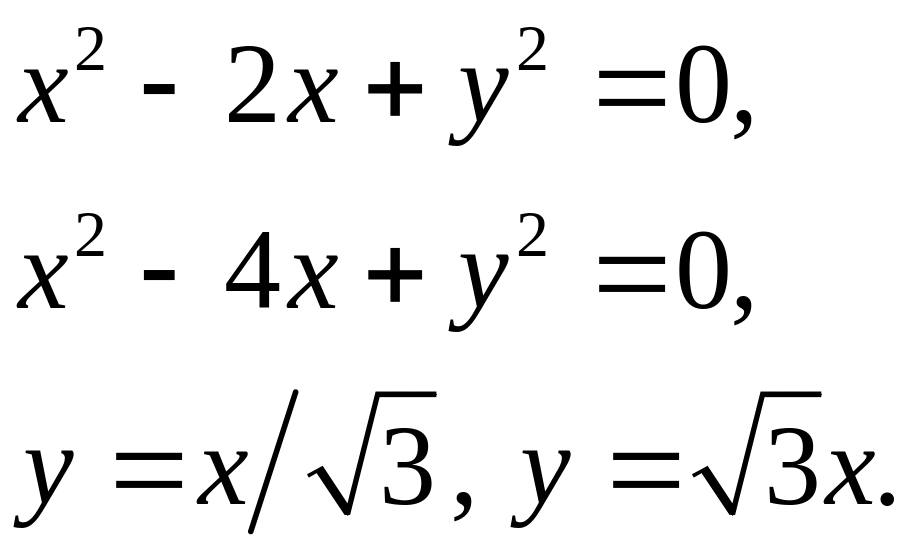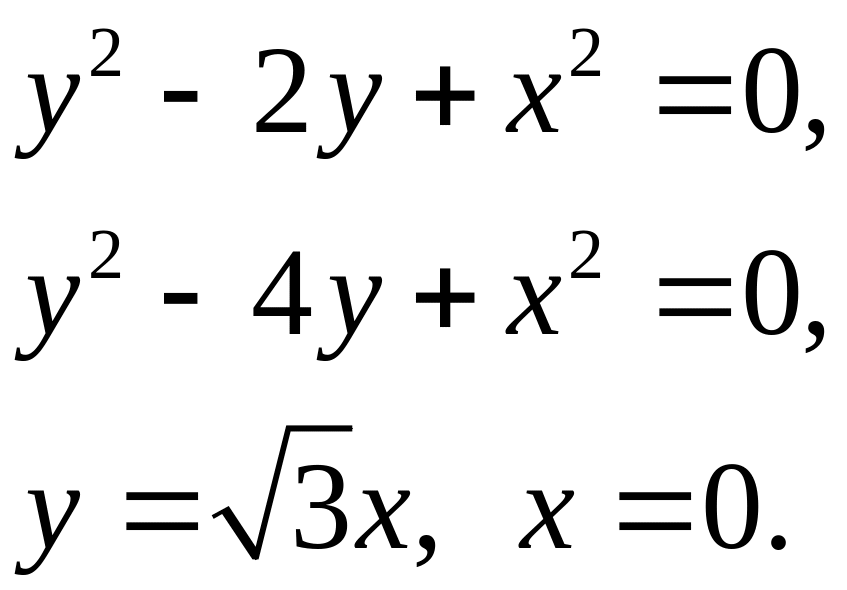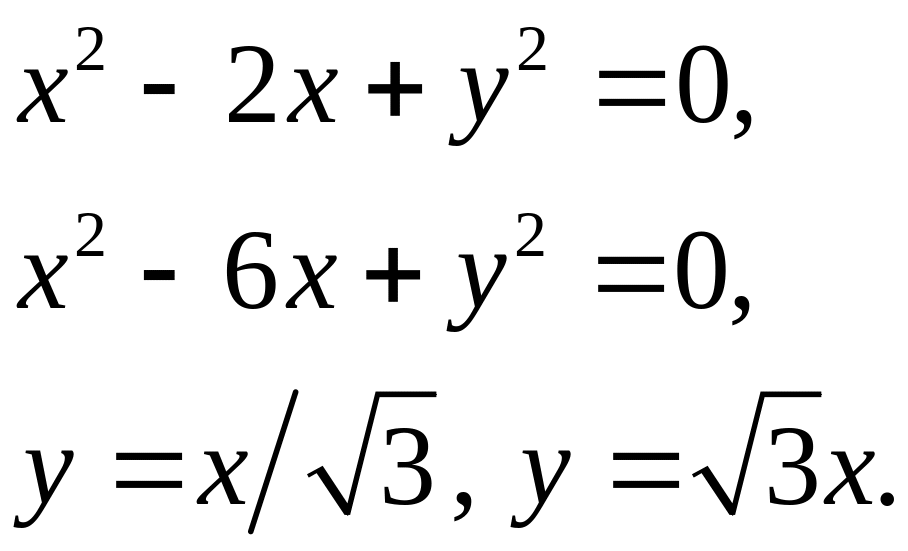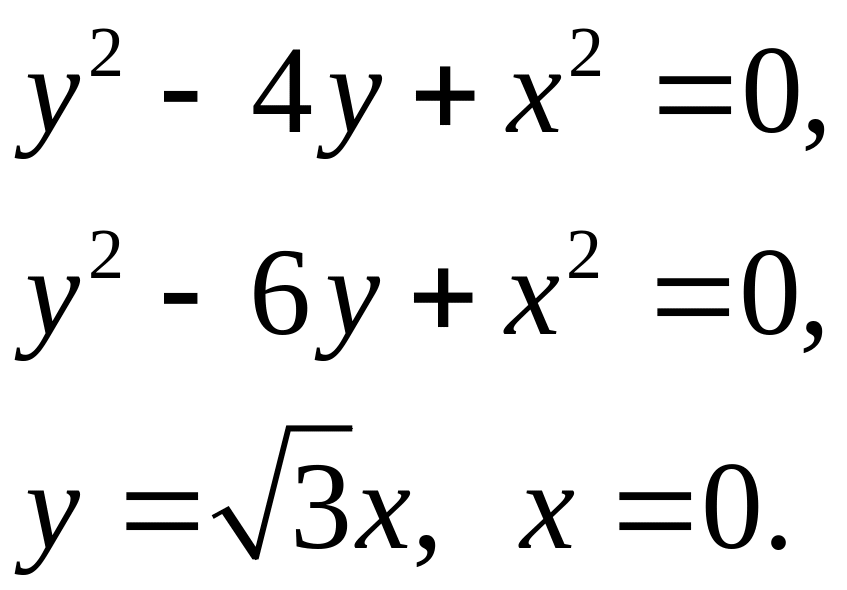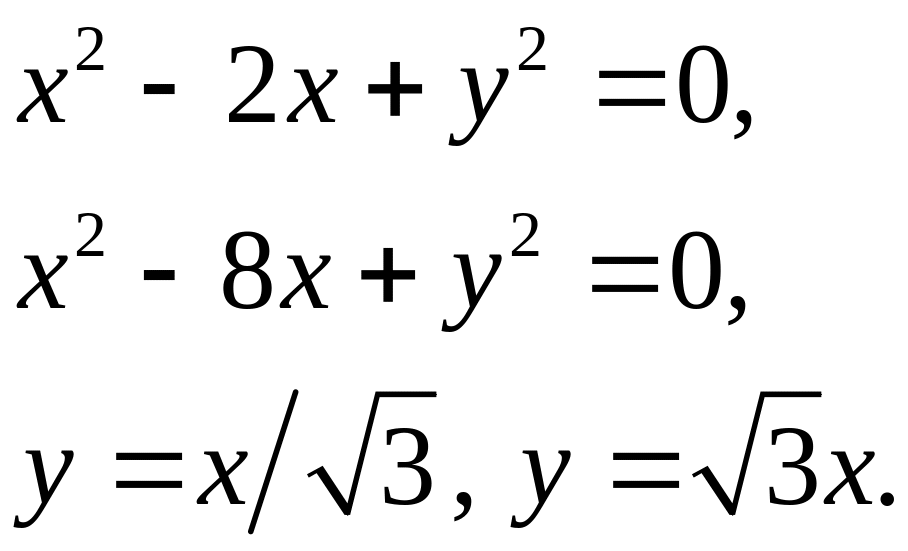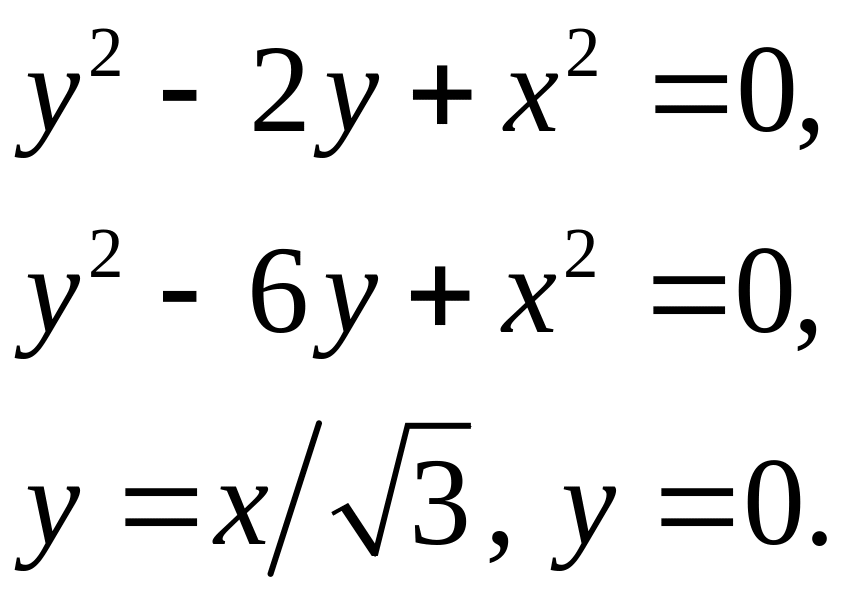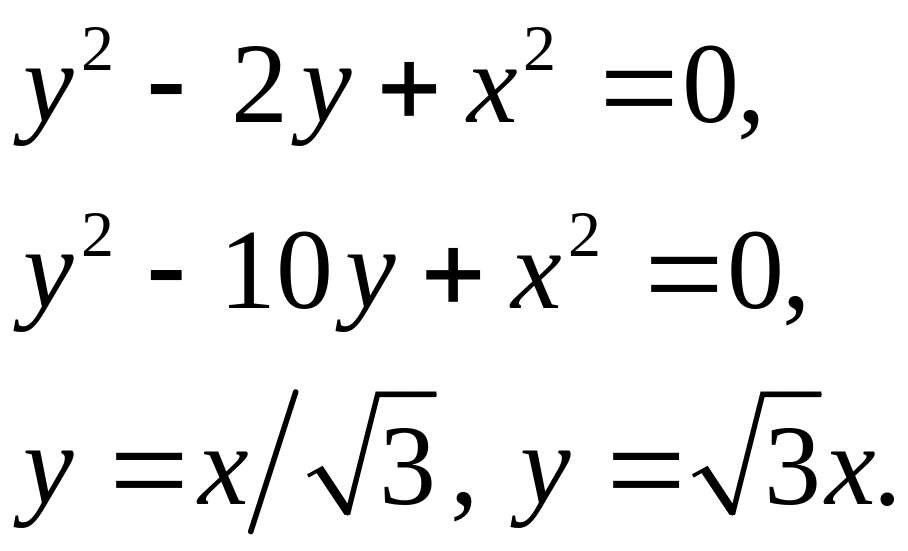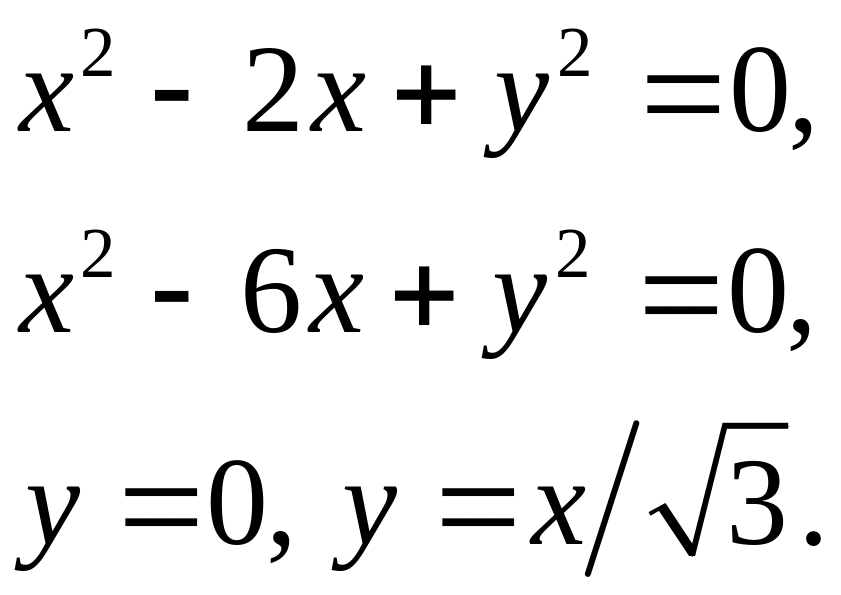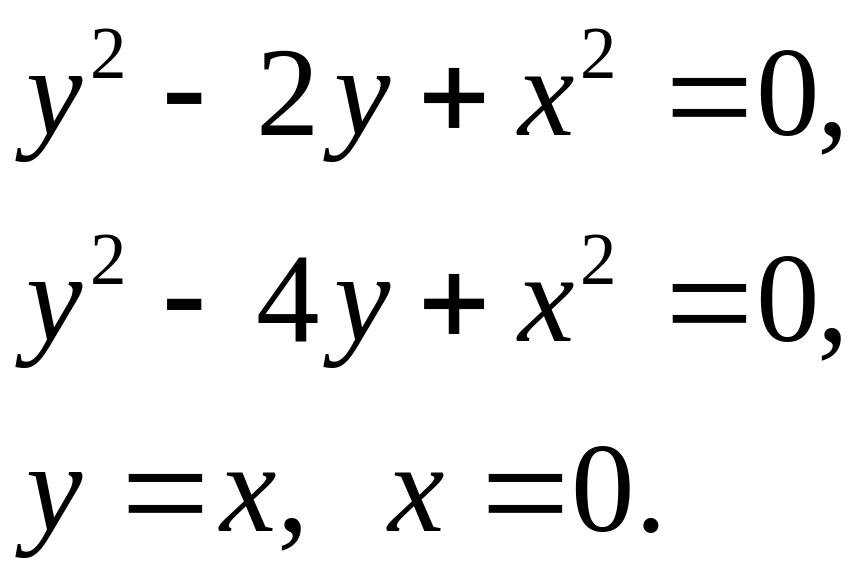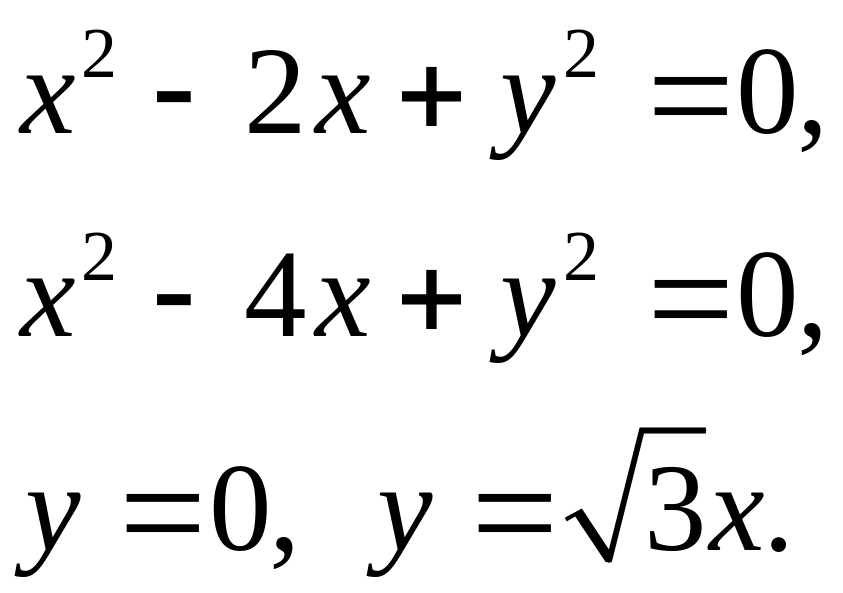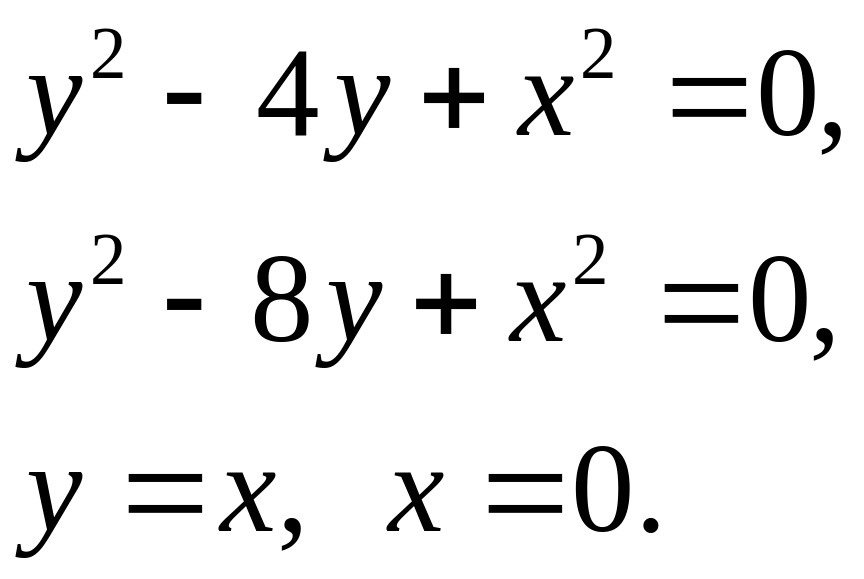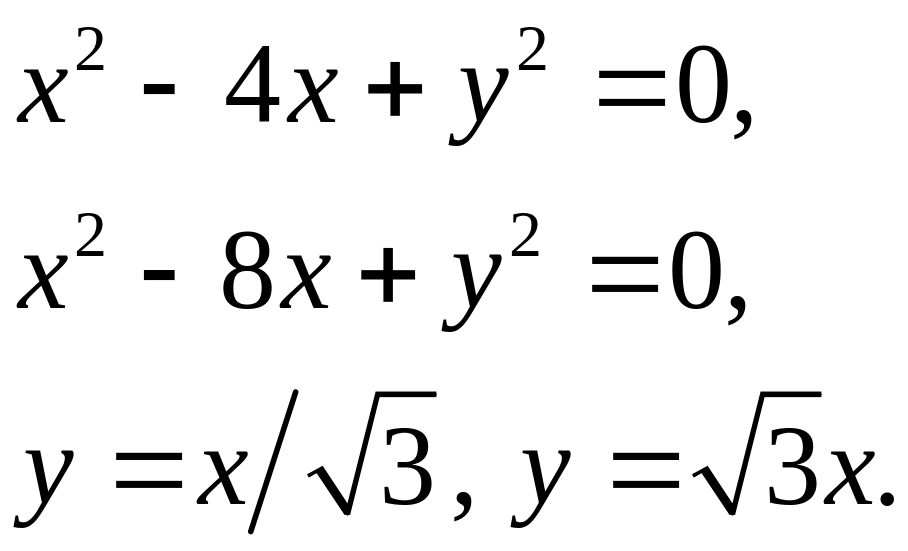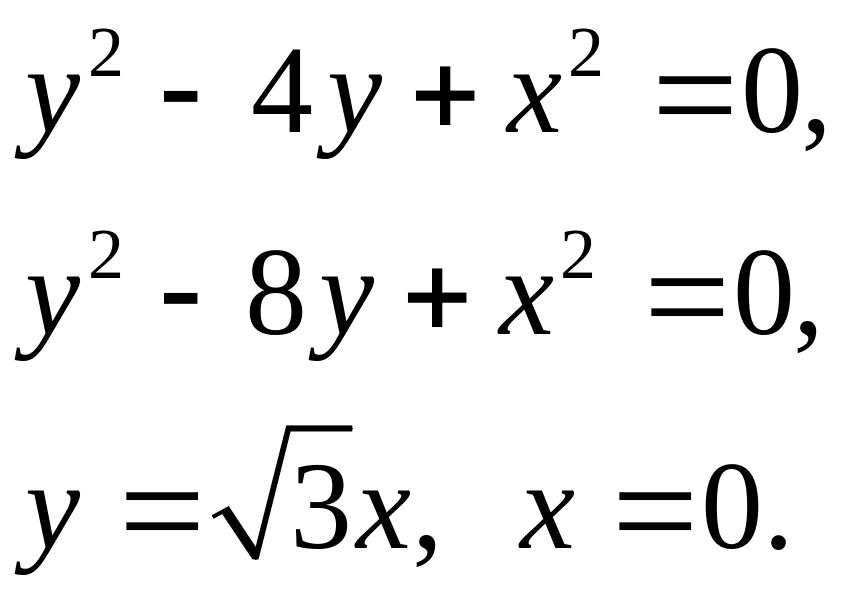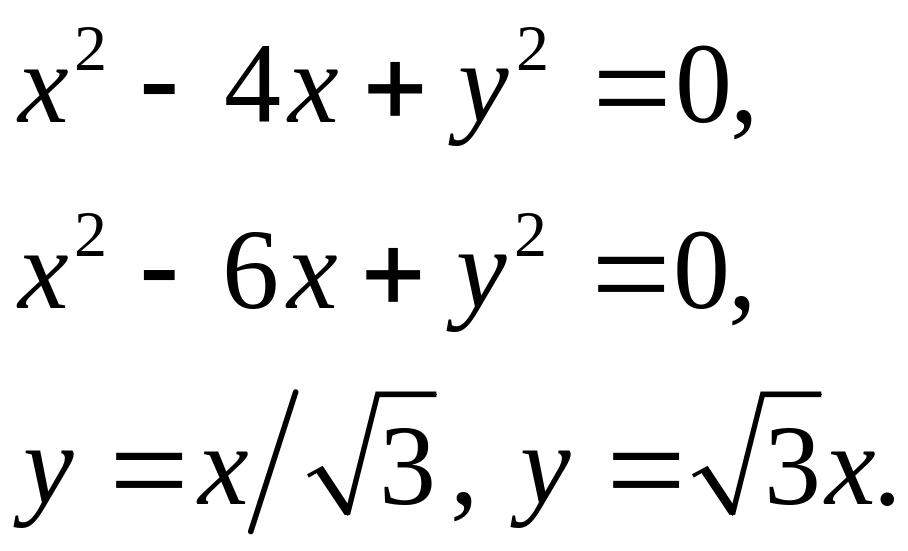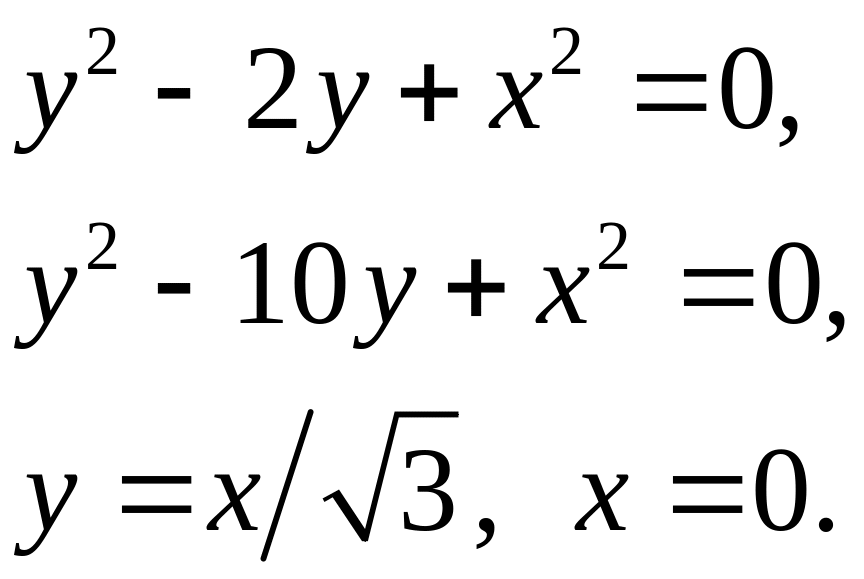ИДЗ 1. Кратные интегралы 5
Задача 1. Построить область интегрирования. Изменить порядок интегрирования. 5
Задача 2. Построить область интегрирования, вычислить двойной интеграл. 6
Задача 3. Построить область интегрирования. Вычислить интеграл. 7
Задача 4. Построить область интегрирования. Вычислить интеграл. 9
Задача 5. Найти площадь фигуры, ограниченной данными линиями (7). 11
Задача 6. Пластинка D задана неравенствами, - поверхностная плотность. Построить изображение пластины. Найти массу пластинки. (9) 13
Задача 7. Найти объем тела, заданного ограничивающими его поверхностями. (11) 14
Задача 8. Найти объем тела, заданного ограничивающими его поверхностями. (13) 16
Задача 9. Тело V задано ограничивающими его поверхностями, - плотность. Найти массу тела. (16) 17
ИДЗ 2. Скалярные и векторные поля. Криволинейные интегралы 20
Задача 1. 20
Задача 2. Найти векторные линии в векторном поле . Построить векторные линии в окрестности начала координат. 21
Задача 3. Вычислить данные криволинейные интегралы первого рода. Построить кривую L, указать направление интегрирования. 22
Задача 4. Вычислить данные криволинейные интегралы первого рода. Построить кривую L 23
Задача 5. Найти криволинейный интеграл второго рода векторного поля вдоль контура (в направлении, соответствующем возрастанию параметра ). Сделать чертеж контура. 24
Задача 6. Найти модуль циркуляции векторного поля вдоль контура . 26
Задача 7. С использованием криволинейных интегралов решить следующие задачи. Сделать иллюстрацию. 28
ИДЗ 3. Поверхностные интегралы и теория поля 30
Задача 1. Найти поверхностный интеграл первого рода по поверхности S, где S - часть плоскости (p), отсеченная координатными плоскостями (257 - 2) 30
Задача 2. Вычислить массу полусферы , если поверхностная плотность в каждой ее точке 30
Задача 3. Найти поверхностный интеграл второго рода от векторного поля через часть плоскости , расположенную в первом октанте (нормаль образует острый угол с осью ). Сделать чертеж плоскости и нормали 31
Задача 4. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя). Сделать чертеж поверхности 32
Задача 7. Найти наибольшую плотность циркуляции векторного поля в точке (273) 34
Задача 8. Проверить является ли векторное поле потенциальным и соленоидальным. В случае потенциальности поля найти его потенциал. 34
ИДЗ 4. Теория функций комплексного переменного и операционное исчисление 36
Задача 1. Восстановить аналитическую в окрестности точки функцию по известной действительной части или мнимой и значению 36
Задача 2. Для данной функции найти изолированные особые точки и определить их тип 36
Задача 3. Вычислить интеграл, построить область интегрирования и отметить особые точки подынтегральной функции. 37
Задача 4. Найти оригинал по заданному изображению 38
Задача 5. Решить дифференциальные уравнения с начальными условиями (задача Коши) операционным методом. 38
Образец титульного листа 41
Идз 1. Кратные интегралы Задача 1. Построить область интегрирования. Изменить порядок интегрирования.
1.1.
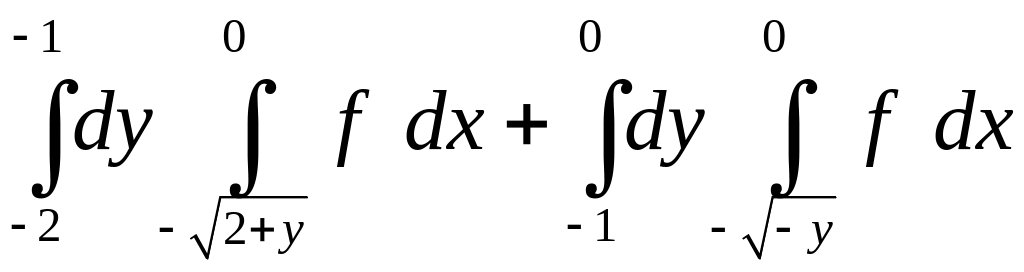. 1.2.
.
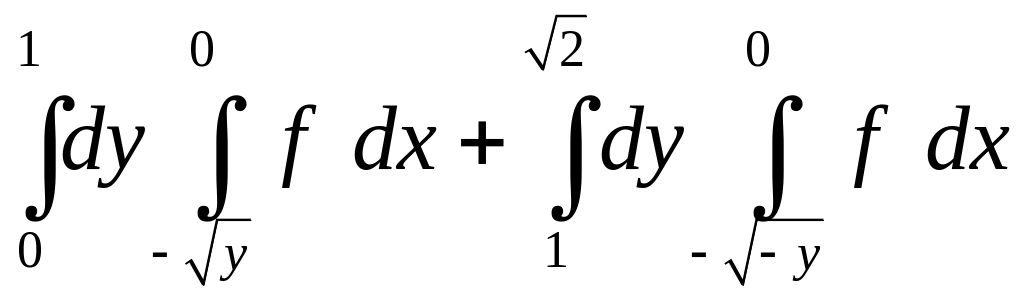1.3.
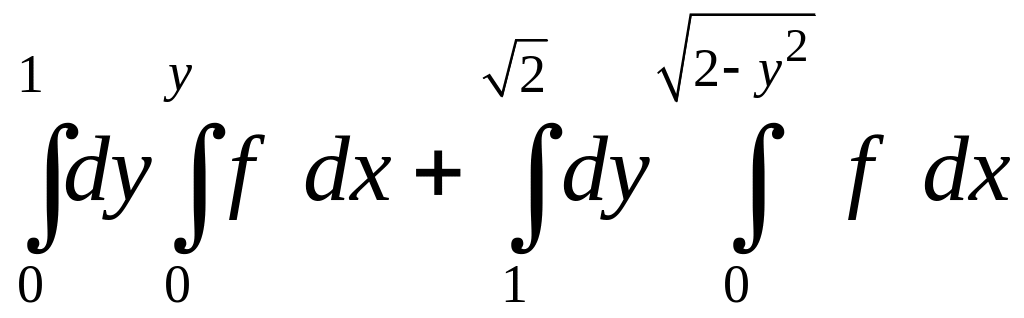. 1.4.
.
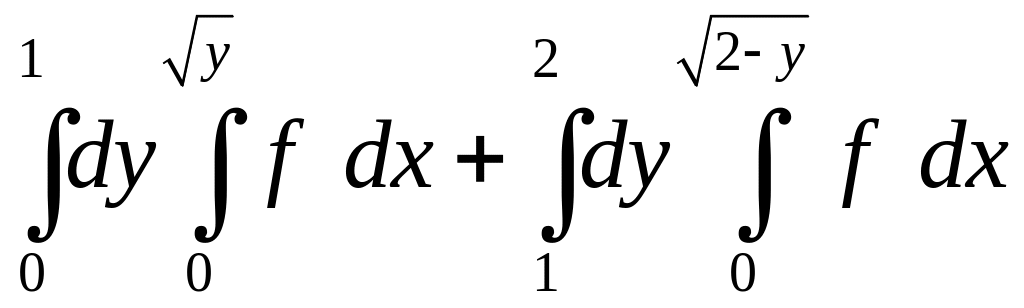1.5.
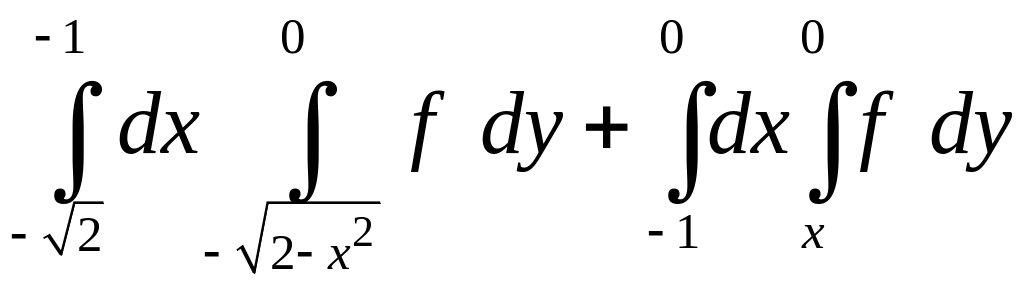. 1.6.
.
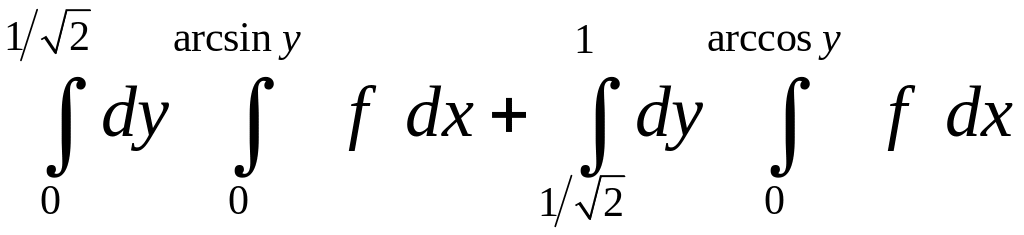1.7.
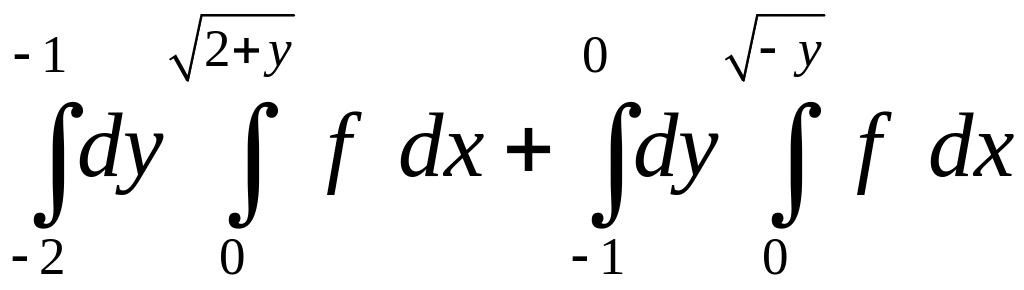. 1.8.
.
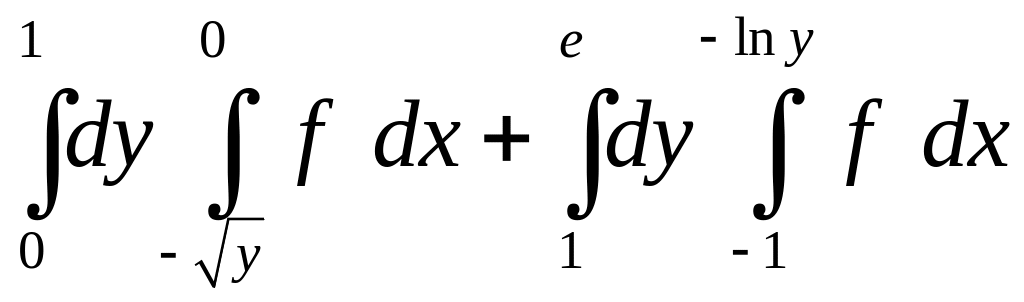1.9.
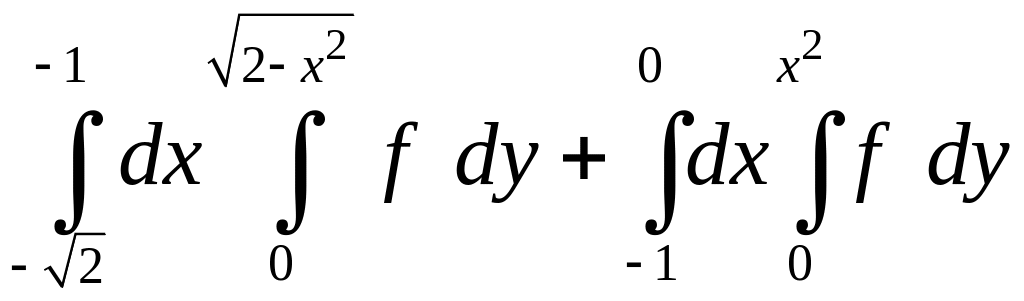. 1.10.
.
1.11.
. 1.12.
.
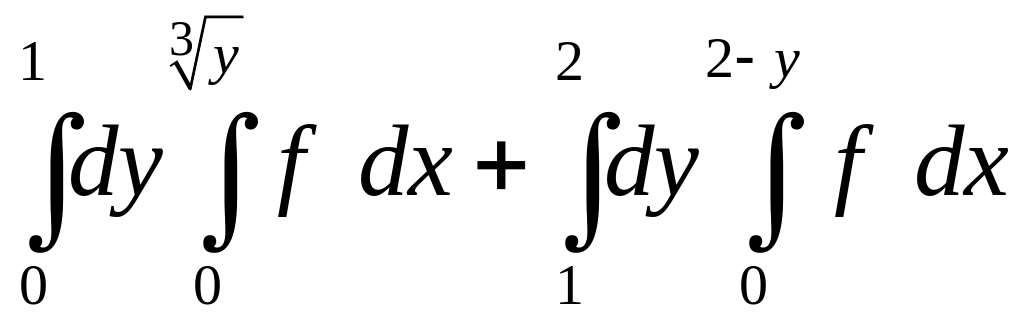1.13.
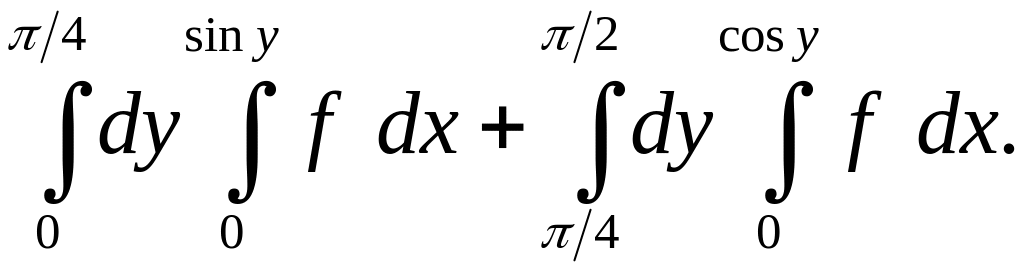. 1.14.
.
1.15.
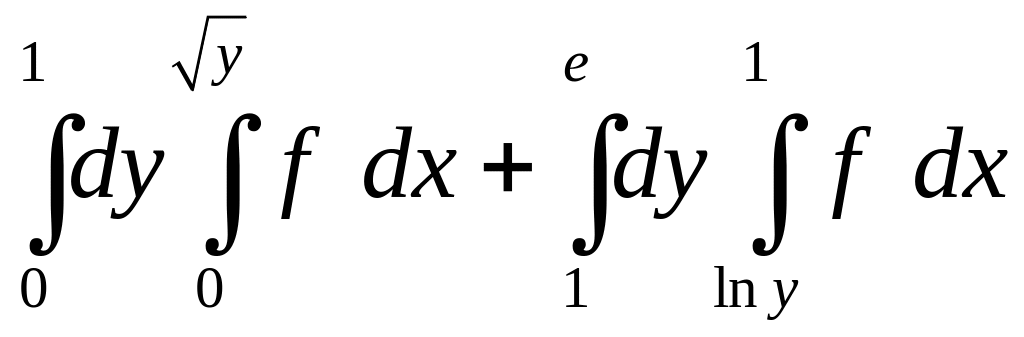. 1.16.
.
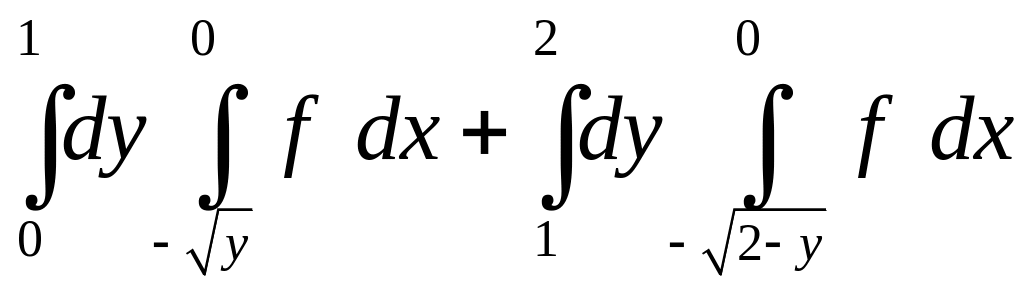1.17.
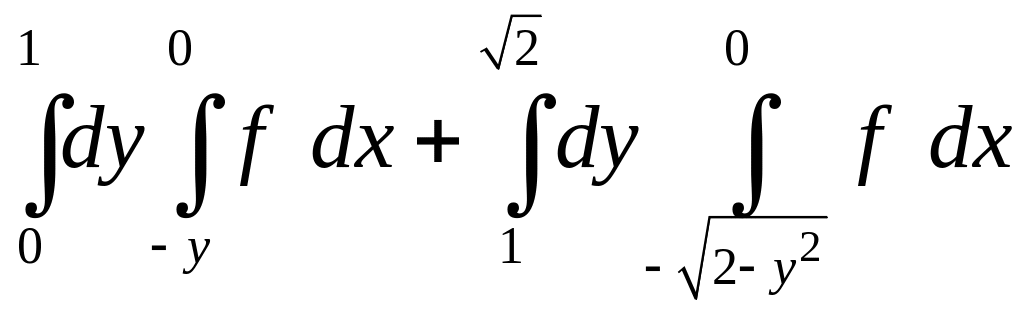. 1.18.
.
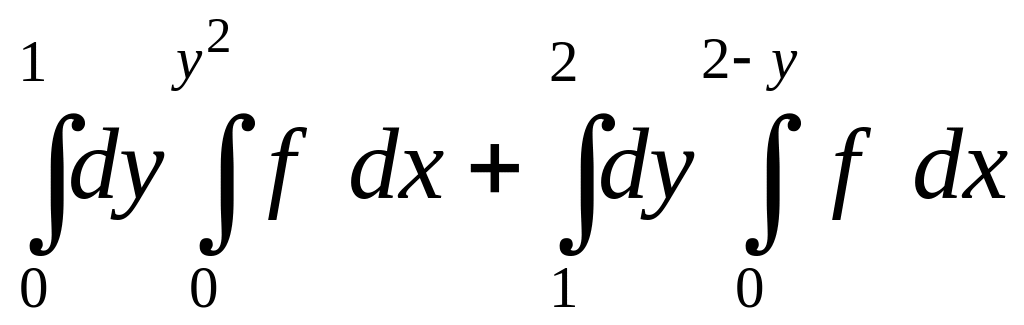1.19.
. 1.20.
.
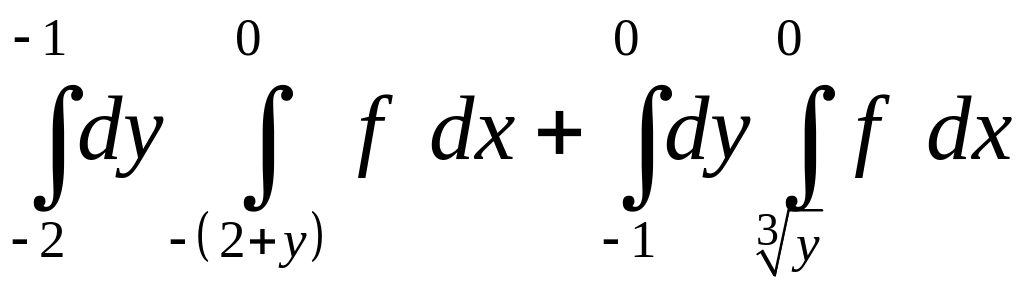1.21.
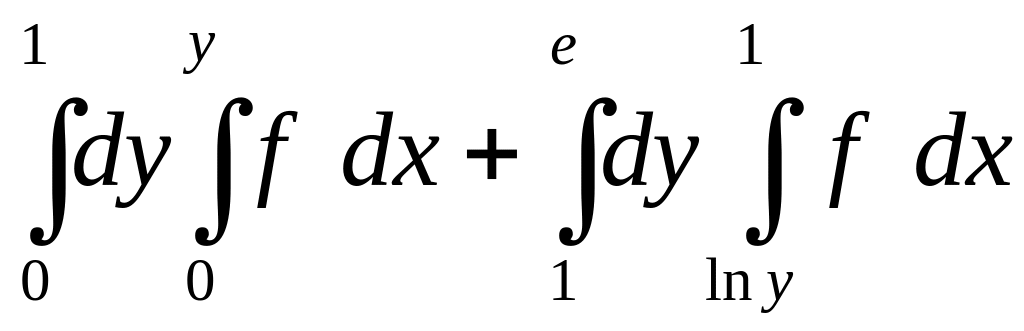. 1.22.
.
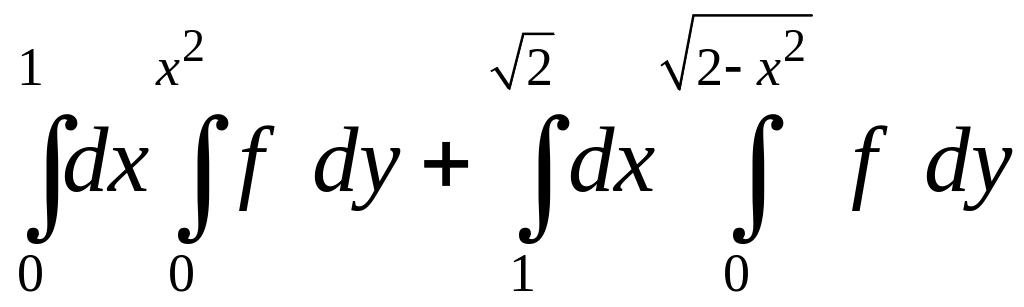1.23.
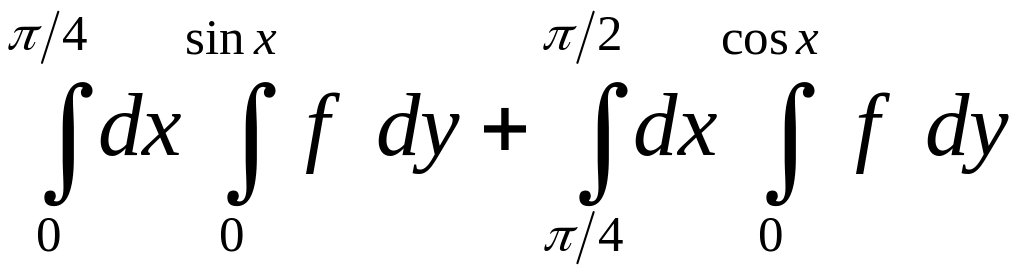. 1.24.
.
1.25.
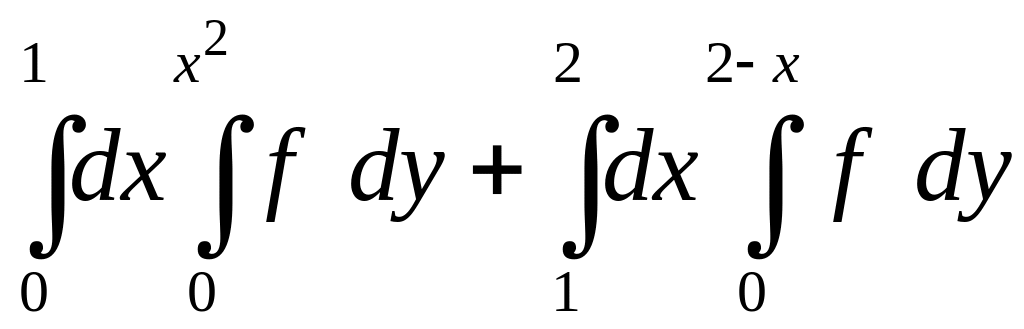. 1.26.
.
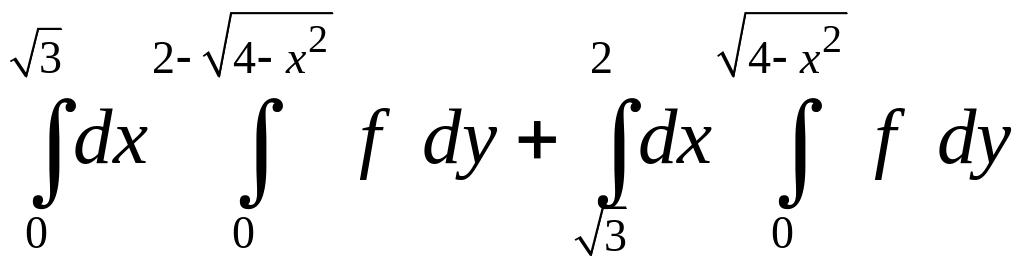1.27.
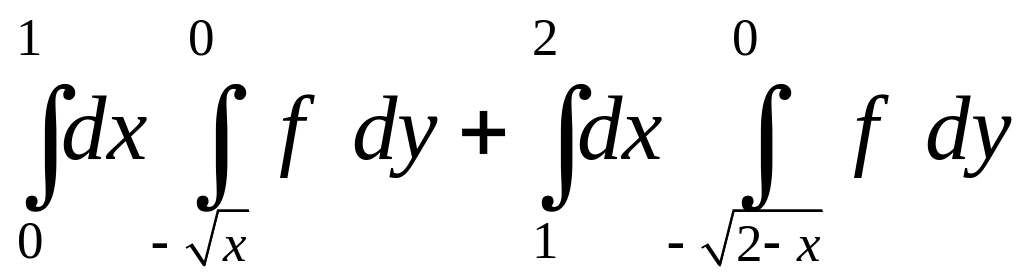. 1.28.
.
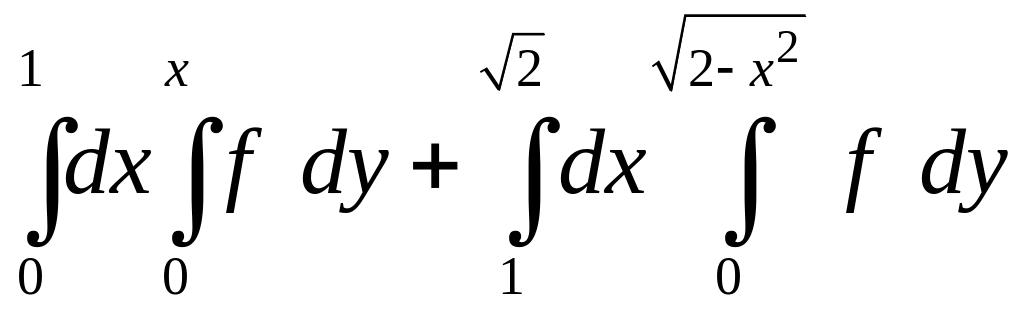1.29.
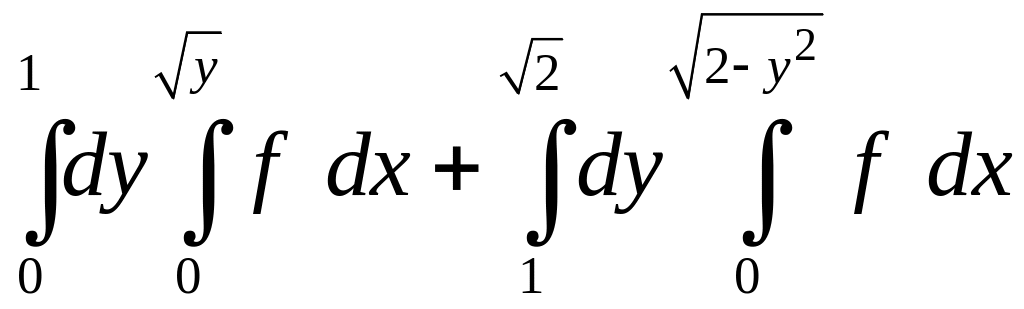. 1.30.
.
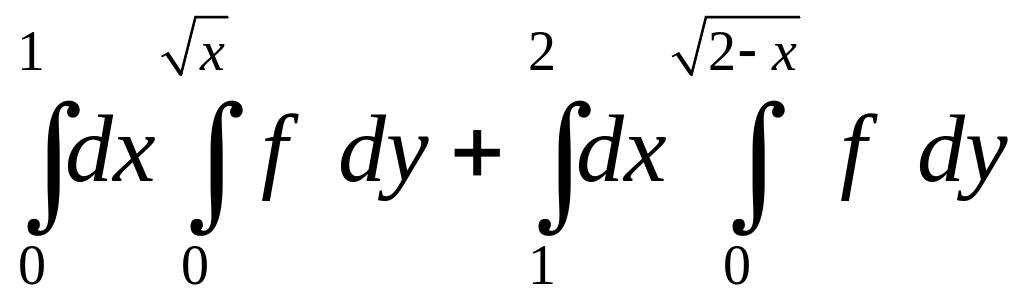1.31.
.
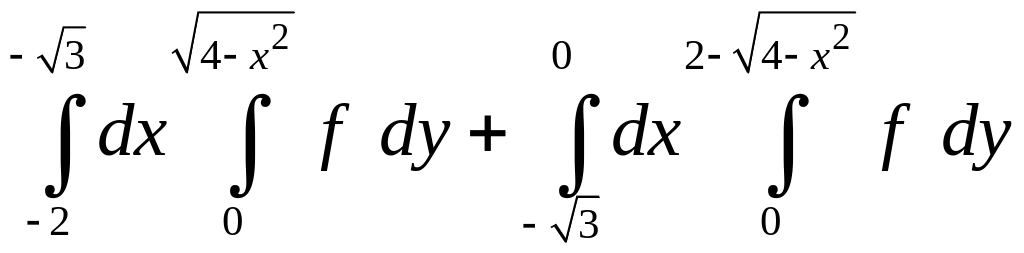Задача 2. Построить область интегрирования, вычислить двойной интеграл.
2.1.
|
2.2.
|
2.3.
|
2.4.
|
2.5.
|
2.6.
|
2.7.
|
2.8.
|
2.9.
|
2.10.
|
2.11.
|
2.12.
|
2.13.
|
2.14.
|
2.15.
|
2.16.
|
2.17.
|
2.18.
|
2.19.
|
2.20.
|
2.21.
|
2.22.
|
2.23.
|
2.24.
|
2.25.
|
2.26.
|
2.27.
|
2.28.
|
2.29.
|
2.30.
|
2.31.
Задача 3. Построить область интегрирования. Вычислить интеграл.
3.1.
|
3.2.
|
3.3.
|
3.4.
|
3.5.
|
3.6.
|
3.7.
|
3.8.
|
3.9.
|
3.10.
|
3.11.
|
3.12.
|
3.13.
|
3.14.
|
3.15.
|
3.16.
|
3.17.
|
3.18.
|
3.19.
|
3.20.
|
3.21.
|
3.22.
|
3.23.
|
3.24.
|
3.25.
|
3.26.
|
3.27.
|
3.28.
|
3.29.
|
3.30.
|
3.31.
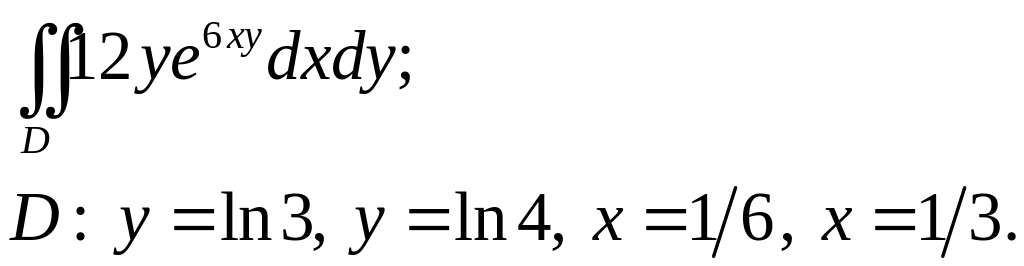
Задача 4. Построить область интегрирования. Вычислить интеграл.
4.1.
|
4.2.
|
4.3.
|
4.4.
|
4.5.
|
4.6.
|
4.7.
|
4.8.
|
4.9.
|
4.10.
|
4.11.
|
4.12.
|
4.13.
|
4.14.
|
4.15.
|
4.16.
|
4.17.
|
4.18.
|
4.19.
|
4.20.
|
4.21.
|
4.22.
|
4.23.
|
4.24.
|
4.25.
|
4.26.
|
4.27.
|
4.28.
|
4.29.
|
4.30.
|
4.31.
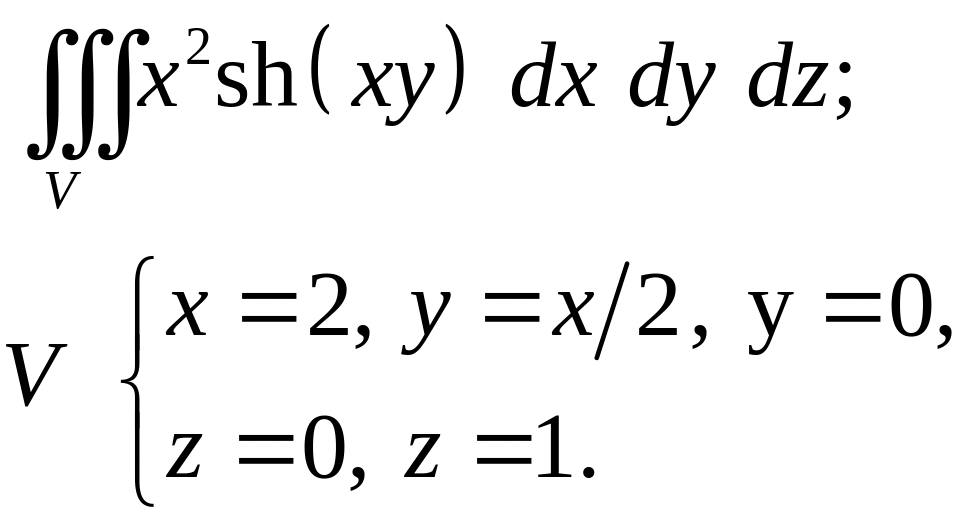
Задача 5. Найти площадь фигуры, ограниченной данными линиями (7).
5.1.
|
5.2.
|
5.3.
|
5.4.
|
5.5.
|
5.6.
|
5.7.
|
5.8.
|
5.9.
|
5.10.
|
5.11.
|
5.12.
|
5.13.
|
5.14.
|
5.15.
|
5.16.
|
5.17.
|
5.18.
|
5.19.
|
5.20.
|
5.21.
|
5.22.
|
5.23.
|
5.24.
|
5.25.
|
5.26.
|
5.27.
|
5.28.
|
5.29.
|
5.30.
|
5.31.
