2.2 Преобразование графиков

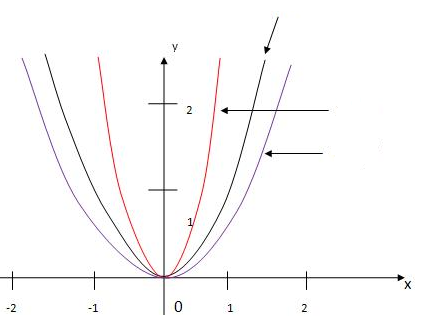
Задание 2.2.1 На графике указать графики функций ; ; .

Задание 2.2.2 Построить график функции с помощью элементарных преобразований.

Задание 2.2.3 По графику определить вид элементарного преобразования и формулу функции.

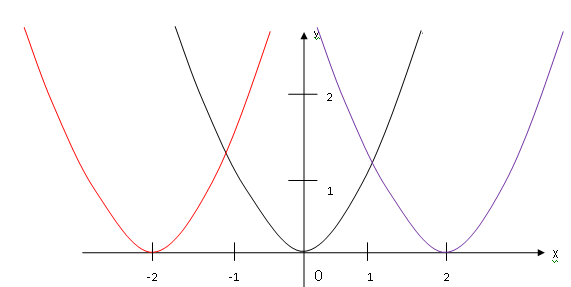
Решение:____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Задание 2.2.4 Пошагово описать принцип построения графика функции

1)________________________________________________________

2)________________________________________________________

3)________________________________________________________

_{Задание} 2.2.5 В одной системе координат построить графики функций _{, , .}

2.3 Четные и нечетные функции

Задание 2.3.1 Дать определения.

Функция называется ______, если для любого из области определения выполняется равенство

Функция называется нечетной, если для любого из области определения выполняется равенство __________.

Задание 2.3.2 Указать четную функцию.

а) ;

б) ;

в) ;

г) ;

д) .

Задание 2.3.3 Определить свойство четности или нечетности функции

а) функция четная;

б) функция нечетная;

в) свойствами четности и нечетности не обладает.

Задание 2.3.4 По графику функции определить четность или нечетность функции.

1 ) ____________________________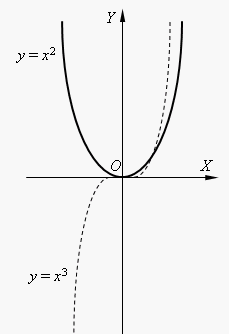

2) ____________________________

Задание 2.3.5 Дописать утверждение.

График четной функции симметричен относительно ____. График четной функции симметричен относительно ________.

Задание 2.3.6 Проверить на четность или нечетность функции и .

1)___________________________________________________________________________________________________________________________________________2)___________________________________________________________________________________________________________________________________________

Задание 2.3.7 Привести примеры четной и нечетной функции.

Четные функции________________________________________________________

Нечетные функции______________________________________________________

2.4 Возрастание и убывание функции

Задание 2.4.1 Дописать определения.

Функция _________ на множестве , если большему значению аргумента соответствует большее значение функции.

Функция __________ на множестве , если большему значению аргумента соответствует меньшее значение функции.

Задание 2.4.2 Определить промежуток возрастания функции .

а)[1;+∞);

б) ;

в) ;

г) ;

д)

Задание 2.4.3 Значение функции в точке равно ____________.

Задание 2.4.4 Дописать определение.

Функция называют непрерывной на промежутке , если _______________________________________________________________.

Задание 2.4.5 Найти промежутки возрастания и убывания функции .

Решение:_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Ответ:________________________________________________________

Задание 2.4.6 По графику функции определите промежутки возрастания и убывания.

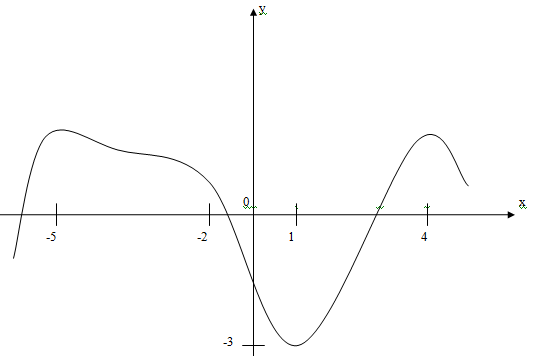
Решение:

Функция возрастает на промежутке_________________________________

Функция убывает на промежутке ___________________________________

Задание 2.4.7 Найти значение функции в точках -2; 4; 0; -3.

Решение.

_________________________________________________________

_________________________________________________________

_________________________________________________________

_________________________________________________________

Ответ:___________________________________________________________