19. Основные законы распределения.

Трапециидальное распределение – к ним относятся равномерное(рис 1,а), собственное трапец-е(1б) и треугольное(Симпсона –рис 1в). Мат ожидание всех трапец-х распределений: Хс=(Х1+Х2)/2.

Равномерное распределение имеет погрешности квантования цифровых приборов, погреш-ть механ стрелки-указателя. Суммируясь м-у собой эти погрешности образуют трапециидальное распределение с различным соотношением сторон.

Нормальное распределение(Гаусса)

Р(Х)=(1/(σ *2π))*е в степени –(Х-Хд)2/2σ2

σ – параметр распределения рассеивания, равных СКО.

Хд – центр распределения, = мат ожиданию.

t=Х-Хд, F(t)=1/2п*∫е в ст. -0,5t2 по dt (-оо;t)

Р(t)=1/2п*е в ст. -0,5t2

Определенный интеграл с переменным верхним пределом называется ф-ей Лапласа:Ф(t)=1/2п*∫е в ст. -0,5t2 по dt (0;t); F(t)=0,5 + Ф(t)

Уплощенное распределение – композиция равномерного и к-либо экспон-го распределения-рис.

Семейство кривых распределения Стьюдента.

Эти законы описывают плотность распред-я среднеарифметического, вычисленного по N случайных отчетов нормального распределения совокупности. При статист обработке результатов многократных измерений их вид зависит от числа отчета и N по кот находится среднеарифметическое значение, поэтому и говорят о семействе распределения.

Особенности расп-я Стьюдента:

1 при N<3 их СКО=оо, т.е. дисперсионная оценка ширины разброса не работает;

2 класс-ий аппарат моментов для оценки формы и ширины этого распределения с малым числом степеней свободы не работает, и их ширина и форма могут быть определены лишь с пом доверит-ой и энтропийной оценок.

Двухмодальное распределение.

1 Дискретное двухзначное распределение – расп-е при кот с равной вероятностью встречеется только 2-а значения случайной величины(рис).

2 Арксинусоидальное распределение(рис).

3 Остро и кругло вершинное двухмод распределение – композиция дискретного двухзначного и экспоненциального распределений с различными значениями коэф А альфа-рис.

Р(Х)=[А/(2п*σ*Г(1/2))]*е в ст. /(Х-Хд)/2σ/А

А>2 – островершинное р-е, А<2 – кругловершинное распр-е.

20. Точечные оценки законов распределения.

При использовании дискретных случ величин возникают задачи нахождения точечных оценок пар-ов функции распределения на основе выборки, т.е. ряда значений Хi принимаемых случ величиной Х в N независимых опытах.

Состоятельная оценка – оценка, кот при увеличении объема выборки стремится по вероятности к истинному значению числовой хар-ки.

Несмещенная – оценка, мат ожидание кот = оцениваемой числовой характеристике.

Точечная оценка дисперсии D(X)=1/(n-1)*Σ(Хi-Xср)2

Точечная оценка – выражается одним числом, она должна быть состоятельной, несмещённой, эффективной.

21. Интервальные оценки законов распределения.

Важно не только получить точечную оценку, но и определить доверительный интервал, кот задается доверительной вероятностью: Р{Хн<Х<Хв}=r-q

q – уровень значимости

Хн, Хв – ниж и верх границы интервала.

Под р%-м квантилем Хр понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна р% (рис).

На основании такого подхода вводится понятие квантильных значений погрешности, т.е. значение погрешности, заданной доверительной вероятностью Рх границ интервала неопределенности. Для получения интервальной оценки норм распределения случ величины необходимо:

1. определить……………………………………………………………………

2. выбрать довер вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99

3. найти границы: F(Хв)=q/2=1-р/2, F(Хн)=1-q/2=1+р/2

Д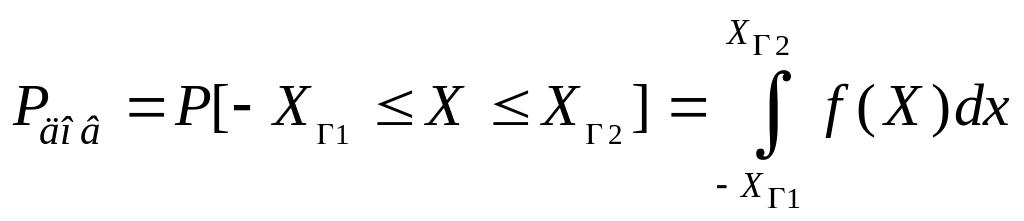 оверительная вероятность – вероятность того, что случайная величина попадёт в границы доверительного интервала.

Интервальная оценка – это способ оценки случайной величины, который с заданной степенью достоверности включает в себя значения оцениваемого параметра. Здесь определяется доверительный интервал, между границами которого с определенной доверительной вероятностью P находится истинное значение.