Лабораторная работа № 2

Изучение молекулярно-механического трения при сухом и граничном режимах

Цель работы: изучить экспериментальную и теоретическую методики определения коэффициента трения при качении с проскальзыванием стальных образцов типа диск–диск.

Основные задачи работы.

1. Ознакомиться с назначением, устройством и принципом работы машины трения СМТ–1.

2. Изучить порядок работы при испытании образцов.

3. Изучить экспериментальную и теоретическую методики определения коэффициента трения.

4. Провести испытания и определить коэффициент трения по условиям эксперимента для режимов сухого и граничного трения.

5. Провести испытания и построить графическую зависимость коэффициента трения от скорости скольжения.

6. Провести испытания и для ряда значений нагрузок построить зависимость коэффициента трения от нагрузки и от контурного давления.

7. Рассчитать теоретические значения коэффициента трения для приработанных образцов и сравнить с экспериментальными значениями.

8. Оформить отчет о лабораторной работе на листах формата А4.

Введение

Качение с проскальзыванием реализуется в зубчатых передачах, кулачковых механизмах, подшипниках качения, обгонных муфтах и в других узлах трения автомобиля.

Режим сухого трения – внешнее трение без смазочного материала.

Режим граничного трения – внешнее трение при наличии на поверхностях трения граничного слоя смазки квазикристаллической структуры толщиной до 0,1 мкм. Поляризованные молекулы смазки ориентируются вертикально под действием переменного электрического поля, генерируемого поверхностным слоем атомов твердого тела. Как правило, граничный слой смазки образует несколько слоев молекул, причем связь молекул с поверхностью с увеличением числа слоев ослабевает и становится настолько малой, что тепловые колебания молекул не позволяют создать какую-либо упорядоченную структуру. Граничный слой в нормальном к поверхности направлении выдерживает огромные напряжения, сопоставимые с прочностью материала поверхности твердого тела, и практически не сопротивляются касательным напряжениям. Сдвиговое сопротивление молекулярной связи (при граничном режиме трения) мало и коэффициент трения примерно на порядок меньше коэффициента трения при трении без смазочного материала. Адсорбция молекул смазочного материала на металлической поверхности протекает с большой скоростью, поэтому граничная пленка обладает свойством восстановления. При недостатке смазки на образование граничного слоя трение переходит в режим сухого трения, при этом коэффициент трения увеличивается в 2...10 раз [1].

Внешнее трение имеет молекулярно-механическую природу. Одним из основных источников диссипации энергии при трении является работа, затрачиваемая на формирование и разрушение молекулярных связей, которые образуются на пятнах касания микронеровностей шероховатых поверхностей трения. Обычно молекулярное взаимодействие обусловлено Ван-дер-ваальсовыми силами [2].

Молекулярная составляющая коэффициента трения рассчитывается по формуле [2]

(1)

где – фрикционные параметры, характеризующие физико-хими-ческое состояние поверхности трения: – удельное сдвиговое сопротивление молекулярной связи; – пьезокоэффициент молекулярной составляющей силы трения; – фактическое давление на пятнах контакта шероховатых поверхностей. Значения , а также для некоторых материалов приведены в табл. 1 [3].

Таблица 1

Величина молекулярной составляющей коэффициента трения и фрикционных параметров и для режима сухого трения неприработанных поверхностей трения

Материал
Свинец	33	0,140	2,74	0,057
Хром	1000	0,135	15	0,12
Медь	520	0,115	18,2	0,08
Титан	1280	0,100	28,2	0,078
Олово	44	0,170	4,49	0,068
Фторопласт	31	0,028	3,41	0,017
Резина	–	–	2,5	0,010
Сталь 30ХГСА	3400	0,125	200,6	0,066
Сталь 45	2700	0,119	203,9	0,044
Сталь 45	3240	0,112	129,6	0,072
Сталь 40Х	3410	0,109	184,1	0,055
Сталь 08Х18Н9Т	1590	0,15	31,8	0,130

Значения и зависят от скорости относительного перемещения образцов, степени их очистки от всевозможных загрязнений и адсорбированных на поверхностях пленок. На приработанных поверхностях всегда имеются пленки и загрязнения, поэтому величины и необходимо определять для реальной пары трения в условиях ее работы [4].

Механическая составляющая силы трения расходуется на процессы деформирования тонких поверхностных слоев трущихся тел. Объем материала, втянутого в деформацию, определяется величиной взаимного внедрения микронеровностей поверхностей трущихся тел, которое может значительно превосходить толщину «третьего тела». Механическая составляющая силы трения определяется характером напряженно-деформированного состояния материала на пятнах контакта.

Механическая составляющая коэффициента трения для элементарной фрикционной связи рассчитывается для пластического и упругого контакта по следующим формулам [2]:

, (2)

, (3)

где – относительное внедрение микронеровности; – глубина внедрения; – радиус кривизны микронеровности; – коэффициент гистерезисных потерь при скольжении единичной микронеровности; – коэффициент гистерезисных потерь при одноосном растяжении-сжатии (табл. 2).

Таблица 2

Значения коэффициента гистерезисных потерь [3]

Материал		Материал
Медь Фосфористая бронза Дюралюминий	0,04 0,04 0,03	Закаленная сталь Пластмасса Резина	0,02 0,08...0,12 0,09...0,13

Процессы молекулярного взаимодействия ограничиваются «третьим телом», т.е. протекают в пленке и распространяются на глубину порядка сотых долей микрона. Процессы механического взаимодействия происходят в самом твердом теле в слоях толщиной от десятых долей микрона и выше. Это различие в уровнях взаимодействий позволяет провести их суммирование и определить суммарную силу трения и коэффициент:

(4)

Тогда суммарный коэффициент трения для единичной микронеровности будет определяться по формуле

(5)

где – для единичной микронеровности при пластическом контакте; – при упругом.

Для нахождения суммарной силы трения шероховатых тел необходимо просуммировать силы трения на всех единичных фрикционных контактах.

Если не рассматривать процесс приработки, в течение которого изменяется технологическая шероховатость, то при испытаниях на трение и износ мы будем иметь дело с равновесной шероховатостью, которая при неизменных скорости и нагрузке имеет вполне конкретное значение и воспроизводится. Коэффициент трения будет иметь минимальное значение при заданных значениях скорости вращения, нагрузки и температуры поверхностей трения.

В зависимости от контурного давления в зоне контакта образцов различают следующие четыре вида контактного взаимодействия [5].

1. Упругий ненасыщенный контакт.

2. Упругий насыщенный контакт.

3. Пластический ненасыщенный контакт.

4. Пластический насыщенный контакт.

Упругий контакт имеет место, когда максимальные напряжения на наиболее внедренной микронеровности меньше твердости по Бринелю менее жесткого элемента пары трения. Реализуется для приработанных поверхностей узлов трения и материалов с низким значением модуля упругости, например, резины.

Пластический контакт имеет место, когда средние нормальные напряжения в зонах касания неровностей достигают значений твердости по Бринелю деформируемого материала.

Ненасыщенный контакт имеет место, когда число контактирующих неровностей меньше числа неровностей на контурной площади контакта.

Насыщенный контакт – число контактирующих неровностей равно их числу на контурной площади контакта [3].

Сумма величин реакций на фактических пятнах контакта в любой момент времени равна действующей силе на узел трения. Если нагрузка на отдельном фактическом пятне контакта превосходит твердость по Бринелю более мягкой поверхности узла трения, то происходит увеличение фактической площади контакта микровыступа (за счет его пластической деформации и износа) до тех пор, пока деформации станут упругими. Следовательно, после приработки определяющими будут упругие деформации микровыступов шероховатой поверхности, причем зона этих деформаций будет лежать на границе упругих и пластических деформаций микровыступов поверхностей узла трения.

В лабораторной работе будет изучаться коэффициент трения приработанных поверхностей образцов, поэтому будет рассматриваться только упругий ненасыщенный контакт, который реализуется и является основным для металлической пары трения в период после приработки вплоть до начала катастрофического износа.

Формулы для расчета коэффициента трения при упругом ненасыщенном контакте имеют следующий вид [5]:

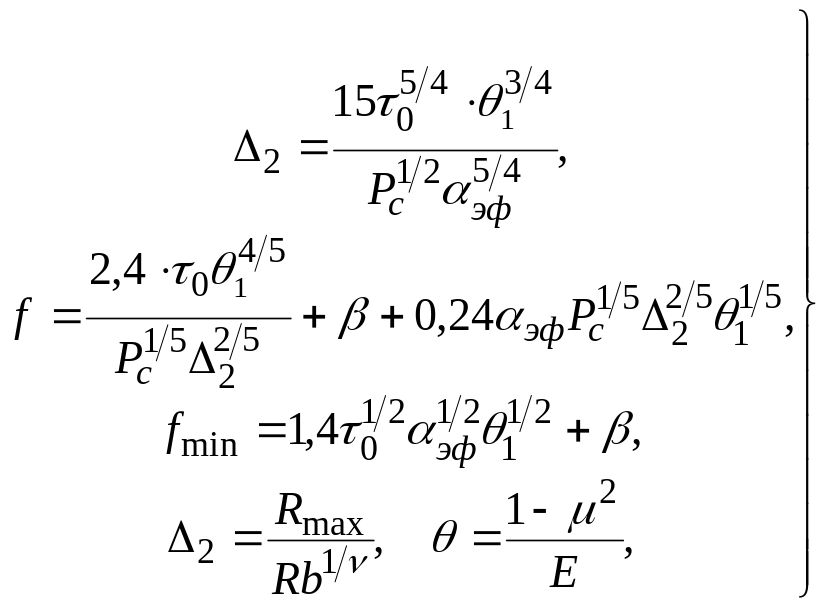(6)

где – комплексный параметр шероховатости более твердой поверхности; – контурное давление; – коэффициент эластичности Кирхгоффа более мягкой поверхности; – максимальное значение шероховатости; – средний радиус вершин микронеровностей; – параметры кривой опорной поверхности; – коэффициент Пуассона; – модуль упругости Юнга; – минимум коэффициента трения реализуется для приработанной поверхности обычно при упругом или упругопластическом контакте.

Для приработанных поверхностей трения, при условии, что деформирование микровыступов будет находиться на границе упругопластической области деформаций и учитывая, что комплексный параметр шероховатости изменяется на этой границе монотонно, получим [5]

, (7)

где определяется по формуле (6), а согласно [5]

. (8)

Из условия (7) получается формула для расчета прочности молекулярной связи на срез

. (9)

Формула (9) верна только для случая фиксированных в ходе опыта нормальной нагрузки на образцы, скорости скольжения и теплового режима после приработки. Для соблюдения этих условий в опыте приработка ведется в течение 5000 циклов, что в 2,5 раза выше рекомендуемого значения [2].

В данной лабораторной работе будет изучаться внешнее трение приработанных образцов типа диск-диск при качении с проскальзыванием. Образцы прижимаются друг к другу внешней силой , величина которой задается и контролируется. Схема взаимодействия образцов показана на рис. 1. Контакт образцов осуществляется по образующей дисков на контурной площади , представляющей собой прямоугольник длиной (толщина узкого образца) и шириной . Ширину зоны контакта можно определить, используя решения Герца [3] для упругого контактирования гладких цилиндров с параллельными осями:

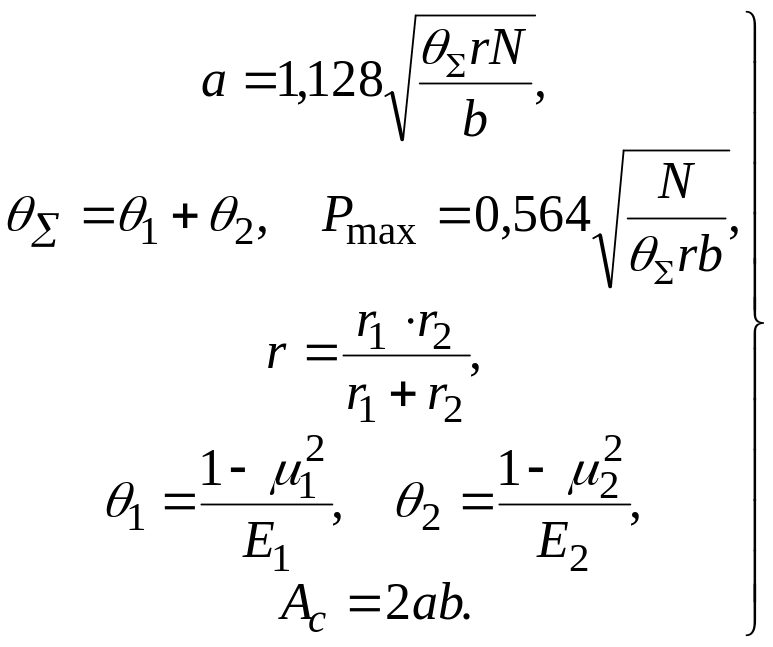(10)

Здесь – половина ширины площадки зоны контакта; – коэффициент эластичности для случая контакта двух деформируемых тел; – коэффициенты эластичности материала образцов; – прижимающая образцы нагрузка.

Средняя величина контурного давления определяется по формуле

(11)

Контакт упругий, если более мягкого образца. Пластические деформации в зоне контакта образцов появятся, если (см. рис. 1) превысит значение твердости материала более мягкого образца. Предельным режимом нагружения будет сила

, (12)

приводящая к макроскопическому деформированию более мягкого образца. Для образцов, используемых в лабораторной работе, Н.

Момент трения определяется по формуле

(13)

где – радиус нижнего образца; – сила трения определяется по известному значению нагрузки

(14)

Момент трения и нагрузка на образцы контролируются в ходе эксперимента. Зная экспериментальные значения и можно рассчитать экспериментальное значение суммарного коэффициента трения

(15)

и сравнить его с теоретическим значением, рассчитанным по формулам (6).

Взаимодействие твердых тел при упругих деформациях является наиболее характерным для металлов, имеющих поверхности с шероховатостью . С увеличением нагрузки фактическое давление изменяется незначительно, так как увеличивается площадь контакта. Для приработанных поверхностей фактическое давление на микровыступах зоны контакта определяется по формуле [5]

, (16)

где – прочность молекулярной связи на срез для приработанной поверхности определяется по формуле (9).

Для приработанной поверхности более твердого образца, обозначенного цифрой 2, комплексный параметр шероховатости определяется по формуле (8) или (6), а также может быть определен экспериментально, для чего необходимо измерить на профилографе-профилометре и воспользоваться формулой [5]

. (17)

Напряжения среза образующихся при трении молекулярных связей можно найти из опыта по формуле

, (18)

где фактическая площадь контакта

. (19)

Скорость скольжения (проскальзывания при качении образцов типа диск-диск) определяется по формуле

, (20)

где – коэффициент проскальзывания; – частота вращения нижнего образца (2), .

Мощность сил трения скольжения

, Вт. (21)

Тепловой поток в образцы в зоне контакта

. (22)

Пьезокоэффициент определяется следующим образом

. (23)