3. Средние величины

Для того, чтобы количественно охарактеризовать самые существенные свойства распределения, а также для того, чтобы можно было сравнить разные распределения, вычисляют средние показатели - выборочные числовые характеристики.

В статистике используются различные величины в зависимости от того, какие цели при анализе материала ставит исследователь. Понятием средней величины пользуемся в тех случаях, когда требуется определить средний надой по стаду, средний привес, средний прирост стада, средние клинические показатели деятельности сердца, лёгких, среднего состава крови и во многих других случаях.

Различают следующие виды средних величин: средняя арифметическая ( ), средняя геометрическая ( ), средняя квадратическая ( ), средняя гармоническая ( ) , мода (М₀) и медиана Ме.

Наиболее распространенным видом средних величин является средняя арифметическая, которая бывает простой и взвешенной.

3.1. Средняя арифметическая

Средняя арифметическая является наиболее распространенной среди средних величин. Ее применяют в тех случаях, когда даны отдельные объекты с индивидуальными значениями признаков, выраженными абсолютными показателями. Среднюю арифметическую определяют как отношение суммы индивидуальных значений признаков к их количеству.

Различают среднюю арифметическую простую и взвешенную. Среднюю арифметическую простую применяют в случае, если индивидуальные значения признака в совокупности встречаются по одному разу, а взвешенную  если индивидуальные значения признака представлены несколькими объ­ектами.

Среднюю арифметическую простую определяют по формуле:

,

где  средняя;

х  варианты;

n  число вариант.

Формула средней арифметической взвешенной имеет вид:

,

где f  частота вариант.

Рассмотрим методику расчета средней арифметической.

Пример. Имеются данные по 8 коровам об их удое за год (табл. 3).

Т а б л и ц а 3

Удой коровы

№ коровы	Удой коровы за год, кг
	х
1 2 3 4 5 6 7 8	3811 3600 3480 3758 4059 4222 4160 3971
Итого

Требуется определить средний удой на одну корову за год.

Так как даны индивидуальные значения удоя молока по каждой корове, то средний удой определяется по формуле средней арифметической простой:

кг.

Таким образом, среднегодовой удой от коровы за год составляет 3883 кг.

Технология решения задачи в табличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис.27

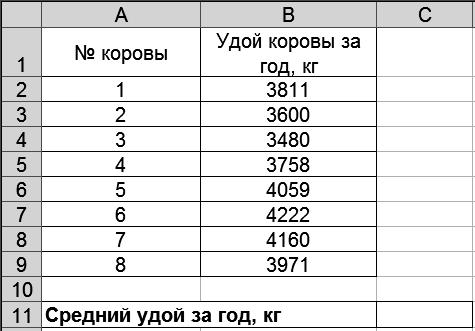
Р и с. 27

2. Рассчитайте средний удой на корову за год как среднюю арифметическую простую.

2.1. Выделите ячейку С11.

2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, f_x Функция, щелкнув поочередно левой кнопкой мыши.

2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория  <Статистические>, Выберете функцию  <СРЗНАЧ> (рис. 28).

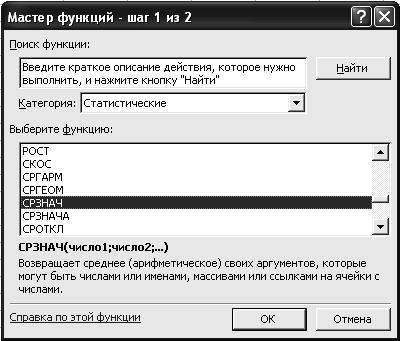
Р и с. 28

2.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

2.5. На вкладке СРЗНАЧ установите параметры в соответствии с рис. 29.

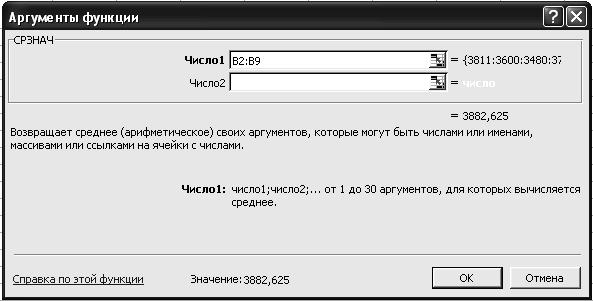
Р и с. 29

2.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 30).

Р и с. 30