9.2. Корреляционная зависимость. Коэффициент корреляции.
Зависимость между значениями одной случайной величины и условным средним значением другой случайной величины носит название корреляционной (от англ. correlation - согласование, связь, взаимосвязь, соотношение, взаимозависимость); термин впервые введен Гальтоном в 1888г.
Парный коэффициент корреляции Пирсона (1896 г.) изменяется в пределах от -1 до +1. Значение 0,00 интерпретируется как отсутствие корреляции. Корреляция определяет степень, с которой значения двух переменных пропорциональны друг другу.
Рабочие формулы коэффициентов корреляции применяют с учетом того, с какой выборкой (большей или малой) мы имеем дело.
Например, для малых выборок удобнее всего пользоваться следующей формулой:
(
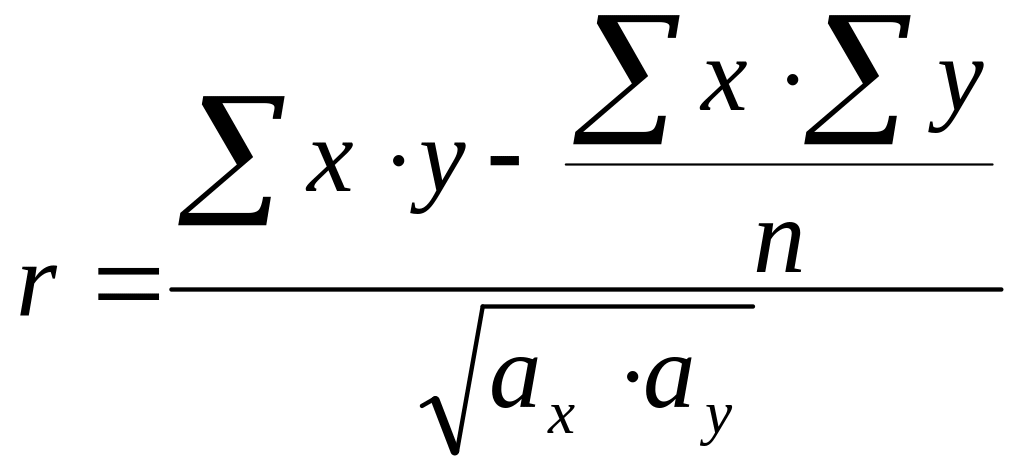или
),
где
и
,
где х-варианты первого признака;
у-варианты второго признака; n-число наблюдений в выборке.
Вспомогательная таблица для расчетов коэффициента корреляции.
№ |
X |
Y |
XY |
X2 |
Y2 |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
… |
|
|
|
|
|
|
= |
= |
= |
= |
= |
=
Коэффициент корреляции, возведенный в квадрат, называется коэффициентом детерминации r2. Он показывает долю изменений, которые вызваны факторным признаком. Коэффициент детерминации r2 является прямым способом выражения зависимости одного признака от другого. Если известно, что У находится в причинной связи с Х, то r2 – это доля вариации У, обусловленная влиянием Х.
Для
изучения корреляционных связей большое
значение имеет коэффициент регрессии
,
который показывает, насколько в среднем
изменяется признак (Х), если коррелирующий
с ним признак (У) изменяется на определенную
величину.
Формула для расчета коэффициента имеет вид:
;
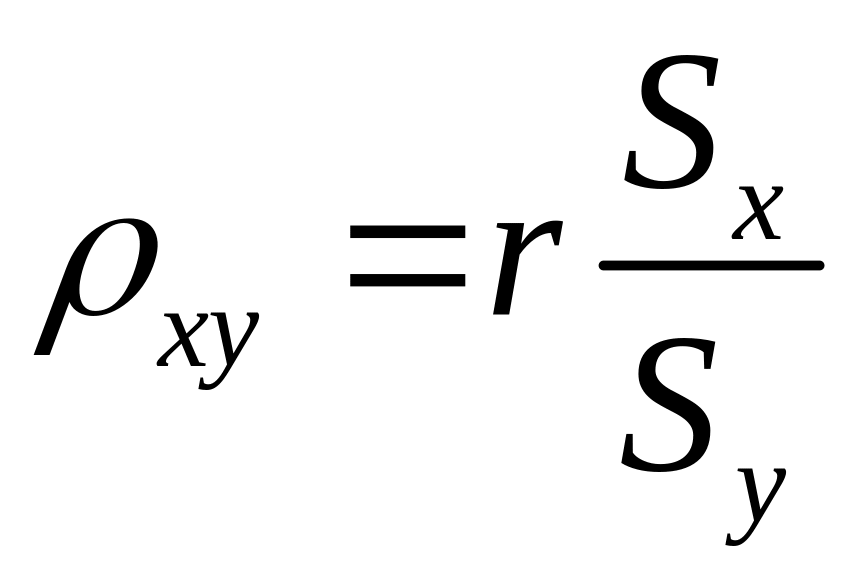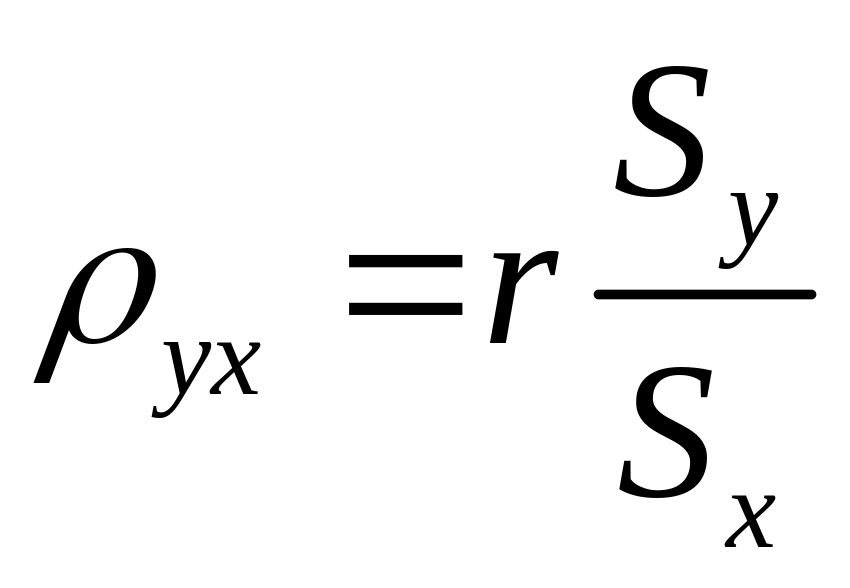
Корреляционные зависимости наблюдаются между очень многими признаками организмов – морфологическими, физиологическими, а также между различными биологическими процессами. Различают положительную и отрицательную корреляции. При положительной корреляции с увеличением одного признака увеличивается и другой. Например, с увеличением живой массы коров первотёлок возрастает и удой; чем выше процент жира в молоке, тем выше и процент белка в нём. При отрицательной корреляции с увеличением удоя у коров снижается жирность молока; куры с высокой яйценоскостью имеют более мелкие яйца.
В зоотехнической и ветеринарной практике изучение корреляционной зависимости имеет большое значение. Так, например, для животновода очень важно знать, какова связь между средним удоем за лактацию и процентом жира в молоке, иначе говоря, дают ли более высокоудойные коровы молоко с повышенным содержанием жира или, наоборот, с пониженным и насколько часто встречаются исключения из той или другой зависимости. Или другой пример: из-за отрицательной корреляционной зависимости между высокой молочностью и способностью к откорму невозможно выведение породы, сочетающую высокую молочную продуктивность и высокие мясные качества; между устойчивостью к эймериозу у кур и массой тела существует положительная корреляция, поэтому, чем более упитанные куры, тем менее они предрасположены к заболеванию.