Лабораторная работа №2

(продолжительность 4 часа)

Тема: Транспортная логистика

Цель работы: Освоение методов выбора перевозчика, определение оптимальных параметров транспортирования готовой продукции, составление оптимального плана перевозок

Предварительная подготовка заключается в изучении студентами теоретического материала по следующим разделам:

• Цель транспортной логистики.

• Состав транспортных систем. Классификация транспорта.

• Виды перевозок. Альтернативы перевозок и критерии выбора транспортных посредников. Терминальные перевозки.

• Транспортные издержки и тарифы.

• Организация и управление транспортировкой.

• Математические методы, используемые для оптимизации перевозок.

Вопросы для самоконтроля подготовленности к занятию:

1. Цель и задачи транспортной логистики.

2. Какие проблемы транспортирования существуют в современной логистике?

3. Что такое транспортная система?

4. Какие критерии используют при выборе транспорта?

5. Каков состав транспортных издержек?

6. Назовите цели и ограничения «транспортной» задачи.

Литература, рекомендуемая для подготовки к занятию: [1],[22],[8]

Обеспечение работы: у каждого студента стандартный набор канцелярских принадлежностей, тетрадь для лабораторных работ или писчая бумага и стиплер, а также черновая бумага. Для обеспечения работы всей группы

потребуется аудиторная доска с мелом.

Общие требования к проведению и оформлению работы: Работа проводится в течение 4 аудиторных часов. Каждый студент выполняет лабораторную работу индивидуально. Результаты выполнения каждого задания оформляются в виде самостоятельного раздела отчета сразу же на занятии.

Содержание и порядок выполнения лабораторной работы:

Лабораторная работа №2 так же выполняется поэтапно. На первом этапе студентам предстоит найти начальное решение транспортной задачи, путем разработки матрицы перевозок от m поставщиков к n потребителям с наименьшими суммарными затратами на транспортировку.

В общем случае транспортная задача рассматривается как разработка наиболее экономичной структуры перевозки однотипной продукции из нескольких пунктов отправления в несколько пунктов назначения. Величина транспортных расходов задается с помощью тарифов на перевозку единицы груза. Транспортную задачу можно представить в виде сети с n пунктами отправления и m пунктами назначения.

1

a₂

a_n n m

На приведенной иллюстрации используются следующие обозначения:

- а_1, … , а_n – объемы предложений;

- b₁, …, b_m – объемы спроса;

- с_i,j – стоимость перевозки единицы груза из пункта i в пункт j;

- х_i,j – объем перевозки единицы груза из пункта i в пункт j.

Цель задачи – найти план перевозок Х=(х_i,j), который минимизирует суммарные затраты. Приведем математическую модель транспортной задачи:

при ограничениях

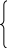
, i = 1, …, n,

, j = 1, … , m,

х_i,j  0, i = 1, …, n; j = 1, … , m.

Для решения транспортной задачи исходные данные удобно представлять в виде матрицы планирования.

Пункты предложения	Пункты назначения				Предложение (ед. продукции)
	1	2	...	m
1	с1,1 х1,1	с1,2 х1,2	…	с1,m x1,m	a1
2	c2,1 x2,1	c2,2 x2,2	…	c2,m x2,m	a2
…	…	…	…	…	…
n	cn,1 xn,1	cn,2 xn,2	…	cn,m xn,m	an
Спрос (ед.продукции)	b1	b2	…	bm

В соответствии с приведенной математической моделью, имеет место равенство суммарных предложения и спроса:

.

Очевидно, в реальности такая ситуация встречается далеко не всегда. Однако для решения любой транспортной задачи следует добиться этого равенства искусственно или специальным образом. Если данное равенство выполняется, то такая задача называется сбалансированной (закрытой), в противном случае – несбалансированной (открытой). В том случае, если исходная транспортная задача не является сбалансированной, ее следует сбалансировать, то есть привести к закрытой форме. Для этого необходимо ввести фиктивные пункты назначения или предложения.

В ситуации, когда суммарное предложение превышает суммарный спрос, необходимо ввести фиктивный (реально не существующий) пункт назначения, который будет формально потреблять излишнее предложение:

Пункты предложения	Пункты назначения					Предложение ед. продукции
	1	2	...	m	Фиктивный
1	с1,1 х1,1	с1,2 х1,2	…	с1,m x1,m	сф xф1,m	a1
2	c2,1 x2,1	c2,2 x2,2	…	c2,m x2,m	сф xф2,m	a2
…	…	…	…	…	…	…
n	cn,1 xn,1	cn,2 xn,2	…	cn,m xn,m	сф xфn,m	an
Спрос ед.продукции	b1	b2	…	bm	bф

Стоимость доставки единицы груза из любого пункта предложения в фиктивный пункт назначения принимают равной 0: с_ф = 0.

Если суммарный спрос превышает суммарное предложение, то вводят фиктивный пункт предложения, который формально восполняет недостаток предложения:

Пункты предложения	Пункты назначения				Предложение ед. продукции
	1	2	...	m
1	с1,1 х1,1	с1,2 х1,2	…	с1,m x1,m	a1
2	c2,1 x2,1	c2,2 x2,2	…	c2,m x2,m	a2
…	…	…	…	…	…
n	cn,1 xn,1	cn,2 xn,2	…	cn,m xn,m	an
Фиктивный	сф хфn,1	сф хфn,2		сф хфn,m	аф
Спрос ед.продукции	b1	b2	…	bm

Стоимость доставки единицы груза из фиктивного пункта предложения в любой пункт назначения принимают равной 0: с_ф = 0.

Решение транспортных задач проводится в два этапа: первоначальный и основной. На первоначальном этапе получают допустимое базисное решение, которое также называют опорным планом перевозок. Допустимое базисное решение удовлетворяет всем условиям задачи, кроме оптимальности. Опорный план перевозок предполагает выполнение не более чем m + n – 1 поставок. Заметим, что m + n – 1 –это число линейно независимых ограничений в системе ограничений. Можно показать, что всегда найдется такое оптимальное решение транспортной задачи, в котором количество поставок (занятых клеток в матрице планирования) также не превосходит числа m + n – 1. Поэтому оптимальный план перевозок ищут среди опорных планов.

Для нахождения первоначального решения используют методы северо-западного угла, наименьшей стоимости, Фогеля и др. Все эти методы предполагают решение одной задачи – построение начального опорного плана. Однако качество начального решения зависит от того, какой метод был использован для его получения. Как правило, метод северо-западного угла (очень простой в применении) дает решение более далекое от оптимального плана поставок по сравнению с методами наименьшей стоимости и метода Фогеля.

На основном этапе проводится последовательное улучшение начального опорного плана перевозок. В результате получается оптимальное базисное решение (оптимальный план перевозок), которое является окончательным результатом для поставленной транспортной задачи. На основном этапе применяются распределительный метод, метод потенциалов и др.