Разработка алгоритма
Перед сортировкой массив Nums должен быть заполнен целыми числами от 1 до m, обозначающими начальный порядок строк исходной матрицы. Сортировка выполняется методом пузырька.
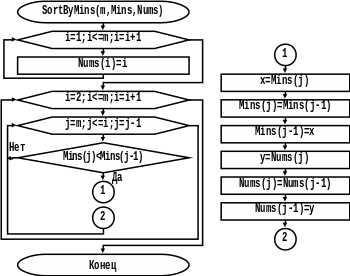
Рисунок 14. Схема алгоритма процедуры сортировки номеров строк в порядке возрастания минимальных значений.
Участок программы 1-2 включает в себя двукратное повторение однотипной последовательности действий, меняющих местами значения переменных. Реализуя принцип восходящего программирования, заменяем однотипные последовательности подпрограммами. В этом случае локальные переменные x и y не используются.
Рисунок 15. Вызов подпрограмм, меняющих значения аргументов, из процедуры сортировки номеров строк.
Разработка исходного текста процедуры сортировки номеров строк в порядке возрастания минимальных значений.
Sub SortByMins(m As Long, Mins(), Nums() As Long)
Dim i As Long, j As Long
For i=1 To m 'Для всех строк
Nums(i)=i 'Записываем в Nums их номера
Next i
For i=2 To m 'Сортировка методом «пузырька»
For j=m To i Step -1 'Для всех пар с последней по i-ю
If Mins(j)<Mins(j-1) Then 'Если пара не отсортирована
Swap Mins(j),Mins(j-1) 'Меняем местами минимумы
Swap Nums(j),Nums(j-1) 'и номера строк, соответственно
End If
Next j 'следующая пара
Next i 'поиск следующего минимума
End Sub
Процедура замены значений переменных
Информационная структура
Входные данные
a, b – значения, которые надо поменять местами.
Локальные данные
c – промежуточное значение для замены.
Выходные данные
a, b – значения поменянные местами.
Разработка алгоритма
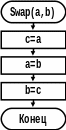
Рисунок 16. Схема алгоритма подпрограммы замены значений переменных.
Разработка исходного текста процедуры
Sub Swap (a,b)
Dim c
c=a
a=b
b=c
End Sub
Процедура сортировки матрицы
В массив с результатом требуется записать строки исходного массива, порядок которых определяется на предыдущем этапе.
Информационная структура
Входные данные
m – число строк матрицы – целое число >0;
n – число столбцов матрицы – целое число >0;
A – двумерный массив с исходной матрицей – числового типа.
Nums – одномерный массив упорядоченных номеров строк – целые.
Локальные данные
i – номер текущей строки массива – целое число от 1 до m;
j – номер текущего столбца массива – целое число от 1 до n;
Выходные данные
B – двумерный массив с отсортированной матрицей – числа.
Разработка алгоритма
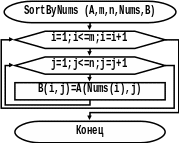
Рисунок 17. Схема алгоритма процедуры сортировки матрицы.
Разработка исходного текста процедуры
Sub SortByNums(A(),m As Long, n As Long, Nums() As Long,B())
Dim i As Long, j As Long
For i=1 To m 'Для всех строк
For j=1 To n 'Для всех элементов строки
B(i,j)=A(Nums(i),j) 'Записываем строки в порядке Nums
Next j 'Следующий элемент строки
Next i 'Следующий столбец
End Sub
2.3.4Пример 4. Решение системы линейных алгебраических уравнений (СЛАУ)
Необходимость решения СЛАУ возникает как в соответствующих задачах для непосредственного поиска результата, так и в составе более объёмных вычислительных задач, таких как интерполяция, решение систем дифференциальных уравнений, метод конечных элементов, и многих других.
Постановка задачи
Задание: получить численное решение СЛАУ.
СЛАУ представляется в матричном виде: AX=B. Исходными данными являются количество уравнений, главная матрица A и вектор свободных членов B. Результатом должен быть вектор решений X или сообщение о неопределённости или несовместности системы. Тип результата определяется в процессе решения и кодируется числом. Исходные данные считываются с текущего листа MS Excel, где расположим их следующим образом: в левой верхней ячейке – размер, начиная со следующей строки и первого столбца – матрица A, через столбец справа от неё – столбец B. Результат выведем в виде строки снизу от матрицы А.