3.11. Баланс мощностей

Для схемы на рис. 3.31 запишем уравнение по второму закону Кирхгофа .

Умножим левую и правую части уравнения на сопряженный комплекс тока

или

где    - результирующее реактивное сопротивление;

I²- квадрат модуля тока.

где - полная комплексная, активная и реактивная мощности источника питания.

где - активная и реактивная мощности, потребляемые элементами схемы. Таким образом, получили уравнение .

Два комплексных числа равны, если равны по отдельности их вещественные и мнимые части, следовательно данное уравнение распадается на два:

  .

Полученные равенства выражают законы сохранения активных и реактивных мощностей.

3.12. Согласованный режим работы электрической цепи. Согласование нагрузки с источником

В схеме на рис. 3.32 z_i, R_i, X_i - полное, активное и реактивное сопротивления источника ЭДС, z_н, R_н, X_н - полное, активное и реактивное сопротивления нагрузки.

А ктивная мощность может выделяться только в активных сопротивлениях цепи переменного тока.

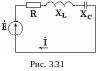
Активная мощность, выделяемая в нагрузке,

. (*)

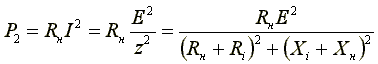Активная мощность, развиваемая источником ЭДС

. Коэффициент полезного действия для данной схемы:

.

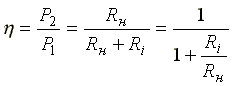Из формулы (*) видно, что выделяемая в нагрузке мощность будет максимальной, когда знаменатель минимален. Последнее имеет место при , т.е. при . Это означает, что реактивные сопротивления источника и нагрузки должны быть одинаковы по модулю и иметь разнородный характер. При индуктивном характере реактивного сопротивления источника реактивное сопротивление нагрузки должно быть емкостным и наоборот.

.

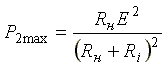Установим условие, при котором от источника к нагрузке будет передаваться наибольшая мощность.

.

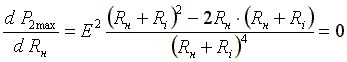Отсюда .

От источника к нагрузке передается наибольшая мощность, когда

.      .

Величина наибольшей мощности

.

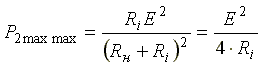Режим передачи наибольшей мощности от источника к нагрузке называется согласованным режимом, а подбор сопротивлений и - согласованием нагрузки с источником.

В согласованном режиме

.

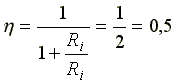Половина мощности теряется внутри источника. Поэтому согласованный режим не используется в силовых энергетических цепях. Этот режим используют в информационных цепях, где мощности могут быть малыми, и решающими являются не соображения экономичности передачи сигнала, а максимальная мощность сигнала в нагрузке.

23