3.10. Параллельное соединение резистора, катушки индуктивности, конденсатора в цепи гармонического напряжения

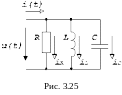
Рассмотрим схему, представленную на рис..25. Все ее элементы соединены параллельно и находятся под одним и тем же напряжением u(t)=U_msin(_u). Необходимо определить ток в цепи i(t). На основании 1-го закона Кирхгофа в любой момент времени справедливо соотношение

i(t)=i_R(t)+i_L(t)+i_C(t)

или

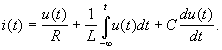
Подставив вместо u(t) гармоническую функцию времени и проведя необходимые математические операции, получим

Из уравнения видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90^o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90^o.

Будем определять искомый ток в виде i(t)=I_m=I_msin(ωt+ψ_i). Перейдем к комплексным мгновенным значениям

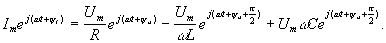Сокращая на e^{jw t} и учтя, что , получим

или

Выражение в скобках – комплексная проводимость цепи – резистивная составляющая проводимости, – реактивная составляющая проводимости.

Построим векторные диаграммы, соответствующие комплексному уравнению.

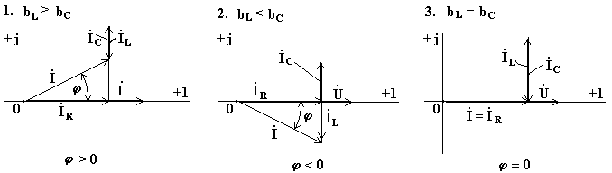Рис. 3.26                            Рис. 3.27                              Рис. 3.28

В схеме на рис. 3.25 может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением.

Из условия возникновения резонанса тока получим формулу для резонансной частоты тока

В режиме резонанса тока полная проводимость цепи - минимальна, а полное сопротивление z = 1/y- максимально. Ток в неразветвленной части схемы I=U/z в резонансном режиме имеет минимальное значение. В идеализированном случае R = 0, и z = 1/y.

Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр - пробкой.

Закон Ома в комплексной форме для амплитудных значений или для действующих значений .

Таким образом при параллельном соединении ветвей цепи комплексная эквивалентная проводимость равна сумме комплексных проводимостей ветвей:

3.10. Мощность в цепи синусоидального тока

Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.

Пусть мгновенные напряжение и ток определяются по формулам:

     

Тогда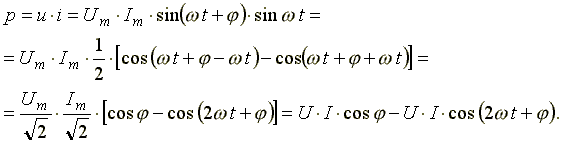  

Среднее значение мгновенной мощности за период

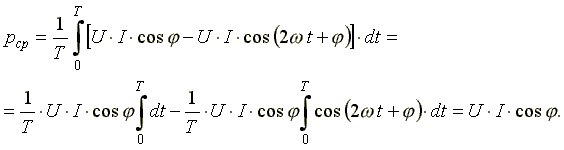
     Из треугольника сопротивлений (hbc/ 3/29) а .

П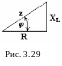 олучим еще одну формулу:

.

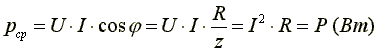Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P. Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию.

Возьмем реактивный элемент (индуктивность или емкость). Активная мощность в этом элементе , так как напряжение и ток в индуктивности или емкости различаются по фазе на 90^o. В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов. Происходит обратимый  процесс в  виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.

Преобразуем выражение

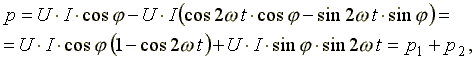
где - мгновенная мощность в активном сопротивлении;

- мгновенная мощность в реактивном элементе (в индуктивности или в емкости).

Максимальное или амплитудное значение мощности p₂ называется реактивной мощностью (Вар), sinφ = x/z.

Здесь x - реактивное сопротивление (индуктивное или емкостное).

Реактивная мощность, измеряемая в вольтамперах реактивных, расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.

Амплитудное значение суммарной мощности p = p₁ + p₂ называется полной мощностью.

Полная мощность, измеряемая в вольтамперах, равна произведению действующих значений напряжения и тока:

      ,

где z - полное сопротивление цепи.

Полная мощность характеризует предельные возможности источника энергии. В электрической цепи можно использовать часть полной мощности P = UIcosφ = Scosφ, где - коэффициент мощности или "косинус "фи".

Коэффициент мощности является одной из важнейших характеристик электротехнических устройств. Принимают специальные меры к увеличению коэффициента мощности. Возьмем треугольник сопротивлений и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 3.30).

     Из треугольника мощностей получим ряд формул:

,      , , .

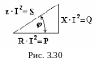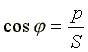При анализе электрических цепей символическим методом используют выражение комплексной мощности, равное произведению комплексного напряжения на сопряженный комплекс тока.

Для цепи, имеющей индуктивный характер (R-L цепи)

,

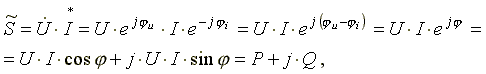где - комплекс напряжения; - комплекс тока; - сопряженный комплекс тока; - сдвиг по фазе между напряжением и током.

, так как в R-L цепи, напряжение опережает по фазе ток.

Вещественной частью полной комплексной мощности является активная мощность. Мнимой частью комплексной мощности - реактивная мощность.

Для цепи, имеющей емкостной характер (R-С цепи), . Ток опережает по фазе напряжение.

.

Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, - положительна, а в цепи с емкостным характером - отрицательна.