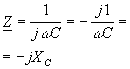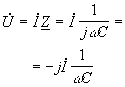3 .7. Прохождение гармонического тока через конденсатор

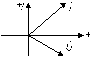
Рассмотрим линейный конденсатор емкостью С (рис. 3.17), через который протекает ток i(t)=I_msin( t+_i). Определим напряжение на конденсаторе. Связь между мгновенными значениями тока в конденсаторе и напряжения на нем определяется соотношением (2.4.6). Тогда

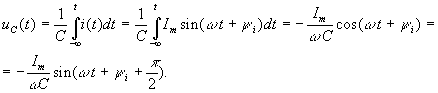
Дополнительный угол возник при переходе от косинусоидальной функции к синусоидальной. Напряжение на конденсаторе будем определять в виде u(t)=U_msin( t+ _u). Тогда

.

Перейдем к комплексным мгновенным значениям

или

Сокращая на оператор поворота e^jwt и учитывая, что

, получим (*)

Легко видеть, что величина имеет размерность сопротивления – Ом.. Она называется комплексным сопротивлением конденсатора

Выражение (*) – закон Ома для конденсатора в комплексной форме – можно записать в обобщенном виде или

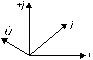
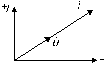
Из соотношения следует, что вектор напряжения на конденсаторе отстает от вектора тока в нем на (так как ). Векторная диаграмма тока и напряжения на конденсаторе показана на рис. 3.18. На рис. 3.19 показаны зависимости от времени тока, напряжения и мгновенной мощности (при y _i=0)

.

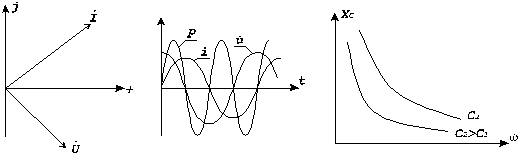
Рис. 3.18

Рис. 3.19

Рис. 3.20

Сравнение графиков мгновенной мощности для резистора, катушки индуктивности и конденсатора показывает:

• в резисторе мгновенная мощность всегда положительна, т.е. линейный резистор мощность потребляет;

• в конденсаторе (рис. 3.19) и в катушке мгновенная мощность может быть положительной (реактивный элемент запасает энергию) и отрицательной (реактивный элемент отдает энергию во внешнюю цепь).

Рассмотрим комплексное сопротивление конденсатора Величина называется емкостным сопротивлением конденсатора. Зависимости емкостного сопротивления от частоты w для двух значений емкости показаны на рис. 3.20. Емкостное сопротивление конденсатора на постоянном токе ( ) равно бесконечности и уменьшается до нуля с ростом частоты до бесконечности.

В табл. 3.2 приведена сводка основных соотношений, описывающих прохождение гармонического тока, через основные элементы цепи.

3.8. Закон Кирхгофа в комплексной форме.

1-й закон Кирхгофа: алгебраическая сумма токов в узле равна нулю. Например, для некоторого узла

i₁+i₂+i₃=0, (*)

где i₁, i₂, i₃ – токи в ветвях. Пусть каждый ток изменяется по синусоидальному закону:

i₁=I_m1sin(ωt+ψ₁); i₂=I_m2sin(ωt+ ψ₂); i₃=I_m3sin(ω+ ψ₃). (**)

Подставляя (**) в (*) и переходя к комплексным мгновенным значениям, получим + + =0

Таблица 3.2

Соотношение	Резистор	Катушка индуктивности	Конденсатор
Комплексное сопротивление
Реактивное сопротивление	–
Закон Ома
Векторная диаграмма

Сокращая это уравнение на оператор поворота и учитывая что амплитуды отдельных токов равны , , получим запись 1) для комплексных амплитуд

В общем случае, 1-й закон Кирхгофа для узла с n ветвями в комплексной форме имеет вид

.

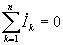В этом выражении токи, направленные к узлу, следует записать со знаком “плюс”, а направленные от узла – со знаком “минус” (или наоборот), а направление тока в ветви определяется произвольно.

Второй закон Кирхгофа в комплексной форме можно получить аналогично, записав все источники в ветвях в виде синусоидальных функций, напряжения на резисторах, на катушках индуктивности и на конденсаторах. Перейдя к комплексным мгновенным значениям и сократив уравнение на e^jwt, получим

,

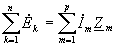где – алгебраическая сумма комплексных ЭДС источников напряжения. Со знаком плюс записываются те из них, положительные направления которых совпадают с выбранным направлением обхода контура; ЭДС, имеющие направления, противоположные обходу контура, записываются со знаком минус;

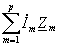– падение напряжений на комплексных сопротивлениях Z_m отдельных участков. Со знаком “плюс” берутся те, для которых направление тока совпадает с направлением обхода, а со знаком “минус” – те, для которых направление тока противоположно направлению обхода контура.

При составлении уравнений по второму закону Кирхгофа следует выбирать независимые контуры, не содержащие источников тока.