3.5. Прохождение гармонического тока через резистор

Рассмотрим резистор R (рис. 3.8), через который проходит синусоидальный ток i(t)=I_msin(t + _i). Надо определить напряжение на резисторе. Связь между мгновенными значениями напряжения и тока для линейного резистора устанавливает соотношение

u(t)=Ri(t)=RI_msin(t +  _i).

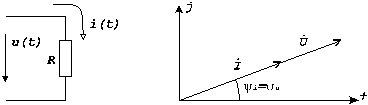
Рис. 3.8

Рис. 3.9

В общем случае напряжение будет изменяться по гармоническому закону т.е. в виде u(t)=U_msin(t +  _u).

u(t)=U_msin(t +  _u)=RI_msin(t +  _i).

Перейдем к комплексному мгновенному значению

Сокращая обе части уравнения на e^{jw t} получим . В левой части уравнения стоит комплексная амплитуда напряжения , а – комплексная амплитуда тока. Отсюда получаем . Это соотношение, устанавливающее связь между комплексной амплитудой напряжения на резисторе и комплексной амплитудой тока в нем, является записью закона Ома для резистора в комплексной форме. Если разделить ее правую и левую части на , получим то же соотношение для среднеквадратичных (действующих) значений

Из полученных соотношений следует вывод о том, что на резисторе ток и напряжение совпадают по фазе. Векторная диаграмма тока и напряжения на резисторе показана на рис. 3.9. На рис. 3.10 показаны зависимости от времени тока и напряжения на резисторе (при y _i=0). Обе синусоидальные функции совпадают по фазе.

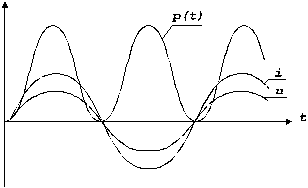
Рис. 3.10

Рассчитаем мгновенную мощность, выделяемую в резисторе

p(t)=u· i=U_msin t· I_msin t=U_mI_msin²  t .

По формулам тригонометрических преобразований выражение мгновенной мощности запишется в виде .

График мгновенной мощности показан на рис. 3.10. Мгновенная мощность изменяется с удвоенной частотой и всегда положительна, эта мощность расходуется в резисторе – выделяется в виде тепла. Рассчитаем среднее за период значение мощности, выделяющееся в резисторе

.

Учитывая связь между амплитудным и действующим значениями синусоидальных величин P=U· I.

3.6. Прохождение гармонического тока через катушку индуктивности.

Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L (рис. 3.11) протекает синусоидальный ток .

Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции

.

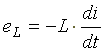Эта ЭДС уравновешивается напряжением, подключенным к катушке: u_L(t) + e_L = 0, и .

Е сли =1, то можно утверждать, что амплитуда напряжения на идеальной индуктивности . Разделив левую и правую части уравнения на , получим закон Ома для цепи с идеальной индуктивностью

где реактивное сопротивление индуктивности или индуктивное

Таким образом, ток в идеальной катушке индуктивности отстает по фазе от напряжения на ней на 90^o (рис.3.12), а индуктивное сопротивление пропорционально частоте (рис.3.13).

Мгновенная мощность:

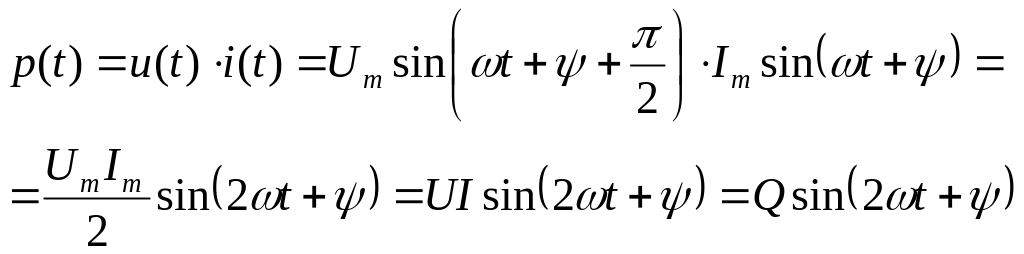
М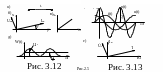 ощность называется реактивной и измеряется в вольт-амперах реактивных (ВАр). Средняя мощность равна нулю, т.е. рассеивание мощности или потери отсутствуют.

Напряжение на индуктивности в комплексной форме.

Так как напряжение на катушке:

,

то .

Единица измерения физической величины в левой части вольт, в правой – ампер, следовательно величина имеет единицы сопротивления – Ом. Поэтому, j = jw L называется комплексным сопротивлением катушки индуктивности.

Здесь - индуктивное сопротивление в комплексной форме.

Оператор 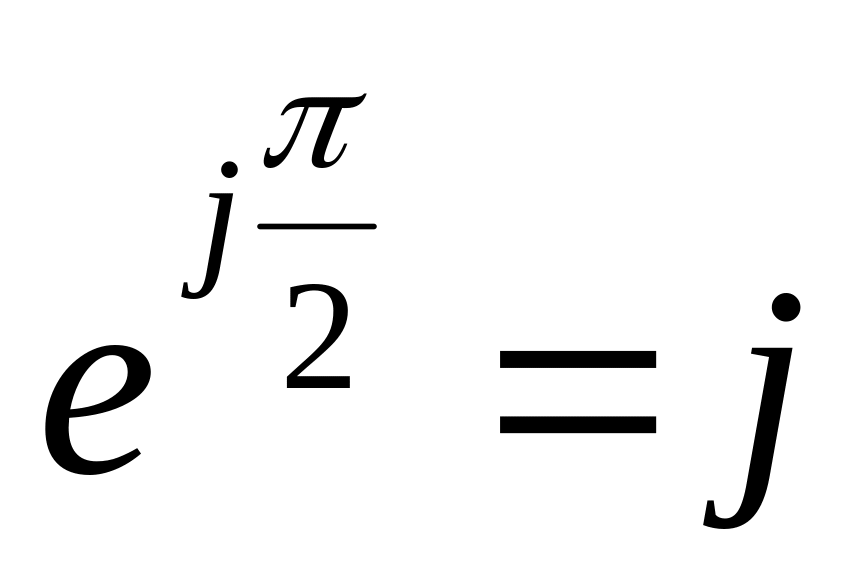отражает дифференцирование напряжения на индуктивности.

Векторы тока и напряжения на комплексной плоскости приведены на рис. 3.14.

Н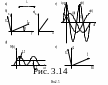 апряжение на реальной катушке индуктивности, имеющей активное сопротивление R, имеет следующий вид:

Анализ этого выражения показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0^o < φ < 90^o), величина которого зависит от соотношения R и L.

Это выражение в комплексной форме записи имеет вид:

(*)

где - полное комплексное сопротивление индуктивной катушки, z_L - модуль комплексного сопротивления, - начальная фаза комплексного сопротивления, - индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).

Полное сопротивление индуктивной катушки или модуль комплексного сопротивления

.

Комплексному уравнению (*) соответствует векторная диаграмма (рис. 3.15).

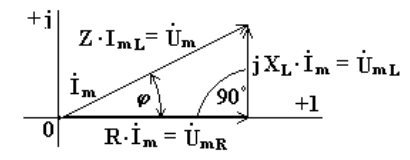Рис. 3.15

Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90^o. В цепи переменного тока напряжения на участках цепи складываются не арифметически, а геометрически. Если мы под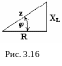 елим стороны треугольника напряжений на величину тока I_m, то перейдем к подобному треугольнику сопротивлений (рис. 3.16).

Из треугольника сопротивлений получим несколько формул: