2. Проектирование конечных автоматов

2.1. Проектирование конечного автомата без учета времени

Проектирование автоматов содержит следующие этапы:

– начальное задание функционирования;

– формализация задания;

– минимизация состояний;

– кодирование состояний;

– составление таблицы переходов;

– определение функций возбуждения элементов памяти;

– минимизация функций возбуждения элементов памяти;

– переход к выбранному базису элементов;

– составление логической схемы;

– создание макета и проверка автомата.

Начальное задание может иметь различную форму, в том числе и словесную. От нее переходят к формализованному заданию в виде таблиц, формул, временных диаграмм и т.п. Затем проводят минимизацию и кодирование состояний автомата, в результате получается таблица переходов, по которой можно найти функции возбуждения элементов памяти (триггеров).

Минимизация и кодирование состояний в общем случае достаточно сложная задача, но при проектировании узлов ЭВМ довольно часто она оказывается простой и ее решение подсказывается самой формулировкой задания на проектирование.

Обычно применяется двоичное кодирование состояний, при котором элементы памяти (триггеры) используются экономно.

Функции возбуждения триггеров, обеспечивающие переходы автомата из одного состояния в другое, реализуются его комбинационной частью. Они минимизируются и переводятся в заданный (выбранный) базис как обычно.

После получения функций возбуждения можно создать схему автомата и проверить ее моделированием.

Рассмотрим подробно методику создания автоматов, в которых в качестве элементов памяти применяются синхронные триггеры. Заметим, любой автомат можно построить на любом типе синхронных триггеров (RS, D, JK, T).

При двоичном кодировании состояний автомата число триггеров определяется по выражению

,

где N – число состояний автомата, – знак округления до ближайшего большего целого числа.

Пусть закон функционирования автомата определён и кодирование его состояний произведено. Значит, известна последовательность состояний триггеров, принимаемых ими в каждом такте под управлением входных сигналов x₁,x₂,…,x_k и текущего состояния Q₁, Q₂,…, Q_n. Следовательно, задача синтеза автомата сводится к получению функций возбуждения y_ij для каждого входа всех триггеров, обеспечивающих необходимые переходы автомата.

Функции выхода для автомата Мура зависят только от состояния автомата, поэтому

Z_i = Q_i.

Для автомата Мили функции выхода определяются как функции входных сигналов и состояний триггеров

Z_i = f(x₁,x₂,…,x_k,Q₁,Q₂,…,Q_n).

Все триггеры тактируются общим сигналом С, который после формирования функций возбуждения переводит триггеры в новое состояние.

Для нахождения функций возбуждения триггеров при синтезе автоматов применяют таблицы входов триггеров (табл. 1), по которым можно определить, какие сигналы надо подать на управляющие входы триггера, чтобы перевести его из одного состояния в другое. Эти таблицы называют также «словарями» триггеров, составляются они по таблицам переходов триггеров (табл. 2).

В табл. 1 приведены таблицы входов для JK–, RS– и D–триггеров. Построение таких таблиц рассмотрим на примере JK–триггера.

Представим таблицу переходов JK–триггера в развернутом виде (табл. 3).

Из этой таблицы следует, что для перевода триггера из состояния 0 в состояние 0 на JK–входы необходимо подать JK = 00 или JK = 01, т.е. для осуществления этого перехода состояние управляющего входа K безразлично. Условно операцию определения функций возбуждения для реализации перехода триггера из состояния 0 в состояние 0 можно записать так:

JK = 00 01 = 0–.

Для перевода JK–триггера из состояния 0 в состояние 1 на JK–входы необходимо подать комбинацию

JK = 10 11 = 1–.

Таблица 1

Таблица входов JK–, RS– и D–триггеров

Qt Qt+1	J К	R S	D
0 0	0 –	– 0	0
0 1	1 –	0 1	1
1 0	– 1	1 0	0
1 1	– 0	0 –	1

Таблица 2

Таблица переходов RS–, JK– и D–триггеров.

Вход 1	Вход 2	RS–триггер	JK–триггер	D–триггер
0 0 1 1	0 1 0 1	Qt 1 0 –	Qt 0 1 Qt’	0 0 1 1

Таблица 3

Qt	J	K	Qt+1
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	0

Для перевода JK–триггера из 1 в 0 должна быть подана комбинация

JK = 01 11 = –1,

а для перевода из 1 в 1

JK = 00 10= –0.

Аналогично получаются таблицы входов для RS–триггера и D–триггера (у D–триггера вход один).

Для определения функций возбуждения триггеров сначала строится совмещенная таблица переходов и входов вида табл. 4:

Таблица 4

Входы в момент времени t

Состояния триггеров

Необходимые сигналы на всех входах каждого триггера

Q (старое)

Qн (новое)

x1

x2

…

xk

Q1

Q2

…

Qn

Q1

Q2

…

Qn

y11

y12

…

yn1

yn2

Столбцы y₁₁, y₁₂,… ,y_n1, y_n2 определяют функции возбуждения триггеров (первый индекс – это номер триггера, второй индекс – номер входа триггера). Значения y_ij находят в таблице входов по значениям Q, Q_н (см. примеры проектирования).

Поскольку память любого автомата можно построить на любом типе триггеров, а комбинационную часть в любом базисе, то для любого автомата можно получить достаточно много вариантов схем.

Какой тип триггера выбрать? Чаще всего автоматы строят на JK и D триггерах. JK триггер имеет два входа (более развитую входную логику), поэтому для него функции возбуждения получаются проще, но их в два раза больше, чем у D триггера. Какой вариант будет лучше, заранее неизвестно. Чтобы найти решение, применяют метод проб и ошибок.

Пример 1.

Спроектировать автомат, работающий в двух режимах:

– при входном сигнале М = 0 он работает как двоичный трехразрядный счетчик (см. табл. 5),

– при М = 1 он работает как трехразрядный счетчик в коде Грея (см. табл. 5).

Таблица 5

№	Двоичный код			Код Грея
	Q2	Q1	Q0	Q2	Q1	Q0
0	0	0	0	0	0	0
1	0	0	1	0	0	1
2	0	1	0	0	1	1
3	0	1	1	0	1	0
4	1	0	0	1	1	0
5	1	0	1	1	1	1
6	1	1	0	1	0	1
7	1	1	1	1	0	0

Изменение управляющего сигнала М сразу приводит к изменению режима работы автомата, т.е. следующее состояние будет принадлежать другому коду.

Граф переходов автомата показан на рис. 2.

Выбор типа автомата и кодирование его состояний определяется здесь самой постановкой задачи. Это счетчик – значит, выходные сигналы снимаются с выходов триггеров соответствующих разрядов. А коль скоро это так, мы имеем здесь автомат Мура.

Пусть для реализации автомата выбраны JK–триггеры и базис И-НЕ.

Совмещенная таблица переходов и входов автомата приведена в табл. 6. В ней функции возбуждения элементов памяти (JK–триггеров) обозначены символами входов триггеров J и K с индексами – номерами соответствующих триггеров.

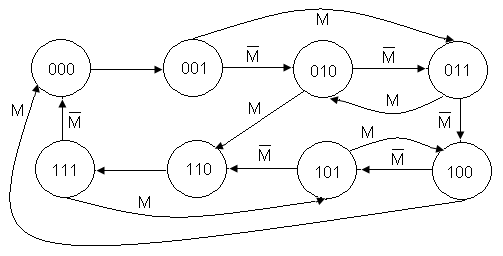
Рисунок 2 – Граф переходов автомата

Проведем минимизацию функций J и K с помощью карт Карно (табл. 7).

В результате получаем следующие функции:

J₂ = , K₂ = ,

J₁ = , K₁ = ,

J₀ = , K₀ = .

Преобразуем полученные функции к виду, удобному для реализации в системе И-НЕ:

J₂ = ,

K₂ = ,

J₁ = ,

K₁ = ,

J₀ = ,

K₀ = .

Теперь можно создать схему.

Таблица 6

№	Вход- ной сигнал	Исходное состояние (двоичное)			Новое состояние (двоичное или код Грея)			Q2		Q1		Q0		Примечание
	M	Q2	Q1	Q0	Q2н	Q1н	Q0н	J2	K2	J1	K1	J0	K0
0	0	0	0	0	0	0	1	0	-	0	-	1	-	Двоичный код – двоичный код
1	0	0	0	1	0	1	0	0	-	1	-	-	1
2	0	0	1	0	0	1	1	0	-	-	0	1	-
3	0	0	1	1	1	0	0	1	-	-	1	-	1
4	0	1	0	0	1	0	1	-	0	0	-	1	-
5	0	1	0	1	1	1	0	-	0	1	-	-	1
6	0	1	1	0	1	1	1	-	0	-	0	1	-
7	0	1	1	1	0	0	0	-	1	-	1	-	1
8	1	0	0	0	0	0	1	0	-	0	-	1	-	Двоичный код – код Грея
9	1	0	0	1	0	1	1	0	-	1	-	-	0
10	1	0	1	0	1	1	0	1	-	-	0	0	-
11	1	0	1	1	0	1	0	0	-	-	0	-	1
12	1	1	0	0	0	0	0	-	1	0	-	0	-
13	1	1	0	1	1	0	0	-	0	0	-	-	1
14	1	1	1	0	1	1	1	-	0	-	0	1	-
15	1	1	1	1	1	0	1	-	0	-	1	-	0

Таблица 7

	Q2	Q1	Q0
J	Q1Q0 MQ2 00 01 11 10 00 0 0 1 0 01 - - - - 11 - - - - 10 0 0 0 1	Q1Q0 MQ2 00 01 11 10 00 0 1 - - 01 0 1 - - 11 0 0 - - 10 0 1 - -	Q1Q0 MQ2 00 01 11 10 00 1 - - 1 01 1 - - 1 11 0 - - 1 10 1 - - 0
K	Q1Q0 MQ2 00 01 11 10 00 - - - - 01 0 0 1 0 11 1 0 0 0 10 - - - -	Q1Q0 MQ2 00 01 11 10 00 - - 1 0 01 - - 1 0 11 - - 1 0 10 - - 0 0	Q1Q0 MQ2 00 01 11 10 00 - 1 1 - 01 - 1 1 - 11 - 1 0 - 10 - 0 1 -

Задание 1:

1. – Изучить методику проектирования конечных автоматов.

2. – Реализовать схему конечного автомата примера 1 в EWB и проверить ее моделированием.

3. – Результаты показать преподавателю

Пример 2.

Спроектировать устройство управления светофором с такой последовательностью смены сигналов

• красный,

• красный + желтый,

• зеленый,

• желтый,

• красный и т.д.

Для решения этой задачи больше подходит автомат Мура, в котором цветными индикаторами могут управлять непосредственно выходы триггеров.

В качестве элементов памяти примем D – триггеры.

У светофора имеются индикаторы трех цветов, поэтому в качестве элементов памяти возьмем три D–триггера. Обозначим Q₀ – выход триггера, управляющего зеленым индикатором, Q₁ – выход триггера, управляющего желтым индикатором, Q₂ – выход триггера, управляющего красным индикатором. Примем, при Q_i = 1 индикатор светится, если Q_i = 0, то индикатор не светится.

Граф переходов проектируемого автомата можно представить так, как показано на рис. 3, где обозначено

100 – красный,

110 – красный + желтый,

001 – зеленый,

010 – желтый.

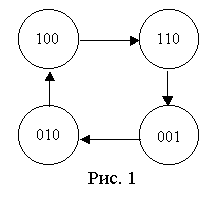
Рисунок 3 Граф рабочего цикла автомата

Составим совмещенную таблицу переходов и входов (табл. 8)

Таблица 8

Q2	Q1	Q0	D2	D1	D0
1	0	0	1	1	0
1	1	0	0	0	1
0	0	1	0	1	0
0	1	0	1	0	0

В левой части таблицы показаны возможные переходы автомата, в правой части – значения входных сигналов триггеров, вызывающих переход автомата в следующее состояние (при составлении таблицы учтено, что для D–триггера справедливо Q_н = D_ст).

Принимая D₂, D₁, D₀ функциями Q₂, Q₁, Q₀, составим карты Карно (табл. 9) и проведем минимизацию.

Таблица 9

D2						D1						D0
Q1Q0 Q2	00	01	11	10		Q1Q0 Q2	00	01	11	10		Q1Q0 Q2	00	01	11	10
0	x	0	x	1		0	x	1	x	0		0	x	0	x	0
1	1	x	x	0		1	1	x	x	0		1	0	x	x	1

Из карт Карно находим

D₀ = Q₁Q₂,

D₁ = ,

D₂ = .

Замечание. Для D₂ можно получить другое выражение, но цикл состояний 100, 110, 001, 010 сохранится.

Полученный автомат показан на рис. 4.

В данном автомате используются четыре состояния из восьми возможных.

Чтобы выяснить, как поведет себя автомат, если он окажется в одном из неиспользуемых состояний, по схеме составим полную таблицу переходов автомата (табл. 10).

В левой части таблицы приведены значения выходов триггеров, принимаемые за “старые” состояния (все возможные состояния), в правой части таблицы приведены новые значения выходов триггеров, равные значениям сигналов на входах D, если на выходах триггеров установлены старые состояния. (Сигналы на входах D определяются по схеме автомата.)

Р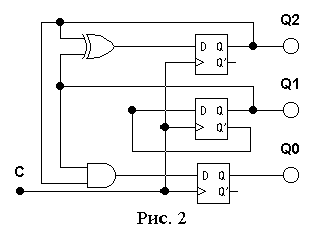 исунок 4

Таблица 10

Старые состояния			Новые состояния
Q2	Q1	Q0	Q2	Q1	Q0
0	0	0	0	1	0
0	0	1	0	1	0
0	1	0	1	0	0
0	1	1	1	0	0
1	0	0	1	1	0
1	0	1	1	1	0
1	1	0	0	0	1
1	1	1	0	0	1

На основе анализа полученной таблицы, можно составить граф переходов автомата, показанный на рис. 5. Из графа видно, что автомат переходит из любого неиспользуемого состояния в рабочий цикл за один шаг.

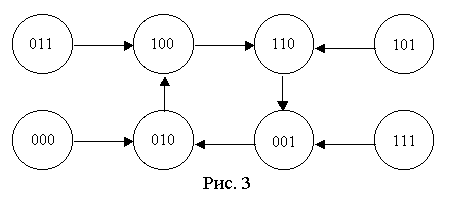
Рисунок 5