7. Подготовка к выполнению работы

1. Изучить описание лабораторной работы.

2. Спроектировать преобразователь кода «1 из N» в заданный десятичный код.

Указание: Сначала создать счетчик с Ксч = 10 в коде «1 из N» в виде простого кольца (см. рис. 15). Затем подключить к нему шифратор кода «1 из N» в заданный код (десятичный код выбирается по номеру исполнителя в журнале группы в п. Варианты заданий предыдущей работы «Счетчики»).

Напомним: Шифратор строится на элементах ИЛИ, количество которых равно числу разрядов образуемого кода, число входов у элементов ИЛИ равно числу 1 в колонках соответствующих разрядов в таблице истинности шифратора.

3. Создать счетчик Джонсона с коэффициентом счета Ксч = 10+M@7 и дешифратор к нему. Здесь М@7 остаток от деления номера исполнителя в журнале группы на 7. Схема счетчика должна иметь шину R для сброса счетчика в 0.

8. Порядок выполнения работы

1. В соответствии с заданием варианта создать в системе Electronics Workbench схему преобразователя кода «1 из N» в заданный десятичный код.

2. Проверить работу преобразователя в статическом и динамическом режимах.

3. Создать схему счетчика Джонсона с дешифратором, разработанных в п.7, проверить работу счетчика в статическом и динамическом режимах.

4. Показать преподавателю работу отлаженных схем с демонстрацией временных диаграмм на экране логического анализатора.

9. Отчет по работе

должен содержать

1. исходные данные варианта задания.

2. Полученные таблицы и формулы.

3. Схему преобразователя кода «1 из N» в заданный десятичный код и временные диаграммы его работы.

4. Схему счетчика Джонсона с дешифратором и временные диаграммы их работы.

Лабораторная работа № 7

КОНЕЧНЫЕ АВТОМАТЫ

Цель работы: овладеть методами синтеза конечных автоматов; приобрести практические навыки анализа работоспособности проектируемых схем.

1. Введение

Логические схемы с элементами памяти, относятся к классу автоматов. Наличие элементов памяти (ЭП) придает автомату А свойство иметь некоторое внутреннее состояние Q, определяемое совокупностью состояний всех элементов памяти. В зависимости от внутреннего состояния, автомат А различно реагирует на один и тот же вектор входных сигналов X. Воспринимая входные сигналы при определенном состоянии, автомат А переходит в новое состояние и вырабатывает вектор выходных переменных Z. Таким образом, для автомата А

Q_H = f(Q, X) и Z = φ (Q, X),

где Q_H и Q — состояния КА после и до подачи входных сигналов (индекс "н" от слова "новое").

Переходы автомата А из одного состояния в другое начинаются с некоторого исходного состояния Q₀, задание которого также является частью задания автомата. Следующее состояние зависит от Q₀ и поступивших входных сигналов X. В конечном счете, текущее состояние и выходы автомата зависят от начального состояния и всех векторов X, поступавших на автомат в предшествующих сменах входных сигналов. Таким образом, вся последовательность входных сигналов определяет последовательность состояний и выходных сигналов автомата А. Это объясняет название "последователъностные схемы", также применяемое для обозначения автоматов.

Из предыдущего следует, что для задания автомата А необходимо задать шестерку

А = {X, Z, Q, Q_H = f(Q, X), Z = φ (Q, X), Q₀}.

Здесь

X – входной алфавит – конечное множество возможных входных сигналов,

Z – выходной алфавит – конечное множество возможных выходных сигналов,

Q – конечное множество состояний автомата,

Q_H = f(Q, X) – функция переходов из каждого состояния в другие состояния,

Z = φ (Q, X) – функция формирования выходных сигналов,

Q₀ – начальное состояние автомата.

Автомат, заданный такой шестёркой, называется конечным (КА), так как X, Z, Q – конечные множества.

Структурно КА отличаются от комбинационных схем (КС) наличием обратных связей, вследствие чего в них проявляются свойства запоминания состояний. Автоматы с памятью в каноническом представлении разделяют на две части: память и комбинационную схему. На входы КС подаются входные сигналы и сигналы состояния КА. На ее выходе вырабатываются выходные сигналы Z и сигналы Y перевода КА в новое состояние.

Конечные автоматы делятся на асинхронные и синхронные. В асинхронных (рис. 1, а) роль элементов памяти играют элементы задержки, через которые сигналы состояния передаются на входы КС, чтобы совместно с новым набором входных переменных определить следующую пару значений Z и Q. Элементы КА переключаются здесь под непосредственным воздействием изменений информационных сигналов. Скорость распространения процесса переключений в цепях асинхронного автомата определяется собственными задержками элементов.

В синхронном КА (рис. 1, б) имеются специальные синхросигналы (тактирующие импульсы) С, которые разрешают элементам памяти прием данных только в определенные моменты времени. Элементами памяти служат синхронные триггеры. Процесс обработки информации упорядочивается во времени, и в течение одного такта возможно распространение процесса переключения только в строго определенных пределах тракта обработки информации.

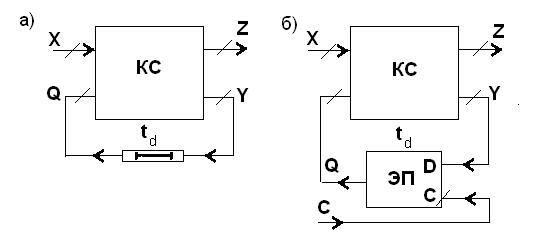
Рис. 1. Асинхронный (а) и синхронный (б) автоматы с памятью

Применение асинхронных автоматов затруднено сильным влиянием на их работу задержек сигналов в цепях КА, создающих статические и динамические риски, гонки элементов памяти (неодновременность срабатывания ЭП даже при одновременной подаче на них входных сигналов). В итоге характерным свойством асинхронного автомата является то, что при переходе из одного устойчивого состояния в другое он обычно проходит через промежуточные нестабильные состояния. Существуют методы борьбы с нежелательными последствиями рисков и гонок в асинхронных КА, но все же обеспечение предсказуемого поведения КА — сложная проблема. В более или менее сложных КА асинхронные схемы встречаются очень редко. Примером применения простейших асинхронных автоматов могут служить асинхронные RS-триггеры.

В синхронных автоматах каждое состояние устойчиво и переходные временные состояния не возникают. Идея борьбы с последствиями рисков и гонок в синхронных автоматах проста — прием информации в элементы памяти разрешается только после завершения в схеме переходных процессов. Это обеспечивается параметрами синхроимпульсов, задающих интервалы времени для завершения тех или иных процессов. В сравнении с асинхронными, синхронные КА значительно проще в проектировании.

В теории автоматов проводится их классификация по ряду признаков. Не вдаваясь в подробности, отметим, что в схемотехнике преобладают автоматы Мура, выходы которых являются функциями только состояния автомата. Для этого автомата

Q_H = f(Q, X) и Z = φ (Q).

Зависимость выходов Z и от состояния автомата и от вектора входных переменных свойственна автоматам Мили.

Некоторые функциональные узлы принадлежат к числу автономных автоматов, которые не имеют информационных входов, и под действием тактовых сигналов переходят из состояния в состояние по алгоритму, определяемому структурой автомата, к таким автоматам относятся, например, генераторы псевдослучайных чисел.