5. Регистры сдвига с обратными связями

На базе регистра сдвига можно построить схемы с различными функциональными возможностями. При введении обратных связей регистры сдвига могут работать как счетчики, генераторы кодов; дополнительная логика позволяет использовать их для преобразования кодов, умножения и деления двоичных чисел и т.д. Важно, что все эти функции реализуются с помощью дополнительной сравнительно простой комбинационной схемы.

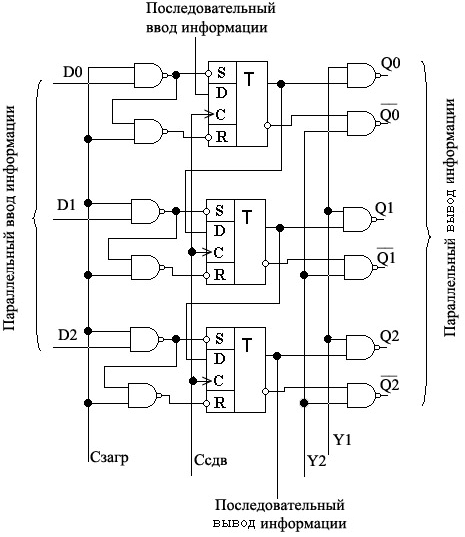
Рис. 13. Регистр сдвига с последовательным и

параллельным вводом и выводом информации

Наиболее простая схема с обратными связями получается, если выход последнего разряда регистра сдвига подключить к входу последовательного ввода данных. В этом случае непрерывная серия синхроимпульсов, подаваемых на шину сдвига, будет осуществлять режим циркуляции сдвигаемой информации. В режиме замкнутого в кольцо регистра сдвига по диаграмме выходных сигналов легко установить, правильно работает регистр или нет, а также определить динамические параметры регистра сдвига.

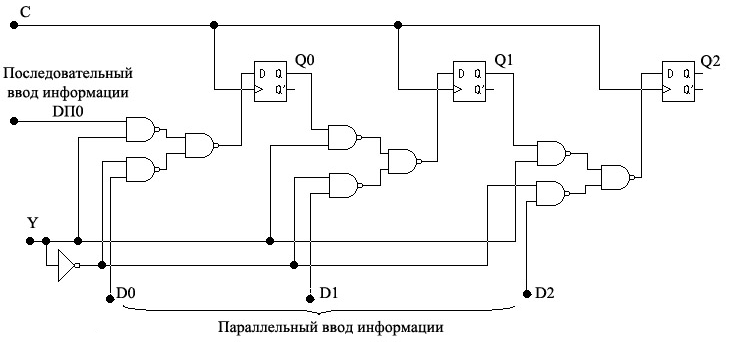Рис. 14. Регистр сдвига с последовательным и параллельным приемом

информации.

5.1. Простое кольцо

Кольцевой счетчик представляет собой регистр сдвига, у которого информационный D–вход триггера первого разряда соединен с выходом Q последнего разряда, образуя замкнутое кольцо (см. рис.15).

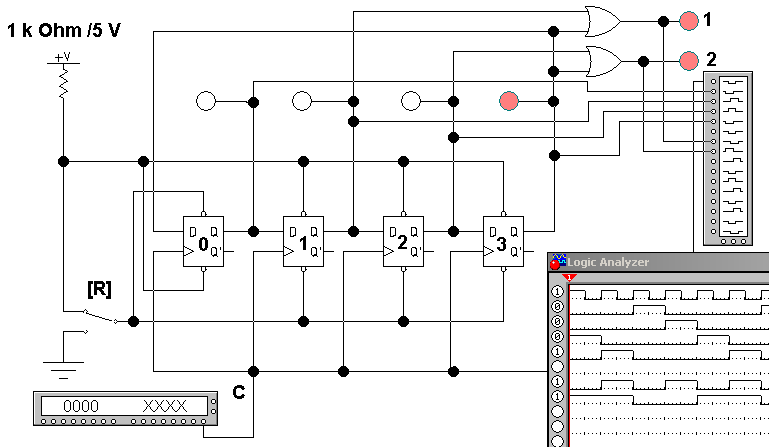
Рис. 15

На рис. 15 показаны схема и временные диаграммы работы четырехразрядного кольцевого счетчика на D–триггерах. В первый разряд регистра записывается единица (а в остальные разряды 0) сигналом от ключа R, затем эта единица тактовыми сигналами сдвига С перемещается из триггера в триггер. Коэффициент счета Ксч такого счетчика равен n, где n – число триггеров счетчика.

На этом же рисунке показан преобразователь (шифратор) унитарного кода «1 из 4» в двоичный код.

Кольцевые счетчики просты и обладает высоким быстродействием. К недостаткам кольцевых счетчиков следует отнести повышенное количество триггеров (например, для десятичного счетчика требуется 10 триггеров) и неспособность самовосстановления после сбоя состояния триггеров. Последний недостаток можно устранить введением корректирующей логической схемы.

5.2. Кольцо Мёбиуса – счетчик Джонсона

Если в регистре сдвига инверсный выход триггера последнего разряда соединить с информационным D–входом триггера первого разряда, то получим схему, которая называется счетчиком Джонсона и имеет коэффициент пересчета К_сч= 2n, где n – число триггеров счетчика. Схема десятичного счетчика Джонсона на D–триггерах приведена на рис. 16.

Р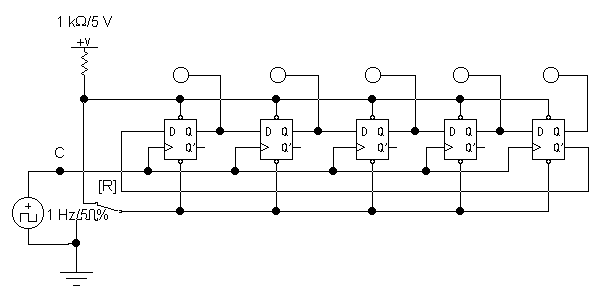 ис. 16

С игналом R триггеры счетчика устанавливаются в нулевое состояние. Входные сигналы счета подаются на входы С всех триггеров счетчика. Так как D₁ = = l, то первый входной сигнал счетчика С переключает триггер Т₁ в состояние 1, второй сигнал переключает триггеры T₁ и Т₂ в состояние 1 и т.д. После пятого входного импульса все триггеры установятся в состояние 1. Так как в этот момент = 0, то шестой входной сигнал установит триггер T₁ в состояние 0. Седьмой входной сигнал установит триггеры T₁ и Т₂ в состояние 0 и т.д. Десятый входной сигнал возвращает триггеры счетчика в начальное нулевое состояние. Таким образом, при счете происходит заполнение триггеров счетчика единицами, начиная с T₁, а затем после того, как все триггеры оказались в состоянии 1, происходит последовательная установка триггеров в состояние 0, начиная с триггера T₁.

Если кодирование десятичных цифр выполняется в соответствии с табл. 1, то дешифрирование десятичных цифр получается путем реализации простых функций двухвходовыми элементами И:

, ,

, ,

, ,

, ,

, ,

что следует из карт Карно для этих функций, приведенных в табл. 2. На карте Карно знаком х отмечены значения выходной функции дешифратора на неиспользуемых наборах аргументов , а цифрами 0, 1, 2,…, 9 – клетки, которым соответствуют конституенты единицы, отображающие эти десятичные цифры.

В качестве примера в табл. 2 показаны объединения клеток при получении функций, соответствующих цифрам 1 (овалы) и 2 (прямоугольник).

Счетчик Джонсона имеет высокое быстродействие. Задержка распространения t_{зд.р.сч.} сигнала от входа счетных импульсов до выхода счетчика равна задержке распространения t_{зд.р.С–Q} сигнала от входа С до выхода Q одного триггера, т.е.

Счетчик Джонсона просто перестраивается на меньшие модули счета. Для этого вход D₁ триггера первого разряда соединяется не с выходом , а с другими инверсными выходами. Вид функции обратной связи, реализуемой на входе D₁ для различных модулей счета, приведен в табл. 3.

Таблица 1

Десятичная цифра.	Q1	Q2	Q3	Q4	Q5
0	0	0	0	0	0
1	1	0	0	0	0
2	1	1	0	0	0
3	1	1	1	0	0
4	1	1	1	1	0
5	1	1	1	1	1
6	0	1	1	1	1
7	0	0	1	1	1
8	0	0	0	1	1
9	0	0	0	0	1

Таблица 2

Q3Q2Q1 Q5Q4	000	001	011	010	110	111	101	100
00	0	1	2	х	х	3	х	х
01	х	х	х	х	х	4	х	х
11	8	х	х	х	6	5	х	7
10	9	х	х	х	х	х	х	х

Таблица 3

Значение модуля	Функция обратной связи
2
3
4
5
6
7
8
9
10

Таблица переходов и функции возбуждения D₁ триггера Т₁ (табл. 4) и карта Карно функции D₁ (табл. 5) иллюстрируют построение счетчика Джонсона с модулем счета 9.

На карте Карно (табл. 5) знаком х отмечены произвольные значения функции на неиспользуемых наборах. Склеивание конституент единицы, выделенных на карте Карно полужирным шрифтом и подчеркиванием, дает функцию возбуждения . (Если регистр построен на JK–триггерах, то .)