2.1. Счетчик на d–триггерах

Таблица переходов одного разряда двоично–десятичного счетчика в коде 2421 не зависит от типа триггера и может быть представлена колонками 1–8 табл. 8, идентичными колонкам 1–8 табл.5.

Для составления функций возбуждения каждого триггера десятичного разряда счетчика на D–триггерах воспользуемся таблицей входов D–триггера (табл. 1).

В соответствии с этой таблицей в первой строке табл. 8 в столбцах 9, 10, 11 необходимо записать 0, а в столбце 12 поставить 1 (у D–триггера Q_н = D_ст).

Аналогично заполняются остальные строки табл. 8.

Минимизацию функций возбуждения триггеров проведем с помощью карт Карно (табл. 9). В результате получаем следующие функции возбуждения

D₁ = , D₂ = ,

D₃ = , D₄ = .

Теперь можно создать схему одного разряда десятичного счетчика на D–триггерах.

3. Организация переноса

В каждом десятичном разряде при переходе из состояния 9 в состояние 0 (в рассматриваемом примере из состояния S₁₅ в состояние S₀) необходимо вырабатывать сигнал переноса в следующий разряд. В простейшем случае (если это возможно) в качестве сигнала переноса можно использовать выходной сигнал старшего двоичного разряда (Q₄). Для уменьшения времени задержки переноса каждый десятичный разряд можно рассматривать как группу из четырех разрядов и схему, формирующую сигнал переноса для счетчиков на JK–триггерах, изменяющих свое состояние по срезу счетного импульса, можно построить, используя выражение

Сout_i = Cout_{i –1}K_ф,

где Cout_{i –1} – сигнал переноса из предыдущего десятичного разряда; K_ф – конституента единицы, соответствующая десятичной цифре 9.

(Для данного примера 9 соответствует 15, поэтому K_ф = Q₄Q₃Q₂Q₁. См. табл. 4 и табл. 5).

Таблица 8
Таблица функций возбуждения триггеров счетчика
Десятичная цифра	Номер набора	Выходы триггеров								Функции возбуждения D–триггеров
		Старые значения				Новые значения				Т4	Т3	Т2	Т1
		Q4	Q3	Q2	Q1	Q4	Q3	Q2	Q1	D4	D3	D2	D1
		1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	0	0	0	0	0	0	1	0	0	0	1
1	1	0	0	0	1	0	0	1	0	0	0	1	0
2	2	0	0	1	0	0	0	1	1	0	0	1	1
3	3	0	0	1	1	0	1	0	0	0	1	0	0
4	4	0	1	0	0	1	0	1	1	1	0	1	1
5	11	1	0	1	1	1	1	0	0	1	1	0	0
6	12	1	1	0	0	1	1	0	1	1	1	0	1
7	13	1	1	0	1	1	1	1	0	1	1	1	0
8	14	1	1	1	0	1	1	1	1	1	1	1	1
9	15	1	1	1	1	0	0	0	0	0	0	0	0

Таблица 9

Счетчик на D–триггерах
D1							D2
Q2Q1 Q4Q3	00	01	11	10			Q2Q1 Q4Q3	00	01	11	10
00	1	0	0	1			00	0	1	0	1
01	1	х	х	х			01	1	х	х	х
11	1	0	0	1			11	0	1	0	1
10	х	х	0	х			10	х	х	0	х
D3							D4
Q2Q1 Q4Q3	00	01	11	10			Q2Q1 Q4Q3	00	01	11	10
00	0	0	1	0			00	0	0	0	0
01	0	х	х	х			01	1	х	х	х
11	1	1	0	1			11	1	1	0	1
10	х	х	1	х			10	х	х	1	х

Конституента единицы не всегда отвечает минимальному выражению, необходимому для образования сигнала переноса. В десятичных счетчиках всегда имеются запрещенные состояния, учет которых позволяет упростить выражение для сигнала переноса. Для этого необходимо занести на карту Карно запрещенные состояния (х) и конституенту единицы (1) того набора, который соответствует десятичной цифре 9 в данном двоично–десятичном коде. Остальные клетки диаграммы заполняются нулями (табл. 10). Например, для рассматриваемого случая, объединив клетки, выделенные полужирным шрифтом, получим минимальное выражение для сигнала переноса. Таким образом, получаем

Сout_i = Cout_{i –1}Q₃Q₂Q₁

и, следовательно, сигнал переноса можно сформировать с помощью элемента И, на входы которого подаются сигналы Cout_{i –1}, Q₃, Q₂, Q₁.

Таблица 10

Карта Карно для переноса
Q2Q1 Q4Q3	00	01	11	10
00	0	0	0	0
01	0	х	х	х
11	0	0	1	0
10	х	х	0	х

Для счетчика на D–триггерах рассуждения относительно сигнала переноса в следующий разряд похожи на предыдущие, но эти триггеры срабатывают по фронту счетного сигнала, а потому в простейшем случае переносом может быть сигнал, снимаемый с инверсного выхода старшего разряда декады, а групповой перенос, казалось бы, можно сформировать на основе выражения

Сout_i = Cout_{i –1}K_н,

где K_н – конституента единицы, соответствующая начальной десятичной цифре кода. (Для данного примера начальная цифра кода равна 0, см. табл. 4 и табл. 5, поэтому K_н = ).

Однако при такой реализации переноса возможно появление ложных сигналов из–за риска сбоя (см. рис. 4,а).

На рис. 4,а приведена схема переноса из группы, состоящей из одного D–триггера. Здесь комбинационная схема представлена двумя элементами И, на выходах которых реализуются уравнения:

Задержка переключения триггера в данном случае приводит к появлению статических рисков сбоя в обоих случаях при переходе с набора 01 на набор 10. Устранить эти сбои можно, выполнив комбинационную схему на элементах ИЛИ (рис. 4,б).

Из временных диаграмм видно, что в данной схеме ложные сигналы из-за рисков сбоя не появляются. Выходные сигналы С1 и С2 при необходимости можно изменить инвертированием.

В счетчике на JK-триггерах, срабатывающих по срезу импульса на тактовом входе, риска сбоя нет (рис. 4,в).

Таким образом, перенос в счетчиках на D–триггерах лучше сделать на элементе ИЛИ, реализующем выражение

Cout_i = Cout_{i –1} ,

полученное как КНФ по карте Карно.

Р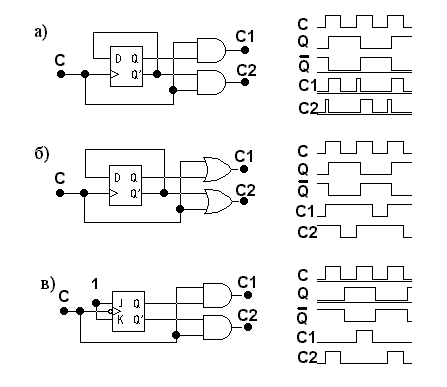 ис. 4

Таблица 11

Карта Карно для переноса
Q2Q1 Q4Q3	00	01	11	10
00	1	0	0	0
01	0	х	х	х
11	0	0	0	0
10	х	х	0	х