2. Пример проектирования двухступенчатого триггера

Пусть задана таблица переходов триггера табл. 1 (Вариант 30).

Таблица 1

Таблица переходов

№	x1(t)	x2(t)	Q(t+1)
30	0 0 1 1	0 1 0 1	Q(t) 0 1

Составим таблицу истинности для функций возбуждения и триггера первой ступени (см. рис. 1). Аргументами для данных функций являются выход триггера Q, входы x₁, x₂ и C, т.е. существуют 2⁴ = 16 наборов входных переменных, на которых надо определить значения функций (переменная представлена переменной Q). Для пояснения выбора значений и укажем в таблице также новые значения (в момент времени t+1) выхода триггера первой ступени Q1.

При определении значений функций и в таблице истинности функций возбуждения нам потребуется таблица входов одноступенчатого –триггера.

По таблице входов можно определить, какие сигналы надо подать на входы для перевода триггера из одного состояния в другое. Таблица входов одноступенчатого –триггера составляется по его таблице переходов (табл. 2).

Замечание:

В таблицах переходов (табл. 2) символом “*” обозначено состояние при запрещенном входном наборе.

Представим таблицу переходов –триггера (табл. 2) в развернутом виде (табл. 3).

Просматривая эту таблицу, замечаем, что для перевода триггера из состояния 0 в состояние 0 можно использовать либо набор = 01, либо = 11, т.е. значение сигнала на входе безразлично какое (0 или 1). Обозначим такой сигнал символом -. Для перевода триггера из состояния 0 в состояние 1 необходимо подать набор = 10. Для перевода триггера из состояния 1 в состояние 0 необходимо подать набор = 01. Для перевода триггера из состояния 1 в состояние 1 можно подать на входы набор = 10 или набор = 11, т.е. на вход можно подать или 0, или 1. Этот сигнал обозначили через -.

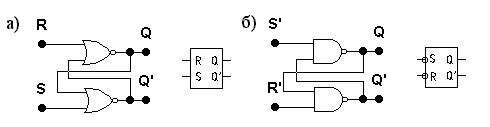
Рис. 2. Запоминающая ячейка (асинхронный RS–триггер)

а) RS–триггер с прямыми входами на элементах ИЛИ–НЕ

и его условное графическое обозначение;

б) –триггер с инверсными входами на элементах И–НЕ

и его условное графическое обозначение

(в EWB такого триггера в виде условного обозначения нет)

Таблица 2

–триггер
t		t+1
R’	S’	Q
0	0	*
0	1	0
1	0	1
1	1	Qt

Таблица 3

Qt	R’	S’	Qt+1
*	0*	0*	*
0	0	1	0
0	1	0	1
0	1	1	0
*	0*	0*	*
1	0	1	0
1	1	0	1
1	1	1	1

* – набор 00 для –триггера запрещен.

Оформив все эти рассуждения в виде таблицы, получаем таблицу входов –триггера (табл. 4).

При формировании таблицы истинности функций и (табл. 5) отдельно рассмотрим верхнюю ее половину (при С = 0) и нижнюю (при С = 1). При С = 0 функции и должны иметь такие значения, которые не меняют состояния триггера первой ступени (состояние первой ступени и второй ступени при С = 0 одинаково, т.е. значение выхода Q равно значению выхода Q1 (см. рис. 1)).

Рассмотрим первую строчку табл. 5. Так как С = 0, то значения функций и не должны изменять значение выхода Q1 = Q = 0. Это возможно, если функция будет равна 1, a равна - (см. таблицу входов табл. 4). Напомним – символ - означает, что можно придать любое значение: "0" или "1", что эквивалентно неопределенному значению.

Таблица 4

Qt	Q1t+1	R’	S’
0	0	-	1
0	1	1	0
1	0	0	1
1	1	1	-

Таблица 5

Таблица истинности функций возбуждения

запоминающей ячейки x₁x₂–триггера

C	x1	x2	Q	Q1t+1
0	0	0	0	0	-	1
0	0	0	1	1	1	-
0	0	1	0	0	-	1
0	0	1	1	1	1	-
0	1	0	0	0	-	1
0	1	0	1	1	1	-
0	1	1	0	0	-	1
0	1	1	1	1	1	-
1	0	0	0	0	-	1
1	0	0	1	1	1	-
1	0	1	0	0	-	1
1	0	1	1	0	0	1
1	1	0	0	1	1	0
1	1	0	1	1	1	-
1	1	1	0	1	1	0
1	1	1	1	0	0	1

Рассмотрим вторую строчку. Здесь Q1 = Q = 1. Чтобы состояние запоминающей ячейки не изменилось, значение функции должно быть равно "1", а может принимать произвольное значение, т.е. = - на данном наборе. Рассуждая аналогичным образом, заполним всю первую половину таблицы. Поскольку при формировании этой части таблицы не рассматривались значения сигналов x₁ и x₂, то такое содержание таблицы неизменно для любого триггера подобной структуры.

Для заполнения нижней части табл. 5, кроме таблицы входов (табл. 4), понадобится также таблица переходов синтезируемого триггера (табл. 1 - вариант 30).

Рассмотрим первую строчку второй половины табл. 5. Здесь значения входных переменных следующие: C = 1, Q = 0, x₁= 0, x₂ = 0. Теперь обратимся к таблице переходов x₁x₂ –триггера. При x₁ = x₂ = 0 триггер не изменяет своего состояния, следовательно, Q1 = Q = 0 и = 1, = - на данном наборе, так как триггер должен остаться в состоянии 0 (символ - означает любое значение: 0 или 1). Вторая строчка этой половины таблицы отличается от первой только значением Q = 1. Следовательно, для этого набора Q1 = Q = 1 и = -, = 1.

Рассмотрим комбинацию входных переменных С = 1, x₁ = 0, x₂ = 1, Q = 1 (в таблице выделены полужирным шрифтом).

В соответствии с таблицей переходов при x₁ = 0, x₂ = 1 триггер должен изменить свое состояние с 1 на 0. Чтобы триггер так изменил свое состояние, значение функции должно быть равно 1, a – 0. Проводя подобные рассуждения, заполняем всю таблицу истинности.

После заполнения таблицы истинности находим минимальные выражения для функций и с помощью карт Карно (табл. 7 и табл. 8). В результате минимизации получим следующие выражения для функций возбуждения:

Таблица 7 Таблица 8

Карта S’						Карта R’
x2Q Cx1	00	01	11	10		x2Q Cx1	00	01	11	10
00	1	-	-	1		00	-	1	1	-
01	1	-	-	1		01	-	1	1	-
11	0	-	1	0		11	1	1	0	1
10	1	-	1	1		10	-	1	0	-

На рис. 3 приведена схема спроектированного триггера. В отличие от схемы, изображенной на рис. 1, здесь схема дополнена асинхронными входами предварительной установки триггера в состояние "0" или "1". Буквой (S’) обозначают асинхронный вход для установки триггера в состояние "1", а буквой (R’) – асинхронный вход для установки триггера в состояние "0". Сигналы, поступающие на эти входы, пользуются приоритетом, т.е. независимо от сигналов на других входах триггера они сразу (по переднему фронту) устанавливают триггер в определенное состояние. Синхронный триггер по установочным входам реализует таблицу переходов асинхронного –триггера. Наличие у синхронного триггера асинхронных входов иногда указывают в его обозначении, записывая после сокращенного обозначения информационных входов обозначения асинхронных входов, например, JK –триггер.

Работу триггера по установочным входам можно было учесть в процессе проектирования, но это увеличило бы размерность задачи. Поскольку организация входов предварительной установки практически неизменна для любого синхронного двухступенчатого триггера, то просто введем ее в схему триггера.

Р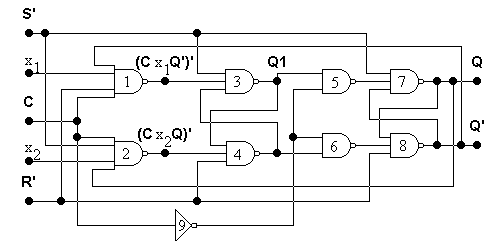 ис. 3. Синхронный двухступенчатый x₁x₂–триггер

с асинхронными входами и

Из анализа работы двухступенчатого триггера данного типа видно, что при С = 0 сигналы на информационных входах не влияют на состояние триггера, а триггер второй ступени копирует состояние триггера первой ступени, так как открыты элементы связи, разделяющие оба триггера. Если теперь специальным сигналом изменить состояние триггера первой ступени, то, очевидно, изменит свое состояние и триггер второй ступени (скопирует новое состояние триггера первой ступени). Время, через которое на выходах двухступенчатого триггера установится новое состояние, будет определяться задержкой, вносимой четырьмя последовательно включенными логическими элементами. Для уменьшения времени переключения триггера сигнал предварительной установки в заданное состояние подается одновременно на триггеры первой и второй ступени. Сигнал подается на элементы 3 и 7, а сигнал подается на элементы 4, 8 (см. рис. 3). При этом новое состояние триггера установится через время, равное времени задержки двух элементов (время фиксации нового состояния –триггером), а не четырех.

При С = 1 состояние информационных входов непосредственно воздействует на состояние триггера первой ступени двухступенчатого триггера. Поэтому при подаче установочного сигнала на входах этого триггера может появиться запрещенная комбинация сигналов. Чтобы исключить появление запрещенной комбинации сигналов, установочные сигналы подают и на схему управления первой ступени (сигнал поступает на элемент 1, а сигнал поступает на элемент 2, см. рис. 3).

В данном разделе в качестве примера рассмотрено построение двухступенчатого триггера на элементарных запоминающих ячейках типа –триггеров (на элементах И-НЕ), но в Схемотехнике имеется и другой тип элементарных запоминающих ячеек – RS–триггеры (на элементах ИЛИ-НЕ) (см. рис. 2 и табл. 9) и, поскольку в двухступенчатый триггер входит две ячейки, то возможно построение четырех вариантов двухступенчатых триггеров на однотипных и разнотипных элементарных запоминающих ячейках. Кроме того, существует структурная схема двухступенчатого триггера с запрещающими связями, на базе которой можно построить еще четыре варианта триггеров (все эти варианты представлены выше в п. 1.3. JK–триггер).

Таблица 9

RS–триггер
t		t+1
R	S	Q
0	0	Qt
0	1	1
1	0	0
1	1	*