1. Создание схем 123

1.1. Технология построения схем 123

1.2. Исследование схем 128

1.3. Контрольные вопросы 129

2. Технология составления отчета 129

2.1. Требования к отчету 129

2.2. Вывод результатов на принтер 130

Лабораторная работа №1 логические функции и схемы

Цель работы: овладеть методами синтеза и исследования простейших комбинационных логических схем.

1. Комбинационные схемы

Комбинационной схемой называется логическая схема, реализующая однозначное соответствие между значениями входных и выходных сигналов. Это схема без обратных связей, поэтому ее работа не зависит от времени (схема без памяти). Для реализации комбинационных схем используются логические элементы и функциональные узлы, выпускаемые в виде интегральных схем.

К функциональным узлам относятся схемы дешифраторов, шифраторов, мультиплексоров, демультиплексоров, сумматоров и другие.

2. Аксиомы алгебры логики

Переменные, рассматриваемые в алгебре логики, могут принимать только два значения: 0 или 1. В алгебре логики определены отношение эквивалентности (обозначается знаком =), операция логического сложения (дизъюнкции), обозначаемая знаком , логического умножения (конъюнкции), обозначаемая знаками &, или точкой (иногда конъюнкция никак не обозначается, например, A&B = A B = A∙B = AB), и отрицания (инверсии), обозначаемая надчеркиванием или апострофом ‘.

В алгебре логики задаются следующие аксиомы:

x = 1, если x 0; x = 0, если x 1;

0&0 = 0; 1 1 = 1

1&1 = 1; 0 0 =0;

1&0 = 0&1 = 0; 0 1 = 1 0 = 1;

1; = 0.

3. Тождества алгебры логики

Для преобразования и упрощения логических выражений используются различные логические тождества, например:

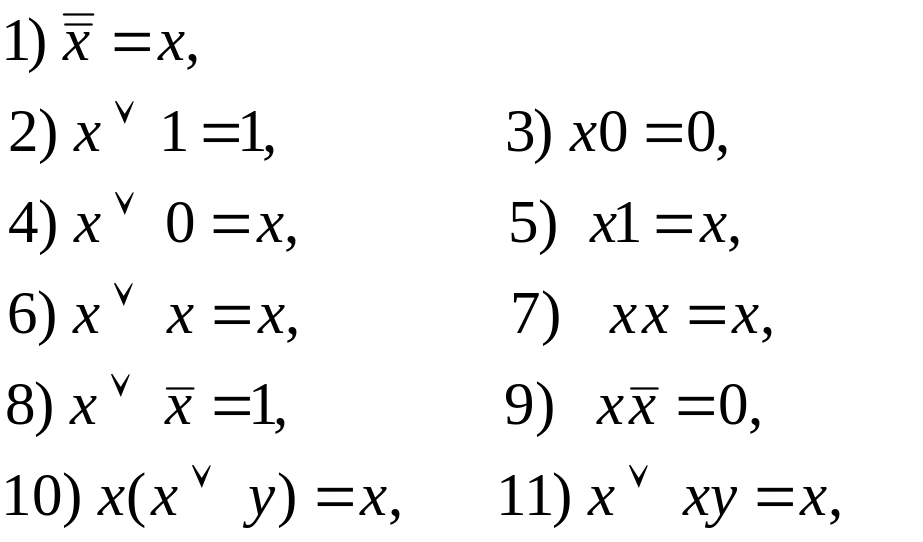
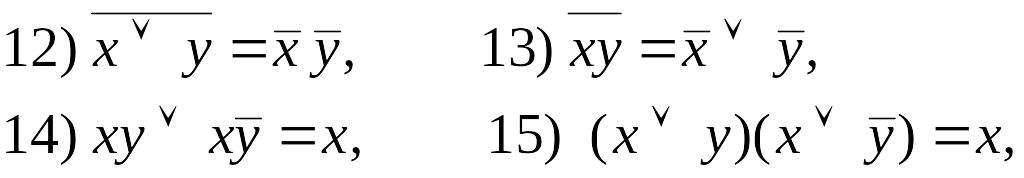
Соотношения 12) и 13) носят название формул де-Моргана. Эти и другие тождества могут быть доказаны с помощью таблиц истинности (см. ниже).

4. Логические функции

Любое логическое выражение, составленное из n переменных с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию n переменных. Такую функцию называют логической. В соответствии с аксиомами алгебры логики функция может принимать в зависимости от значения переменных значение 0 или 1. Функция n логических переменных может быть определена для 2ⁿ значений переменных, соответствующих всем возможным комбинациям n-разрядных двоичных чисел. Основной практический интерес представляют следующие функции двух переменных х и у:

f₁(x,y) = x & y = x y = x – логическое умножение (конъюнкция);

f₂(x,y) = x y – логическое сложение (дизъюнкция);

f₃(x,y) = = – штрих Шеффера;

f₄(x,y) = = – стрелка Пирса;

f₅(x,y) = x y = – сложение по модулю 2;

f₆(x,y) = – равнозначность.

5. Таблица истинности

Так как область определения любой логической функции n переменных конечна (2ⁿ значений), то она может быть задана таблицей значений f(i), которые функция принимает на наборах переменных с номерами i, где i = 0,…, 2ⁿ-1. Такие таблицы называют таблицами истинности. В табл. 1 представлены таблицы истинности, задающие перечисленные выше функции.

В таблице номер строки (№) есть десятичная запись соответствующего двоичного кода набора переменных.