5. Подготовка к выполнению работы

1. Изучить описание лабораторной работы.

2. Создать схему мультиплексора 4–1 с одним входом управления. Активный уровень выхода мультиплексора логическая единица.

3. Создать схему, реализующую на мультиплексоре заданную логическую функцию трех переменных.

4. Создать схему, реализующую на мультиплексоре заданную частично определенную логическую функцию четырех переменных.

5. Создать схему, реализующую на мультиплексорах заданную систему логических функций четырех переменных.

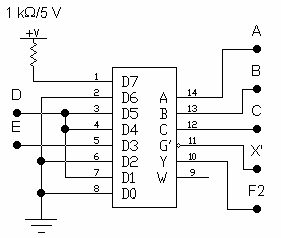
Рис. 3.10. Реализация функции F2 на мультиплексоре 8-1

6. Порядок выполнения работы

1. Используя Electronics Workbench, синтезировать мультиплексор 4–1 с одним входом управления. Активный уровень выхода мультиплексора логическая единица. Провести моделирование и получить временные диаграммы. Оценить время задержки схемы, используя параметры элементов.

2. Из схемы п.1 создать субблок мультиплексора 4–1 с одним входом управления. Используя полученный субблок, создать мультиплексоры 8–1 и 16–1. Проверить их работоспособность моделированием.

3. Реализовать на мультиплексорах логические функции, исследованные в лабораторной работе №1. Провести моделирование и получить временные диаграммы. Оценить время задержки схем.

4. Показать преподавателю работу созданных схем с демонстрацией на экране логического анализатора временных диаграмм.

7. Отчет по работе

Отчет по работе должен содержать

1. исходные данные варианта задания.

2. Рисунки исследованных схем и их временные диаграммы.

3. оценку быстродействия полученных схем.

8. Контрольные вопросы и задания

1. В чем состоит принцип работы мультиплексора?

2. Запишите аналитическое выражение, описывающее работу мультиплексора MS 2 ‑1 (4 ‑1) с прямым (инверсным) входом разрешения.

3. Как изменятся уравнение и схема мультиплексора MS 4–1, если пассивное состояние выхода должно быть 1?

4. В чем различие мультиплексоров, показанных на рис. 3.3,б и 3.4? Попробуйте создать логическую схему мультиплексора рис. 3.4.

5. Почему управляющие сигналы в схемах мультиплексоров рис. 3.2 подаются через инверторы?

6. Каким соотношением связаны число информационных и число управляющих входов? А число входов и выходов?

7. Постройте схему простейшего мультиплексора MS 2 ‑1 на базе элемента И‑ИЛИ‑НЕ.

8. Постройте схему мультиплексора MS 4 ‑1 (8 ‑1) на заданных элементах: а) И, ИЛИ, НЕ; б) И‑НЕ; в) ИЛИ‑НЕ.

9. Реализуйте с помощью мультиплексора произвольную, заданную преподавателем логическую функцию.

10. На базе готовых мультиплексоров MS 2 ‑1 (4 ‑1) постройте один мультиплексор MS 4 ‑1 (16 ‑1).

11. Логические функции скольких переменных можно реализовать на мультиплексоре MS 4 ‑1 (8 ‑1, 16 ‑1) с одним входом разрешения?

Лабораторная работа № 4

триггеры

Цель работы: овладеть методами синтеза триггерных структур; приобрести практические навыки анализа работоспособности проектируемых схем.

1. Теоретические основы

1.1. Введение

У изученных в предыдущих лабораторных работах комбинационных схем состояние выхода Y в любой момент времени определяется только текущим состоянием входа X, т.е. Y = F(X). В отличие от них состояние выхода последовательностной схемы (цифрового автомата) зависит еще и от внутреннего состояния схемы Q: Y = F(Х, Q). Другими словами, цифровой автомат “помнит” свое прошлое состояние. Это свойство обеспечивается наличием в схеме обратных связей.

Основой последовательностных схем являются триггеры. Триггер – простейшая логическая схема последовательностного типа. Триггер имеет два устойчивых состояния 1 и 0, поэтому его иногда называют бистабильной схемой. В каком из этих состояний окажется триггер, зависит от сигналов на входах триггера и от его предыдущего состояния. Можно сказать, что триггер является элементарной однобитовой (0,1) ячейкой памяти – он помнит свое предыдущее состояние.

Триггер может иметь один или два выхода (прямой Q и инверсный ), установочные, информационные и управляющие входы. Сигналы, поданные на установочные входы, переводят триггер в то или иное состояние независимо от того, в каком состоянии триггер находился в предыдущий момент времени, и независимо от сигналов на других входах. Эти входы называют асинхронными. Сигналы на входах управления разрешают прием данных, поступающих на информационные входы.

Тип триггера определяется алгоритмом его работы. Наиболее распространенными являются RS–, JK–, D– и Т–триггеры.

1.2. RS–триггер

RS–триггер простейший автомат с памятью, который может находиться в одном из двух состояний 0 или 1.

RS–триггер имеет два входа: установки в 1 – S (set) и сброса в 0 – R (reset), и два выхода: прямой Q и инверсный .

При подаче на вход S сигнала с активным логическим уровнем (низким или высоким – у разных триггеров разные активные уровни входных сигналов) триггер устанавливается в единичное состояние (Q = 1, = 0). при подаче сигнала с активным логическим уровнем на вход R триггер устанавливается в нулевое состояние (Q = 0, = 1). Если подать на оба входа сигнал с пассивным уровнем, то триггер будет сохранять предыдущее состояние. Каждое состояние устойчиво и поддерживается за счет действия обратных связей.

Для триггеров этого типа недопустима одновременная подача активного уровня на оба входа установки, так как триггер по определению не может одновременно быть установлен в ноль и единицу. На практике подача активного уровня на оба установочные входы приводит к тому, что состояние, в которое переходит триггер, не может быть сохранено, и невозможно определить, в каком состоянии будет находиться триггер при последующей подаче на установочные входы сигналов пассивного уровня. Поэтому подача сигналов активного уровня на оба входа RS–триггера запрещена!

RS–триггер является основным узлом для построения последовательностных схем. Название «последовательностные» означает, что состояние выхода зависит от того, в какой последовательности на входы подаются входные наборы, и каково было предшествующее внутреннее состояние. Так, если на входах RS–триггера вначале установить комбинацию R = 0, S = 1 (сокращенная запись 01), а потом перейти к R = 0, S = 0 (00), то состояние выхода будет Q = 1. Если же вначале установить комбинацию 10, а потом перейти к 00, то состояние выхода будет другим – Q = 0, несмотря на одинаковые конечные комбинации сигналов на входах. Таким образом, при одном и том же входном наборе 00 триггер может находиться в разных состояниях.

Условия переходов триггеров из одного состояния в другое (алгоритм работы) можно описать табличным, аналитическим или графическим способами. Табличное описание работы RS–триггера, представленного в виде “черного ящика” (рис. 4.1), показано в табл. 4.1 (активный уровень высокий). Эта таблица называется таблицей переходов RS–триггера.

Входными сигналами в таблице считаются сигналы на внешних входах R, S и сигнал обратной связи Q_ст, имитирующий предыдущее состояние триггера. Выходной сигнал, обозначенный Q_нов, имитирует новое состояние, в которое триггер переходит из состояния Q_ст при подаче на внешние входы соответствующего набора. Символом * обозначено неопределенное состояние, которое возникает при подаче на оба внешних входа сигналов с активным уровнем.

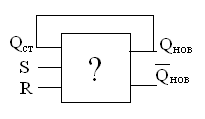
Рис. 4.1

Довольно часто вместо полной таблицы переходов используют сокращенную таблицу переходов RS–триггера (см. таб. 4.2), в которой показано, что при подаче на входы сигналов с пассивным уровнем старое состояние триггера сохраняется. При подаче на оба входа сигналов с активным уровнем возникает неопределенное состояние *. Входной набор R = 0, S = 1 устанавливает триггер в единичное состояние, а набор R = 1, S = 0 в нулевое состояние.

Таблица 4.1

Qст	R	S	Qнов
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	*
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	*

таблица 4.2

R	S	Qнов
0	0	Qст
0	1	1
1	0	0
1	1	*

Таблица 4.1 позволяет считать Q_нов частично определенной функцией, что дает возможность получить несколько вариантов схем триггера.

Таблица 4.3

Qст\RS	00	01	11	10
0	0	1	1*	0
1	1	1	1*	0

Таблица 4.4

Qст\RS	00	01	11	10
0	0	1	0*	0
1	1	1	0*	0

Таблица 4.5

Qст\RS	00	01	11	10
0	0	1	0*	0
1	1	1	1*	0

Таблица 4.6

Qст\RS	00	01	11	10
0	0	1	1*	0
1	1	1	0*	0

В табл. 4.3 – 4.6 приведены карты Карно с различными вариантами доопределения функции Q_нов= f(R, S, Q_ст). Доопределяемые клетки таблицы помечены символом *. По этим картам Карно находим следующие четыре минимальные формы

1. .

2. .

3. .

4.

Попытаемся реализовать все четыре формы.

Первая форма наиболее просто реализуется на элементах И–НЕ (рис. 4.2)

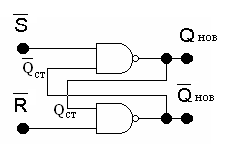
Рис. 4.2

Вторую форму удобно реализовать на элементах ИЛИ–НЕ (рис. 4.3)

.

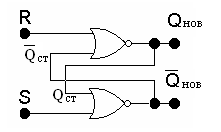
Рис. 4.3

Третья форма содержит три терма и ее реализация сложнее первых двух. Реализуем ее на элементах И–НЕ

Схема на рис. 4.4 носит название Е–триггер. Характерная особенность этого триггера – у него нет запрещенных входных наборов, и при 00 и при 11 триггер сохраняет старое состояние (применяется весьма редко).

Четвертую форму удобно было бы реализовать в виде инверсии Q_нов

.

Это позволяет использовать эквивалент элемента И–ИЛИ–НЕ и два инвертора рис. 4.5.

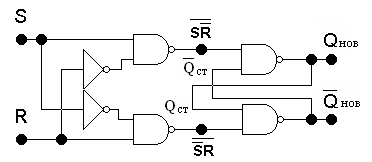
Рис. 4.4

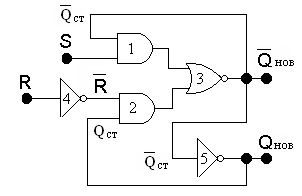
Рис. 4.5

Однако полученная схема оказывается неустойчивой при входном наборе RS = 11. Действительно, если , то сигнал S = 1 проходит через элемент И1 на элемент ИЛИ–НЕ3 и становится нулем, в результате на обоих входах элемента ИЛИ–НЕ3 нули, следовательно, опять и т.д. (См. временную диаграмму рис. 4.6.)

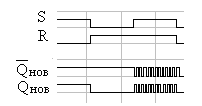
Рис. 4.6

Из-за неустойчивости эта схема в таком виде не применяется, а после существенной доработки превращается в JK–триггер (см. ниже).

Описание работы RS–триггера можно также представить графом (рис. 4.7).

Граф на рис. 4.7,а показывает, что схема, которая находилась в состоянии Q = 0, сохраняет это состояние как при воздействии входного набора R = 0, S = 0, так и при воздействии R = 1, S = 0. Если же на входы схемы, находящейся в состоянии Q = 0, подать набор R = 0, S = 1, то она переходит в состояние Q = 1 и сохраняет его при входных наборах R = 0, S = 1, либо R = 0, S = 0.

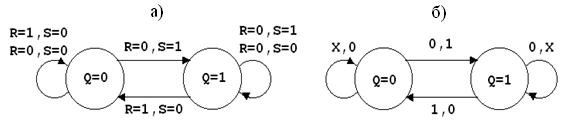
Рис. 4.7. Граф RS–триггера на элементах ИЛИ–НЕ:

а) полное представление; б) сокращенное представление

На рис. 4.7,б тот же граф триггера нарисован более компактно. Входные сигналы, которые могут принимать любые значения (как 0, так и 1), обозначены как Х, а позиции обозначения соответствует последовательности R, S.

Довольно часто применяются синхронные RS‑триггеры, которые кроме входов R и S, имеют третий вход – синхровход C. Назначение этого входа – обеспечить одновременность срабатывания многих триггерных схем (обеспечить их синхронную работу).

Для построения синхронного RS‑триггера сигналы R и S в уравнениях асинхронных триггеров надо заменить на RC и SC соответственно.

На рис. 4.8 показан синхронный RS‑триггер на элементах И‑НЕ. При C = 1 состояние триггера определяется сигналами на RS–входах. При C = 0 триггер хранит последнее состояние, независимо от сигналов на входах R и S.

На рис. 4.9 показан синхронный RS‑триггер на элементах ИЛИ‑НЕ. При = 0 состояние триггера определяется сигналами на –входах . При = 1 триггер хранит прежнее состояние, независимо от сигналов на входах и .

Р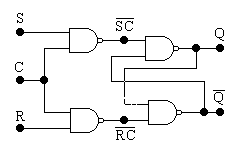 ис. 4.8. Синхронный RS‑триггер на элементах И‑НЕ

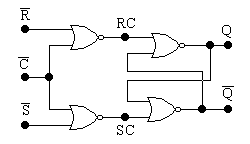
Рис. 4.9. Синхронный ‑триггер на элементах ИЛИ‑НЕ

1.3. JK–триггер

JK–триггер имеет более сложную, по сравнению с RS–триггером, структуру и более широкие функциональные возможности. Помимо информационных входов J и К и прямого и инверсного выходов Q и , JK–триггер имеет вход управления С (этот вход также называют счетным или синхровходом), а также асинхронные установочные R и S входы, как у RS‑триггера. Обычно активными уровнями установочных сигналов являются нули, как в схеме на рис. 4.2, тогда на схемах они обозначаются с инверсиями и . Асинхронные входы имеют приоритет над остальными. Активный уровень сигнала на входе S устанавливает триггер в состояние Q = 1, а активный уровень сигнала на входе R – в состояние Q = 0, независимо от сигналов на остальных входах.

Если на входы установки одновременно подать пассивный уровень сигнала, то состояние триггера будет изменяться по синхросигналу на счетном входе в зависимости от состояния входов J и К, как показано в таблице переходов (табл. 4.7).

Таблица 4.7

Таблица переходов JK–триггера

J	K	Qt+1
0	0	Qt
0	1	0
1	0	1
1	1

При неактивном уровне сигнала С триггер находится в режиме хранения и не реагирует ни на какие другие входы, кроме и .

Работа JK–триггера аналитически описывается следующим уравнением:

.

(Заметим, это уравнение соответствует четвертой минимальной форме RS–триггера, если заменить S на J, а R на K.)

Один из вариантов схемы двухступенчатого JK–триггера с запрещающими связями и входами установки , а также его условное графическое обозначение приведены на рис. 4.10,а,б.

Другой вариант схемы двухступенчатого JK–триггера с инвертором показан на рис. 4.10,в. Его условное графическое обозначение совпадает с обозначением предыдущего триггера (см. рис. 4.10,б).

Если во второй ступени использовать синхронный ‑триггер на элементах ИЛИ‑НЕ, то инвертор на синхровходе второй ступени можно исключить, правда, придется поставить два инвертора на входы R, S второй ступени(см. рис. 4.10,г).

Поскольку в рассматриваемых триггерных структурах имеется две ступени, два варианта структурной схемы триггеров (с запрещающими связями и с инвертором) и два типа RS–триггеров, то возможно построение восьми вариантов таких структур (см. рис. 4.11,а…4.11,з). (Правда, если учесть, что комбинационные части на входах RS–триггеров можно реализовать в любом базисе, то число триггерных структур оказывается много больше.)

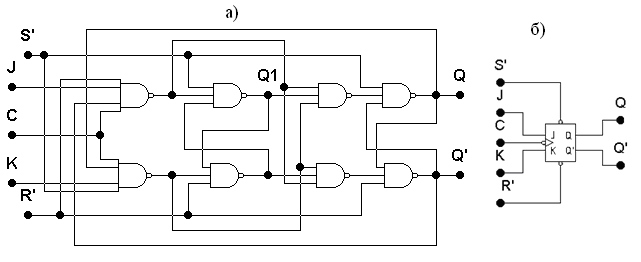
Рис. 4.10. Двухступенчатый JK–триггер с запрещающими связями:

а) функциональная схема; б) обозначение

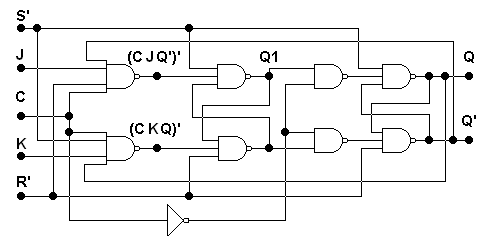
Рис. 4.10,в. Двухступенчатый JK–триггер с инвертором

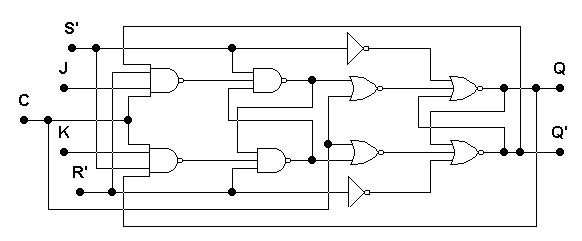
Рис. 4.10,г. Двухступенчатый JK–триггер на элементах двух типов

На рис. 4.11.а…4.11,з обозначено: ЗЯ1, ЗЯ2 – RS–триггеры первой и второй ступени (могут быть разных типов), КС1 и КС2 – комбинационные логические схемы на входах RS–триггеров первой и второй ступени.

Временные диаграммы работы JK–триггера при R = S = 1 приведены на рис. 4.12. Обратите внимание на то, что все изменения выхода происходят только в момент отрицательного перепада (среза) синхросигнала С. Если J = K = 1, тo с каждым новым тактовым импульсом выход будет изменять свое значение на противоположное, а триггер будет выполнять функцию делителя частоты на 2.

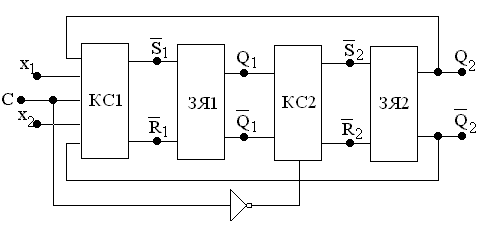
Рис. 4.11,а

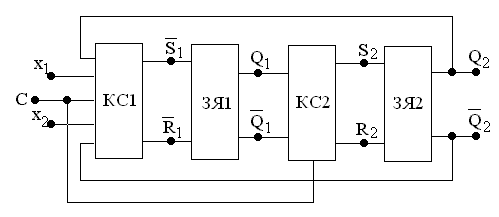
Рис. 4.11,б

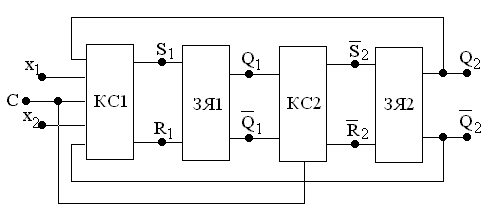
Рис. 4.11,в

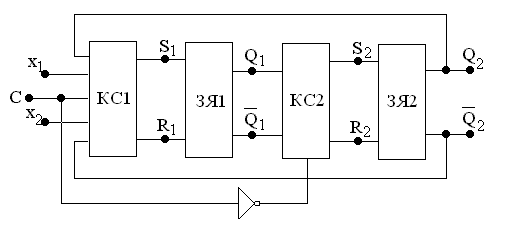
Рис. 4.11,г

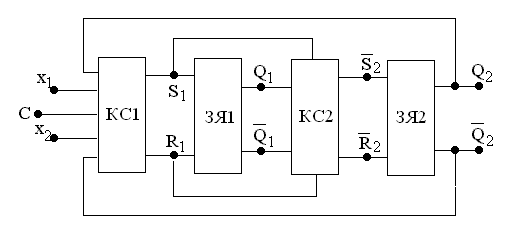
Рис. 4.11,д

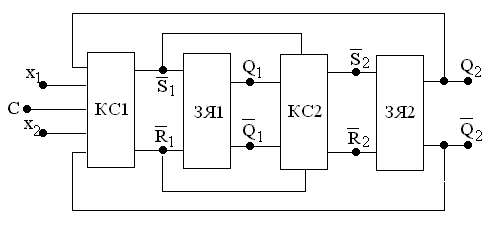
Рис. 4.11,е

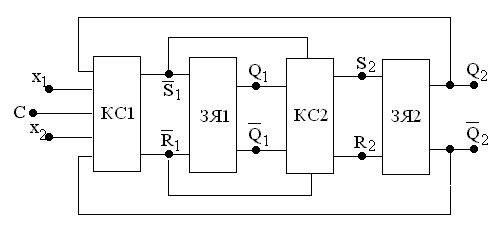
Рис. 4.11,ж

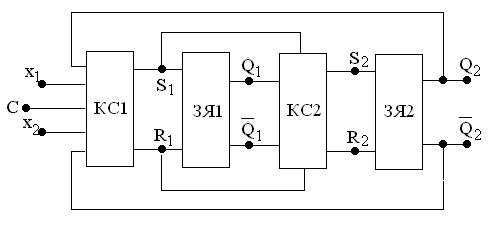
Рис. 4.11,з

Р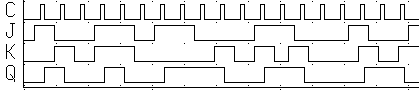 ис. 4.12. Временная диаграмма переключений

двухступенчатого JK–триггера

Подобно RS–триггеру, изменения состояний JK–триггера можно изобразить графом переходов (рис. 4.13). Входные сигналы, которые могут принимать любые значения (как 0, так и 1), на рисунке обозначены как Х, а позиции обозначения соответствует последовательности J, К.

Р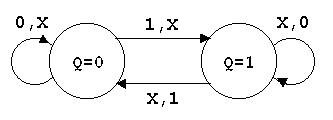 ис. 4.13. Граф переходов JK–триггера

1.4. D–триггер

Следует различать простой D–триггер «защелку» и сложный – универсальный D–триггер, срабатывающий по перепаду 0-1 на синхровходе С. Оба эти триггера синхронные, но D–триггер «защелка» построен на одном RS–триггере и управляется уровнем сигнала С (рис. 4.14). Он имеет два входа D и C. При С = 1 любое изменение D–входа вызывает изменение выхода Q (это недостаток данного триггера).

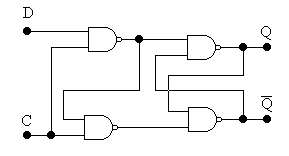
Рис. 4.14. Простой D–триггер

Универсальный D–триггер (рис. 4.15) состоит из трех RS–триггеров (из шести элементов), имеет информационный вход D, вход синхронизации С и, возможно, установочные входы R и C (рис. 4.16).

Информация со входа D заносится в триггер по положительному перепаду 0-1 (по фронту) импульса С и сохраняется на выходе Q до следующего положительного перепада на входе С, поэтому любые изменения на входе D, возникающие между этими событиями, не проходят на выход.

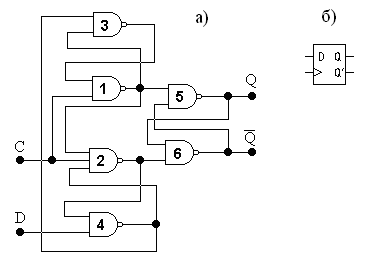
Рис. 4.15. D–триггер, работающий по фронту синхросигнала (а),

и его обозначение (б)

Асинхронные входы имеют приоритет, поскольку устанавливают триггер в требуемое состояние независимо от сигналов на входах С и D.

Функционирование обоих типов D–триггера описывается таблицей переходов (табл. 4.8) и похожими временными диаграммами сигналов (рис. 4.17). Отличие диаграмм заключается в том, что у простого триггера изменения сигнала D при С = 1, проходят на выход, а у универсального триггера нет.

Р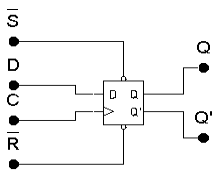 ис. 4.16. Универсальный D–триггер с установочными входами

Таблица 4.8

Таблица переходов

D–триггера

D	Qt+1
0	0
1	1

Аналитически работа D–триггера может быть описана следующим простым уравнением:

Q_{t + 1} = D.

Уравнение показывает, что состояние триггера на t+1–ом такте равно значению входного сигнала в момент, предшествующий фронту сигнала С.

Р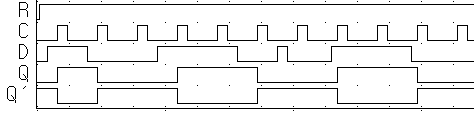 ис. 4.17. Временная диаграмма D–триггера

Другой вариант функциональной схемы D–триггера может быть получен из схемы JK–триггера (рис. 4.10,а) путем подключения сигнала D к входу J непосредственно, а к входу К – через инвертор.

1.5. Т–триггер (счетный триггер)

На основе JK–триггеров и универсальных D–триггеров можно построить схемы, осуществляющие так называемый счетный режим. Такие схемы называют Т–триггерами или счетными триггерами, связывая с этим способ их функционирования. На рис. 4.18 представлены схемы построения Т–триггера на основе JK– и D–триггеров.

Счетный режим работы двухступенчатого Т–триггера, переключаемого срезом сигнала С (рис. 4.18,а), иллюстрируется временными диаграммами рис. 4.19.

В двухступенчатом JK–триггере, имеющем асинхронные R– и S– входы с активным низким уровнем, счетный режим реализуется путем подачи констант J = K = 1 и R = S = 1 и входного сигнала Т на вход С. Тогда в соответствии с таблицей переходов JK–триггера (табл. 4.7) по каждому срезу входного сигнала Т состояние триггера будет изменяться на противоположное.

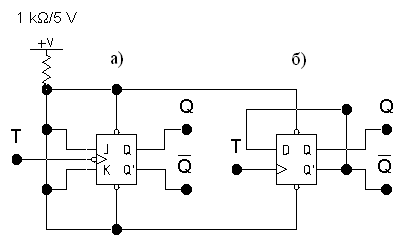
Рис. 4.18. Т–триггер: а) на базе двухступенчатого JK–триггера;

б) на базе D–триггера, переключаемого фронтом сигнала С

Р ис. 4.19. Временная диаграмма работы двухступенчатого Т–триггера

В D–триггере, переключаемом фронтом сигнала С, счетный режим реализуется при помощи обратной связи (на вход D подается сигнал с инверсного выхода). Следовательно, при каждом положительном перепаде сигнала на счетном входе Т состояние выхода будет изменяться на противоположное. В результате на каждые два входных тактовых импульса Т–триггер формирует один импульс выходного сигнала Q, то есть осуществляет деление частоты f_t на его входе Т на 2

f_Q = f_t/2 ,

где f_Q — частота следования импульсов на выходе триггера.