4. Реализация логических функций на мультиплексорах

Полностью определенная логическая функция n переменных определена для 2ⁿ комбинаций значений переменных. Ее можно реализовать на мультиплексоре, имеющем n управляющих и 2ⁿ информационных входов. В этом случае каждой комбинации значений аргументов соответствует единственный информационный вход мультиплексора, на который подается соответствующее значение функции.

Пусть требуется реализовать функцию

F₁ = ,

таблица истинности которой показана в табл. 3.2.

Таблица 3.2

№	С	B	А	F1
0	0	0	0	1
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	0
6	1	1	0	1
7	1	1	1	1

Эта функция зависит от трех переменных, поэтому она определена для 8 комбинаций значений переменных и ее можно записать так

Уравнение мультиплексора с тремя управляющими входами MS 8–1 имеет вид

Как видим, структура уравнений полностью совпадает, поэтому данную функцию можно реализовать на мультиплексоре MS 8-1 с тремя управляющими входами A, B, C, подав на информационные входы D₀, …, D₇ соответствующие значения функции.

В данном случае на входы с номерами 1, 2, 4, 5 следует подать уровень логического нуля, а на остальные – уровень логической единицы, т.е.

D₀ = 1, D₁ = 0, D₂ = 0, D₃ = 1, D₄ = 0, D₅ = 0, D₆ = 1, D₇ = 1.

Таким образом, при изменении комбинаций логических уровней на управляющих входах мультиплексора к его выходу будут подключаться входы, значения сигналов на которых равны соответствующим значениям функции. Схемная реализация приведена на рис. 3.8.

В общем случае можно сформулировать следующее правило:

если количество логических переменных n, от которых зависит реализуемая логическая функция, совпадает с разрядностью адресной части мультиплексора, то эти переменные подаются на адресные входы мультиплексора (старшая переменная - на старший адресный вход), а на информационные входы мультиплексора MS 2ⁿ–1 – константы 0 и 1 в соответствии с таблицей истинности реализуемой функции.

Р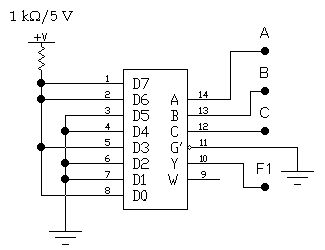 ис. 3.8. Реализация функции F₁ на мультиплексоре 8-1

При реализации логических функций на информационные входы можно подавать не только константы, но и изменяющиеся входные сигналы. Например, функцию F₁, рассмотренную выше, можно реализовать по-другому следующим образом.

Минимизируем выражение функции. В результате получим

F₁= .

Составим таблицу истинности функции в зависимости от значений переменных а и b (см. табл.3.3).

Таблица 3.3

N	B	A	F1
0	0	0
1	0	1	0
2	1	0	С
3	1	1	1

Заданную такой таблицей функцию реализуют на мультиплексоре, как и в предыдущем случае, подав на вход с номером N сигнал, уровень которого соответствует значению функции F₁. В данном случае сигналы С и , соответствующие переменной С, подаются на информационные входы так, как указано в таблице истинности. При этом сокращается число управляющих входов.

Схемная реализация такого способа задания функции представлена на рис. 3.9.

Так как используются только два адресных входа, то управляющий вход С можно заземлить. При этом состояние информационных входов D4,…,D7 безразлично.

Схема рис. 3.9 по существу представляет собой мультиплексор 4-1 с двумя управляющими и четырьмя информационными входами.

Если функцию можно представить в виде произведения одночлена на многочлен, то ее также можно реализовать при помощи мультиплексора с уменьшенным числом управляющих входов. Как следует из уравнения мультиплексора, сигнал, соответствующий одночлену, нужно подать на вход разрешения. Например, требуется реализовать на мультиплексоре 8-1 функцию F₂ шести переменных, описываемую следующим выражением

F₂=

При реализации данной функции на мультиплексоре сигнал, соответствующий переменной Х, следует подать на его разрешающий вход.

Рассмотрим, какие сигналы необходимо подать на управляющие входы мультиплексора. Выражение в скобках можно рассматривать как некоторую функцию F пяти переменных А, B, С, D, E, из которых наиболее часто используются переменные А, B и С. Поэтому сигналы, соответствующие этим переменным, целесообразно подать на три управляющих входа мультиплексора MS 8-1.

Р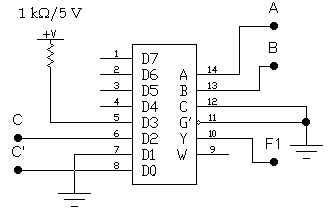 ис. 3.9. Второй вариант реализации функции F1

Определим, какие сигналы следует подать на информационные входы, чтобы реализовать функцию F₂. Для этого составим таблицу истинности функции в зависимости от значений переменных А, B и С (табл. 3.4).

Таблица 3.4

N	С	B	А	F
0	0	0	0	0
1	0	0	1	D
2	0	1	0	0
3	0	1	1	E
4	1	0	0	D
5	1	0	1	D
6	1	1	0	0
7	1	1	1	1

Из таблицы видно, что на информационные входы с номерами N = 0, 2, 6 нужно подать уровень логического нуля. Сигнал, соответствующий переменной D, нужно подать на входы с номерами N = 1, 4, 5, а сигнал, соответствующий переменной Е, – на вход с номером 3. Схемная реализация функции шести переменных F2 представлена на рис. 3.10.