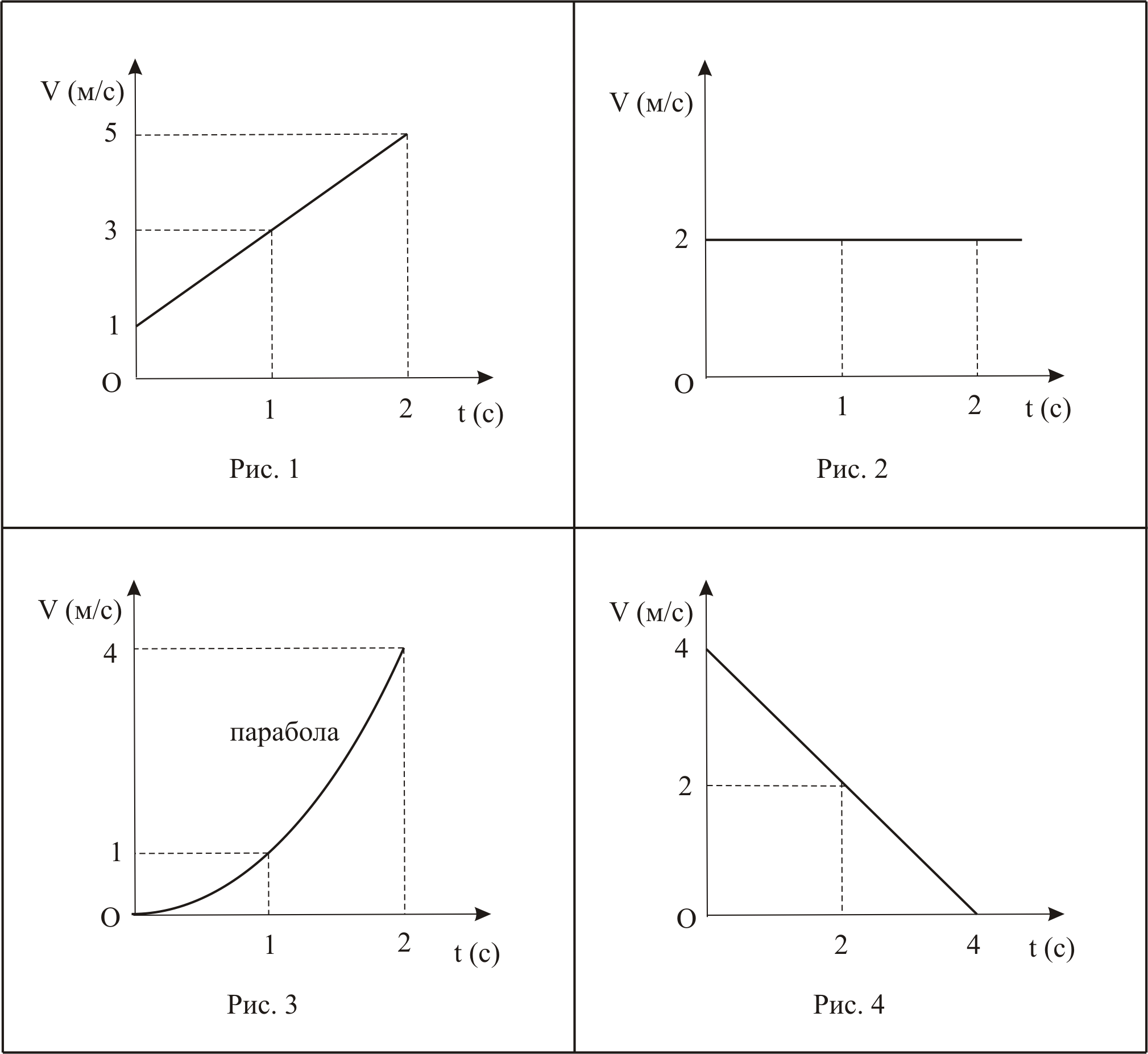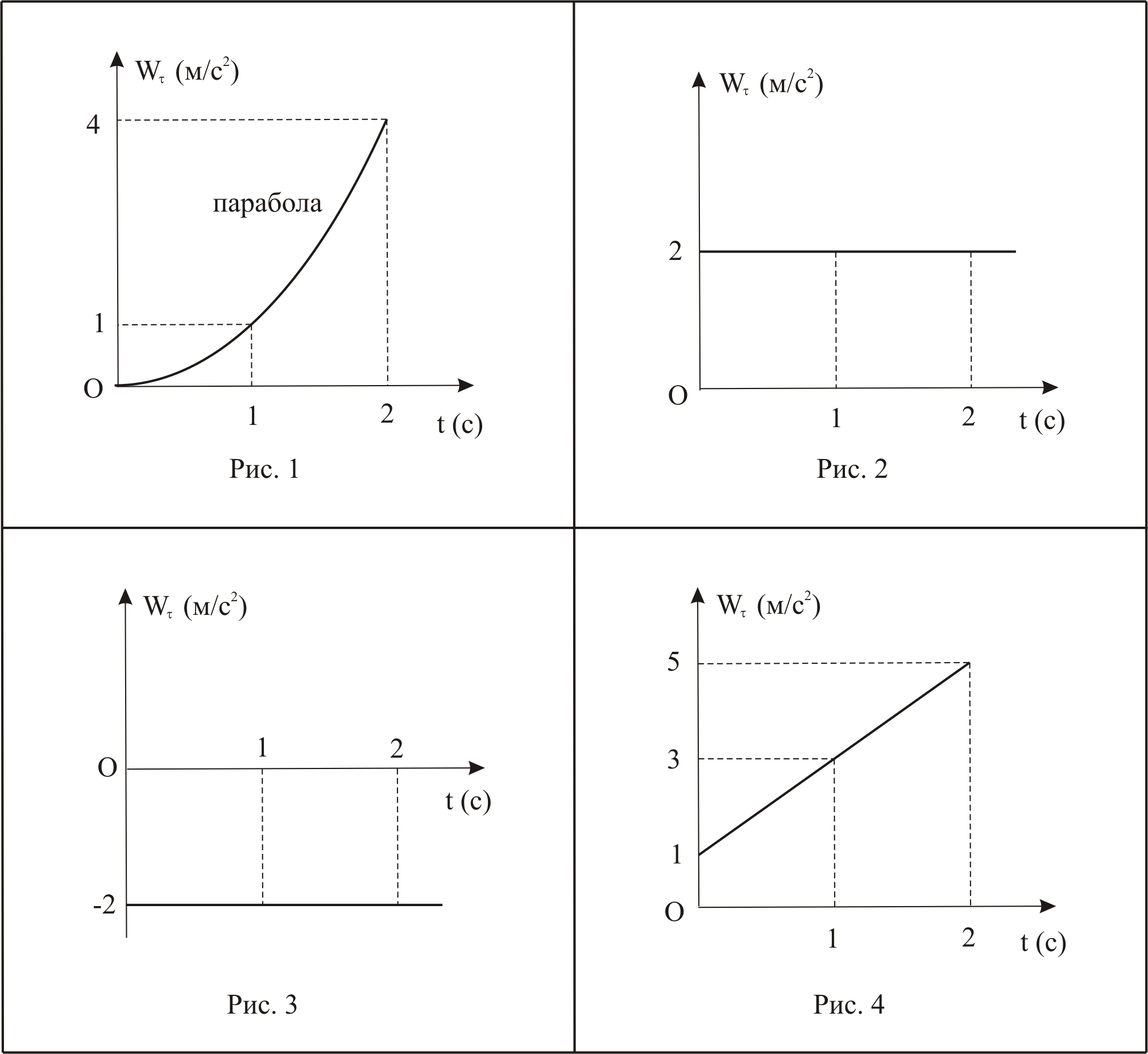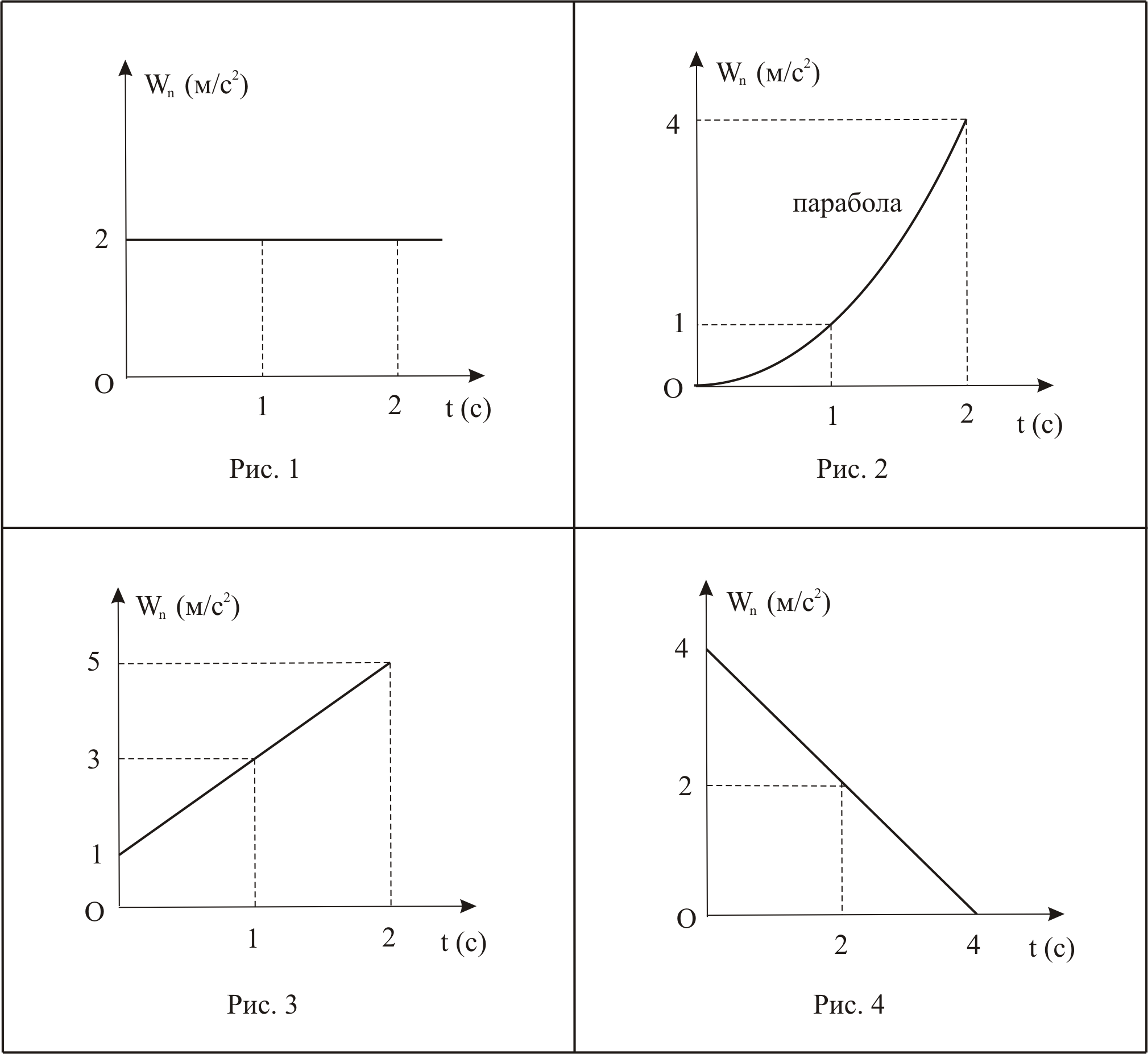Кинематика. Задание № 16 – Частные случаи движения точки

	16.1 На рисунках представлены графики зависимости модуля скорости движущейся точки от времени. Равноускоренному движению точки соответствует график на … (Рис. 1) Решение При равноускоренном движении касательное ускорение точки постоянно и отлично от нуля. Зависимость модуля скорости от времени для равноускоренного движения имеет вид . Данной зависимости соответствует график на Рис.1.
	16.2 На рисунках представлены графики зависимости модуля скорости движущейся точки от времени. Равномерному движению точки соответствует график на … (Рис. 2) Решение При равномерном движении касательное ускорение точки равно нулю, а модуль скорости постоянен. Равномерному движению точки соответствует график на Рис. 2.
	16.3 Точка движется в сторону возрастания дуговой координаты . На рисунках представлены графики зависимости дуговой координаты точки от времени. Равноускоренному движению точки соответствует график на … (Рис. 1) Решение При равноускоренном движении касательное ускорение точки постоянно и отлично от нуля. Зависимость дуговой координаты от времени для равноускоренного движения имеет вид . Данной зависимости соответствует график на Рис.1.
	16.4 Точка движется в сторону возрастания дуговой координаты . На рисунках представлены графики зависимости дуговой координаты точки от времени. Равнозамедленному движению точки соответствует график на … (Рис. 2) Решение При равнозамедленном движении касательное ускорение точки постоянно и отлично от нуля. Зависимость дуговой координаты от времени для равнозамедленного движения имеет вид . Данной зависимости соответствует график на Рис.2.
	16.5 Точка движется в сторону возрастания дуговой координаты . На рисунках представлены графики зависимости касательного ускорения точки от времени. Равноускоренному движению точки соответствует график на … (Рис. 2) Решение При равноускоренном движении касательное ускорение точки постоянно и отлично от нуля. В случае, когда точка движется в сторону возрастания дуговой координаты , касательное ускорение должно быть больше нуля. Отсюда следует, что правильный ответ представлен на Рис.2.
	16.6 Точка движется в сторону возрастания дуговой координаты . На рисунках представлены графики зависимости касательного ускорения точки от времени. Равнозамедленному движению точки соответствует график на … (Рис. 3) Решение При равнозамедленном движении касательное ускорение точки постоянно и отлично от нуля. В случае, когда точка движется в сторону возрастания дуговой координаты , касательное ускорение должно быть меньше нуля. Отсюда следует, что правильный ответ представлен на Рис.3.
	16.7 Точка движется по окружности. На рисунках представлены графики зависимости нормального ускорения точки от времени. Равномерному движению точки соответствует график на … (Рис. 1) Решение Нормальное ускорение при движении точки по окружности радиуса равно . Отсюда следует, что при равномерном движении точки по окружности, нормальное ускорение должно быть постоянно, т.к. модуль скорости не меняется. Правильный ответ представлен на Рис.1.
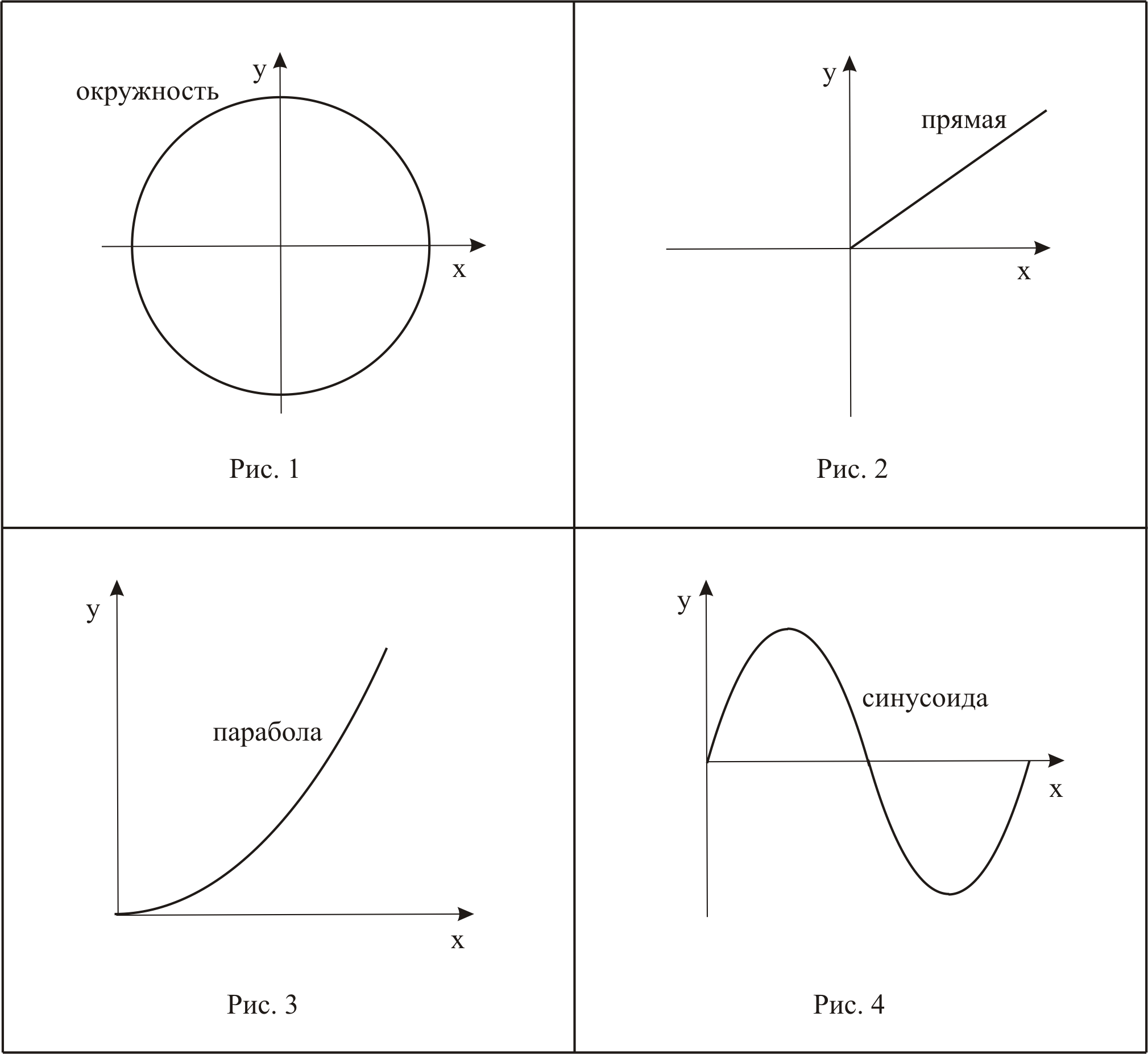
	16.8 На рисунках представлены графики зависимости модуля скорости движущейся точки от времени. Равнопеременному движению точки соответствует график на … (Рис. 1) Решение При равнопеременном движении точки скорость за равные промежутки времени меняется одинаково. Это соответствует зависимости модуля скорости от времени, показанной на Рис.1.
	16.9 Скорость точки и её нормальное ускорение постоянны по модулю и отличны от нуля. Точка движется по траектории, показанной на … (Рис. 1) Решение При движении точки по криволинейной траектории . Так как нормальное ускорение и модуль скорости точки постоянны, то радиус кривизны траектории в любой её точке также постоянен. Следовательно, правильный ответ показан на Рис.1.
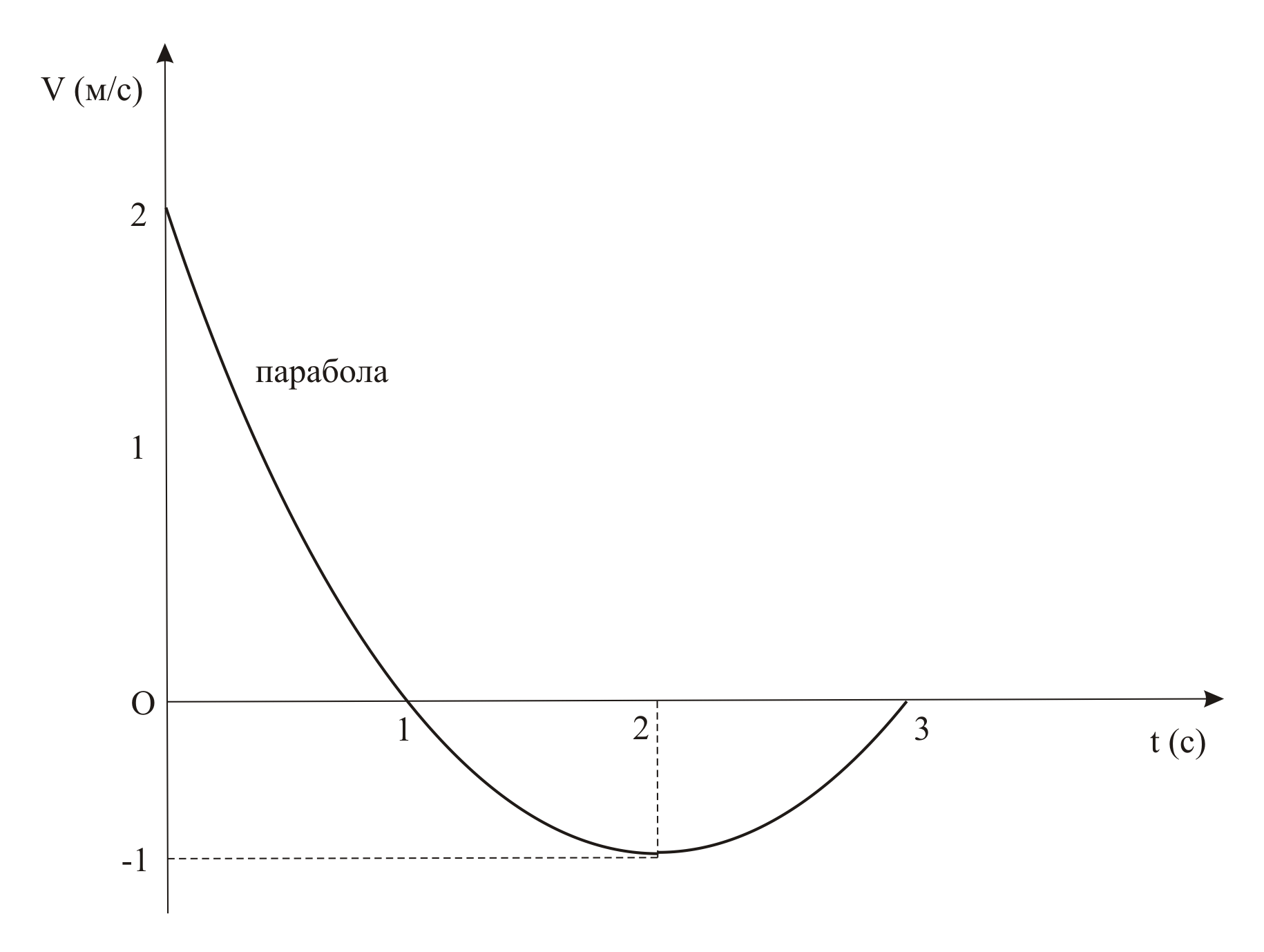
	16.10 На рисунке дан график зависимости от времени проекции скорости точки на касательную к траектории. Касательное ускорение точки равно нулю в момент времени … (2 с) Решение Касательное ускорение точки равно . Так как является производной по времени от , то равно нулю в точках минимума или максимума функции . Правильный ответ .
	16.11 На рисунке дан график зависимости дуговой координаты точки от времени. Нормальное ускорение точки равно нулю в момент времени … (2 с) Решение Дуговая координата точки и скорость связаны зависимостью . Отсюда видно, что скорость обращается в нуль в моменты времени, когда дуговая координата достигает минимума или максимума ( является производной дуговой координаты s). Следовательно, в момент времени с скорость равна нулю. Нормальное ускорение точки равно . Отсюда видно, что равно нулю в момент времени 2 с. Правильный ответ .