Динамика. Задание № 31 – Теорема об изменении кинетической энергии

31.1

Тело брошено с поверхности Земли вертикально вверх с начальной скоростью

. Сопротивление воздуха не учитывается. Максимальная высота, на которую поднимется тело, равна… (8 м)

2 м, 4 м, 6 м, 8 м

Решение

mv²/2 - mv₀²/2 = -mgh,

v = 0,

h = v₀²/2g = 16g/2g = 8 (м).

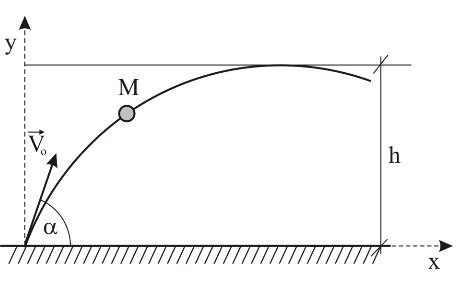
31.2

Тело брошено с поверхности Земли под углом к горизонту с начальной скоростью . Сопротивление воздуха не учитывается. Максимальная высота, на которую поднимется тело, равна…(4 м)

2 м, 3 м, 4 м, 5 м

Решение

mv²/2 - mv₀²/2 = -mgh,

v = v₀ ·cos α (так как в верхней точке имеем лишь горизонтальную составляющую скорости), подставляя, получим v₀²(cos²α - 1) = -2gh,

h = v₀² ·sin²α/2g = 16g/4g = 4 (м).

31.3

Тело брошено с поверхности Земли под углом к горизонту с начальной скоростью . Сопротивление воздуха не учитывается. Максимальная высота, на которую поднимется тело, равна… (2 м)

31.4

В начальный момент времени математический маятник отклонён от вертикали на угол

и отпущен без начальной скорости. Длина нити . Скорость точки в момент прохождения положения равновесия равна...

( )

, ,

,

Решение

mv²/2 - mv₀²/2 = mgh,

h = OM - OM·cos 60⁰ = OM/2,

v₀=0,

м/с.

31.5

В начальный момент времени математический маятник отклонён от вертикали на угол

и отпущен без начальной скорости. Длина нити . Скорость точки в момент прохождения положения равновесия равна...

( )

31.6

В начальный момент времени математический маятник отклонён от вертикали на угол

и отпущен без начальной скорости. Длина нити . Скорость точки в момент прохождения положения равновесия равна...

( )

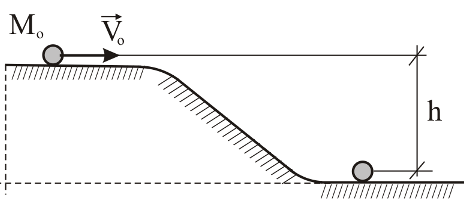
31.7

Тело движется по горизонтальной плоскости со скоростью . Трением пренебрегаем. При движении по горизонтальной плоскости, расположенной ниже на , скорость тела будет равна…

( )

, , ,

Решение

mv²/2 - mv₀²/2 = mgh, v² = v₀² + 2gh = 9g, v = 3 м/с.

31.8

Минимальная скорость , которую должно иметь тело, чтобы подняться без сопротивления на высоту , равна… ( м/с)

, , ,

Решение

mv²/2 - mv₀²/2 = -mgh, v = 0, v ₀= м/с.

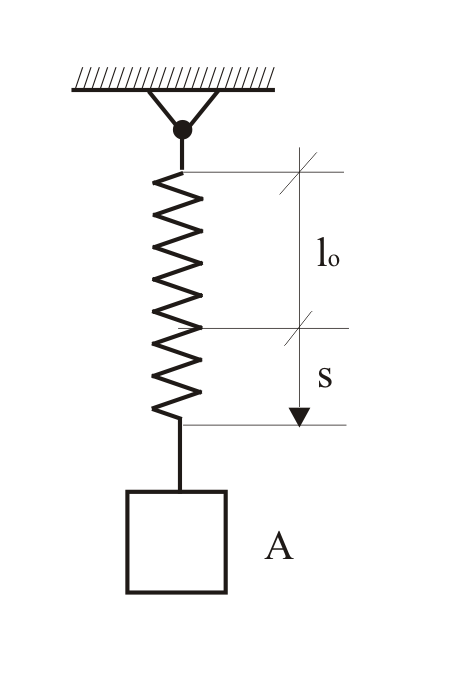
31.9

Груз массы подвешен к концу пружины, жёсткость которой . В начальный момент пружина растянута на и груз отпущен без начальной скорости. Скорость груза в тот момент времени, когда пружина не растянута, равна…

(0)

0, 1 м/с, 2 м/с, 3 м/с

Решение

mv²/2 - mv₀²/2 =

= (c/2)·(λ₀² - λ₁²) - mgh,

λ ₀= s, λ₁ = 0, h = s

,

v²=(c/m)·s² - 2gs=0,

v=0.

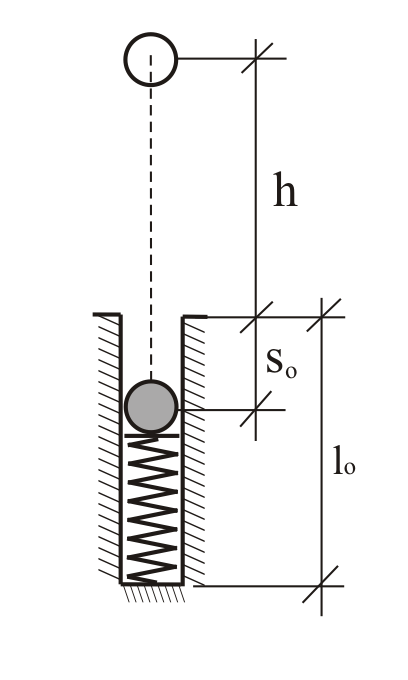
31.10

Пружина жёсткости сжата на величину . Высота , на которую поднимется шарик массой , выброшенный пружиной, равна…

(2 м)

1 м, 2 м, 3 м, 4 м

Решение

mv²/2 – mv₀²/2 =

= (c/2)·(λ₀² – λ₁²) –

– mg(h+s₀),

v = 0, v₀ = 0,

λ₀ = s₀, λ₁ = 0,

h=cs₀²/2gm – s₀ =

= 8g/2g – 2 = 2 м.

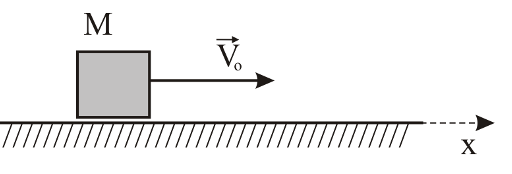
31.11

Тело скользит по горизонтальной плоскости. В данный момент времени скорость тела равна . Тело тормозится силой трения; коэффициент трения равен . Расстояние, которое пройдёт тело до остановки, равно…

(80 м)

65 м, 70 м, 75 м, 80 м

Решение

.

Учитывая, что конечная скорость тела равна 0, получаем

. Отсюда .

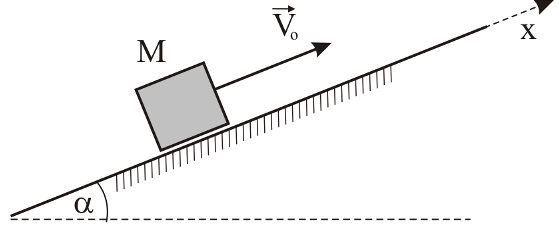
31.12

Тело скользит вверх по наклонной плоскости, наклонённой под углом к горизонту. В начальный момент времени скорость тела равна . Трением пренебречь. Расстояние, которое пройдёт тело до остановки, равно…

( )

, , , ,

Решение

.

Учитывая, что конечная скорость тела равна 0, получаем

. Отсюда .

31.13

Тело скользит вверх по наклонной плоскости, наклонённой под углом к горизонту. В начальный момент времени скорость тела равна .Трением пренебречь. Расстояние, которое пройдёт тело до остановки, равно… ( )

31.14

Тело скользит вверх по наклонной плоскости, наклонённой под углом к горизонту. В начальный момент времени скорость тела равна . Трением пренебречь. Расстояние, которое пройдёт тело до остановки, равно… (16 м)