Государственное образовательное учреждение высшего профессионального образования

Санкт-Петербургский государственный морской технический университет

«СЕВМАШВТУЗ»

Кафедра № 15

«Промышленное и гражданское строительство верфи»

Дисциплина: "Строительная механика и прочность корабля"

Расчётно-графическая работа № 2

«Расчёт параметров изгиба однопролётной балки со свободно опёртым и упруго защемленным концами»

Учебная группа № 1301

Вариант задания № 11

Работу выполнил:

Студент: Махрова О.А.

Фамилия И.О.

_____________ “___”______2011 г.

подпись

Работу принял:

Преподаватель: Рижинашвили Г.М.

Фамилия И.О.

_____________ “___”______2011 г.

подпись

Северодвинск

2011 г.

Содержание пояснительной записки РГР №2

1. Расчётная схема конструкции однопролётной балки с призматическим и непризматическим участками.

2. Исходные данные.

3. Исходное выражение для определения значений изгибающих моментов в сечениях балки через значения коэффициента опорной пары (берётся из РГР №1).

4. Аналитическое определение значения изгибающего момента в опорном упруго защемлённом сечении балки.

5. Построение эпюры изгибающих моментов по длине балки с изображением условия определения длины призматического участка (рис. 2).

6. Аналитическое определение экстремального значения изгибающего момента в пролёте балки.

7. Получение уравнения для определения длины призматического участка.

8. Аналитическое решение уравнения для определения длины призматического участка.

9. Исходное выражение для определения значений перерезывающих сил в сечениях балки через значения коэффициента опорной пары (берётся из РГР №1).

10. Построение эпюры перерезывающих сил по длине балки с изображением длины призматического участка (рис. 3).

11. Расчёт величины экстремального значения изгибающего момента в пролёте балки.

12. Расчёт величины наибольшего значения перерезывающей силы в районе призматического участка балки.

13. Подбор прокатного профиля по заданному значению момента инерции проектируемой балки.

14. Расчёт величины наибольших значений нормальных напряжений, возникающих от изгиба балки в районе призматического участка балки.

15. Расчёт величины наибольших значений касательных напряжений, возникающих от изгиба балки в районе призматического участка балки.

16. Условия прочности проектируемой балки по нормальным и касательным напряжениям.

17. Выбор марки материала балки из сплавов, применяемых для изготовления корпусов судов.

18. Чертёж конструкции спроектированной однопролётной балки (рис. 4).

Примечания:

1. Пояснительная записка оформляется на листах формата А-4 (с одной стороны).

2. Графики (рис.2 и рис. 3), а также чертёж конструкции спроектированной однопролётной балки (рис. 4) строятся на отдельном листе.

3. Для всех размерных величин в тексте пояснительной записки, в таблицах и на графиках должны указываться размерности.

4. Рисунки должны иметь названия, а также должны иметь номера, на которые в тексте пояснительной записки должны быть ссылки.

5. Построение эпюры значений изгибающих моментов должно быть произведено для 21-го сечения с шагом δX=0.05 L.

6. Построение эпюры перерезывающих сил должно быть произведено на основании значений, рассчитанных в двух сечениях (при X=0 и X=L).

7. На чертёже конструкции спроектированной балки (рис. 4) должны быть указаны геометрические параметры подобранного прокатного профиля, размеры длины балки и призматического участка, размеры бракеты (кницы) в районе упруго защемлённого сечения балки.

1 . Расчётная схема однопролётной балки.

or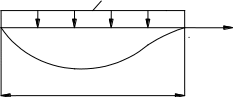

0

x

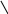
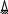
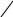ЕI

L

W(x)

y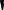

Рис. 1 Расчётная схема однопролётной балки

2. Исходные данные.

В качестве исходных данных задаются значения следующих величин:

L = 8 м - длина балки;

q = 30 кгс/см - интенсивность равномерно распределённой нагрузки;

Е = 210000 МПа - модуль нормальной упругости материала балки;

J = 8000 см⁴ - момент инерции поперечного сечения балки;

= 0,99 - коэффициент опорной пары , характеризующий степень

податливости упругого защемления правого конца балки.

3. Выражение для определения значений изгибающих моментов в сечениях балки через значения коэффициента опорной пары.

4. Аналитическое определение значения изгибающего момента в опорном упруго защемлённом сечении балки.

Величины и , полученные в РГР №1, пункт 21, имеют значение:

;

.

Значение опорного изгибающего момента в районе упругого защемления будет равно:

5. Построение эпюры изгибающих моментов по длине балки с изображением условия определения длины призматического участка.

Для построения эпюры значений изгибающих моментов М(х) воспользуемся данными, полученными в РГР №1, пункт 21.

М

L_пр.= 7264

L_пр.= 8000

Рис. 2 Эпюра изгибающих моментов М(х) с изображением призматического участка.

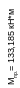
6. Аналитическое определение экстремального значения изгибающего момента в пролете балки.

7. Получение уравнения для определения длины призматического участка.

Учитывая характер распределения значений изгибающих моментов по длине балки, приведенный на (рис. 2). Можно определить протяженность такого призматического участка , отсчитываемого от левой абсолютно жёсткой свободной опоры при х = 0, в пролёте которого действует изгибающий момент ,а на его правом конце (при х = ) действует изгибающий момент М( ). Численное значение которого по своей абсолютной величине равно значению изгибающего момента :

Тогда на протяжении призматического участка Lпр профиль поперечного сечения балки будет определён на основании значений изгибающего момента М( ) и перерезывающей силы N( ), меньших по своим абсолютным значениям, чем соответствующие наибольшие значения изгибающего момента М(L) и перерезывающей силы N(L).

Учитывая формулы

и

уравнения запишется в виде:

,

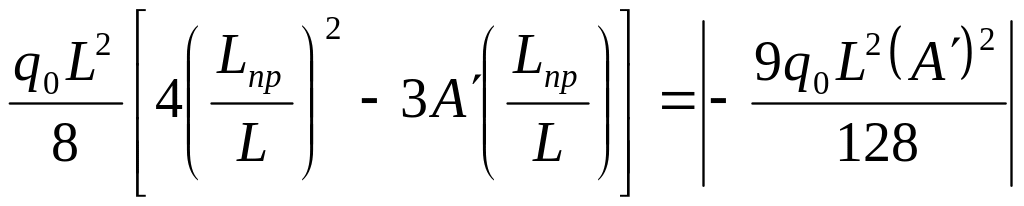которое после преобразований приводит к следующему алгебраическому уравнению второго порядка относительно искомой величины протяженности призматического участка :

.

Решение уравнения приводит к следующему выражению, определяющему значение величины :

8. Аналитическое решение уравнения для определения длины призматического участка.

Решение уравнения из п.7 приводит к следующему выражению, определяющему значение величины :

,

или по отношению к общей длине балки:

9. Исходное выражение для определения значений перерезывающих сил в сечениях балки через значения коэффициента опорной пары.

10. Построение эпюры перерезывающих сил по длине балки с изображением длины призматического участка

Для построения эпюры перерезывающих сил N(х) воспользуемся данными, полученными в РГР №1, пункт 21.

N

L_пр.= 7264

L_пр.= 8000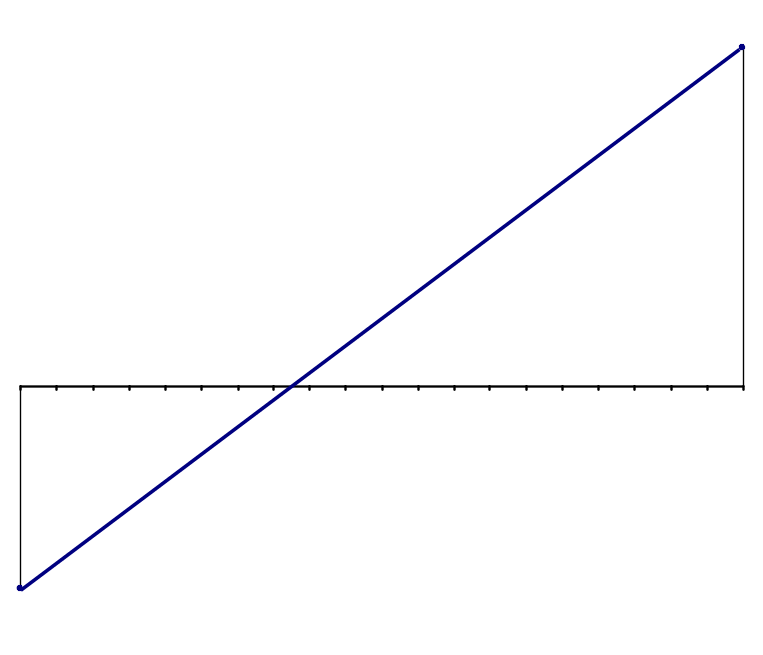

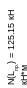
Рис. 3 Эпюра перерезывающих сил N(х) с изображением призматического участка.

11. Расчет величины экстремального значения изгибающего момента в

пролете балки

В качестве расчетной величины для изгибающего момента принимаем значение изгибающего момента равного М( ):

12. Расчет величины наибольшего значения перерезывающей силы в районе призматического участка балки.

В качестве расчетной величины для перерезывающей силы принимаем значение перерезывающей силы, равной N( ), действующей на конце призматического участка при х = :

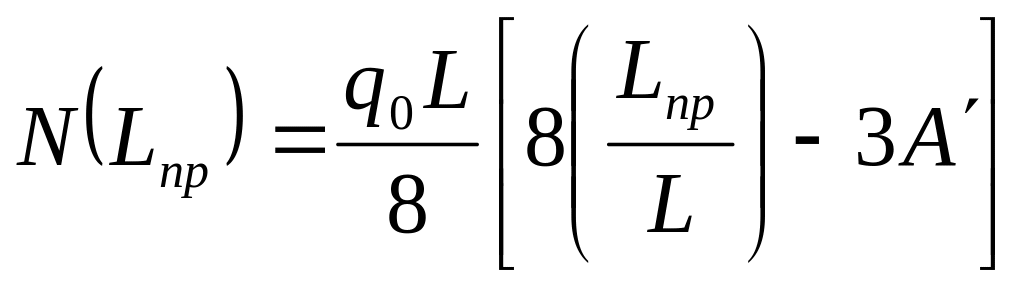
13. Подбор прокатного профиля по сортаменту.

Подбор профиля поперечного сечения балки осуществляем по заданному значению момента инерции поперечного сечения рассматриваемой однопролетной статически неопределимой балки. Исходя из заданного значения момента инерции поперечного сечения балки J=8000(см⁴) подбираем профиль поперечного сечения по действующему сортаменту по ГОСТ 8239-89 (балки двутавровые) профиль № 33, имеющий следующие параметры:

-момент инерции поперечного сечения балки J = 9840 (см⁴);

-высота профиля h = 33(см);

-толщина полки t = 1,12(см);

- толщина стенки S = 0,7(см)

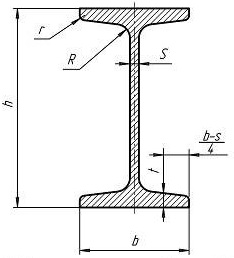
Рис. 4 Поперечное сечение профиля.

- минимальный момент сопротивления поперечного сечения,

- площадь вертикальной стенки воспринимающая перерезывающие силы.