22. Определение максимального значения прогиба балки.

Чтобы найти координату х_пр, где прогиб балки W будет иметь максимальное значение, продифференцируем выражение (22) и прировняем его к нулю:

Решая данное уравнение методом Кардана:

Приведем уравнение к виду ,разделив исходное на 1:

<

получаем x_пр = 0,431

Подставляя это значение в выражение (22) находим максимальное значение прогиба:

23. Определение экстремального значения изгибающего момента в пролёте балки.

Продифференцируя выражение (23) получим

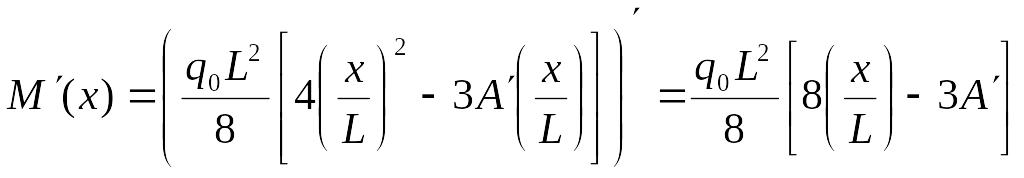. (28)

Тогда значение координаты x_пр, где изгибающий момент будет иметь экстремальное значение M_пр, определится из условия:

или, учитывая выражение (28), из следующего уравнения:

,

откуда

(x_пр) . (29)

Тогда экстремальное значение M_пр будет равно:

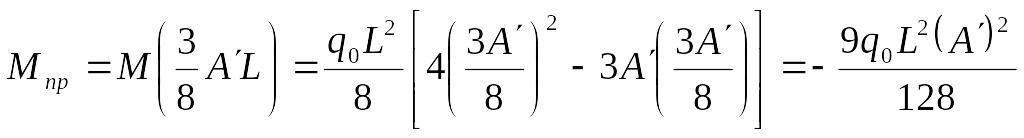; (30)

3