
- •Множества и отображения.
- •Отношения эквивалентности. Факторизация отображений
- •Элементы теории чисел и общей алгебры
- •Введение
- •Элементарная теория чисел
- •II.2. Сравнения в ℤ
- •Функция Эйлера. Теоремы Эйлера, Ферма и др.
- •Функция Мёбиуса. Формула обращения Мёбиуса
- •Сравнения для чисел сочетаний
- •II. Алгебраические структуры
- •II. 1. Множества с бинарными операциями. Группоиды, полугруппы, моноиды
- •Симметрическая и знакопеременная группы
- •Циклические группы
- •Подкольца и идеалы колец.
- •Морфизмы колец.
- •Классы вычетов и факторкольца.
- •Характеристика кольца (поля).
- •Многочлены.
- •Деление многочленов над целостным кольцом.
- •Корни многочленов
- •Производные многочленов. Характеризация корней многочленов
- •Интерполяционная формула Ньютона
- •Интерполяционная формула Лагранжа.
- •Элементы теории полей.
- •Поле разложения.
- •Строение конечных полей.
- •Некоторые результаты о многочленах над конечными полями.
Кугураков В. С.
Теория чисел и общая алгебра
(Материалы к спецкурсу)
Казань- 2009
ВОПРОСЫ К ЗАЧЕТУ
Свойства отображений: инъективность, сюръективность, биективность.
Композиция отображений.
Бинарные отношения. Отношения эквивалентности и порядка.
Основная теорема арифметики кольца ℤ.
Алгоритм деления в ℤ.
Наибольший общий делитель и наименьшее общее кратное.
Свойства сравнений в ℤ.
Полная и приведенная система вычетов по модулю
 .
.Малая теорема Ферма.
Теорема Эйлера.
Китайская теорема об остатках.
Алгебраические структуры: группоиды, полугруппы, моноиды, группы.
Симметрическая и знакопеременная группы.
Теорема Кэли.
Циклические группы. Основные свойства.
Смежные классы по подгруппе.
Теорема Лагранжа.
Подгруппы. Нормальные делители.
Фактор-группа.
Морфизмы групп: изоморфизм и гомоморфизм.
Теорема о гомоморфизмах групп.
Кольца. Определение и общие свойства колец.
Поле. Характеристика поля.
Идеалы колец . Классы вычетов и фактор-кольца.
Кольцо классов вычетов по модулю n.
Теорема о гомоморфизмах колец.
Характеристика кольца и поля.
Простое поле. Два типа простых полей.
Поле отношений.
Интерполяционная формула Лагранжа.
Расширения полей: простое, конечное, алгебраическое, трансцендентное.
Поле разложения многочлена.
Конечное поле. Число элементов. Почему не существует полей порядка 6 и 10, но существуют поля порядков 7 и 9.
Цикличность мультипликативной группы конечного поля.
Неприводимые многочлены над конечными полями. Основная теорема арифметики кольца
 .
.Построение полей малого порядка q (= 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 23,25).
Вычисления в конечных полях.
Содержание
Множества и отображения
Отношения эквивалентности. Факторизация отображений
Упорядоченные множества.пропущено
Элементы комбинаторики. пропущено
Элементы теории чисел и общей алгебры
I. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ЧИСЕЛ
Сравнения в ℤ
Функция Эйлера. Теоремы Эйлера, Ферма и др.
Китайская теорема об остатках
Функция Мёбиуса. Формула обращения Мёбиуса
Сравнения для чисел сочетаний
II. АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ
Множества с бинарными операциями. Группоиды, полугруппы, моноиды
Группы
Симметрическая и знакопеременная группы
Морфизмы групп. Факторгруппы
Циклические группы
Теорема Силова
Кольца
Подкольца и идеалы колец
Морфизмы колец
Характеристика кольца (поля).
Многочлены
Деление многочленов над целостным кольцом
Корни многочленов
Производные многочленов. Характеризация корней многочленов
Элементы теории полей
Поле разложения. Поле отношений
Теорема Кронекера
Строение конечных полей
Некоторые результаты о многочленах над конечными полями
Приложения
Мультипликативная группа целых чисел по модулю n
Литература
Множества и отображения.
Множества. Понятие множества является основным в математике и логике.
Определение. Под множеством понимается любая совокупность объектов, называемых элементами множества, обладающих общим для всех характеристическим свойством.
Замечание.
Георг Кантор ( -
- ),
создатель теории множеств, даёт такое
определение: ″множество
есть многое, мыслимое нами как единое″.
),
создатель теории множеств, даёт такое
определение: ″множество
есть многое, мыслимое нами как единое″.
Эти определения не являются логически строгими, а всего лишь пояснениями, поскольку понятие множества принадлежит к числу первоначальных понятий и не может быть описано с помощью более общего родового понятия, в котором оно выступает в качестве подвида. Множества описываются только при помощи примеров. ∎
Основным
понятием в теории множеств является
понятие принадлежности
элемента множеству. Если объект
 принадлежит множеству
принадлежит множеству
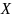 ,
то пишут
,
то пишут
 ,
в противном случае пишут
,
в противном случае пишут
 .
.
Множество можно описать путём перечисления его элементов либо дать правило (свойство) для определения того, принадлежит или нет данный объект рассматриваемому множеству. В первом случае множество обозначается в виде заключённого в фигурные скобки списка элементов. Например,
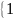 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
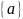 .
.
Если
множество
 задаётся свойствами
задаётся свойствами
 ,…,
,…,
 его
элементов, то пишут
его
элементов, то пишут
=
 ,…,
,…,

и говорят, что есть множество всех элементов, обладающих свойствами ,…, .
Пусть
,
 −
множества. Говорят, что
−
подмножество
множества
(или
содержится в
)
и пишут
−
множества. Говорят, что
−
подмножество
множества
(или
содержится в
)
и пишут
 ,
если каждый элемент множества
является в то же время элементом множества
.
Если
и
,
если каждый элемент множества
является в то же время элементом множества
.
Если
и
 ,
то говорят, что множества
и
равны (или совпадают) и пишут
,
то говорят, что множества
и
равны (или совпадают) и пишут
 .
Пустое
множество
.
Пустое
множество
 не содержит элементов и, по определению,
является подмножеством любого множества.
Если
не содержит элементов и, по определению,
является подмножеством любого множества.
Если
 ∅
и
,
то
−
собственное
подмножество в
.
∅
и
,
то
−
собственное
подмножество в
.
Операции пересечения, объединения и разности множеств и определяются следующим образом:

 ,
,

 ,
,
∖
 .
.
Если пересечение − пустое множество, то говорят, что и непересекающиеся множества. Операции пересечения и объединения удовлетворяют следующим тождествам:
 ,
,
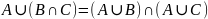 .
.
 .
.
Декартовым произведением множеств и называется множество
 ,
,
 ,
,
 ,
,
где
пары (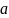 ,
,
 )
являются упорядоченными, т.е.
)
являются упорядоченными, т.е.
 ,
,
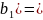 ,
,
 тогда и только тогда, когда
тогда и только тогда, когда
 и
и

 .
Аналогично можно определить декартово
произведение
.
Аналогично можно определить декартово
произведение
 множеств
множеств
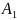 ,…,
,…,
 .
Если
.
Если
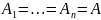 ,
то вместо
,
то вместо
 (
сомножителей) пишут сокращённо
(
сомножителей) пишут сокращённо
 и говорят о
-ой
степени множества
.
Элементами множества
являются всевозможные упорядоченные
наборы (
и говорят о
-ой
степени множества
.
Элементами множества
являются всевозможные упорядоченные
наборы ( ,…,
,…,
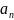 )
длины
,
где
)
длины
,
где
 .
Укажем на следующее различие между
.
Укажем на следующее различие между
 и
и
 для конечных множеств, т.е. содержащих
конечное число элементов:
для конечных множеств, т.е. содержащих
конечное число элементов:
 ,
,
 ,
,
где
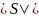 −
число элементов множества
−
число элементов множества
 .
.
Отображения. Понятие отображения − одно из центральных в математике.
Определение.
Отображение
(или функция)
−
это закон (правило), по которому каждому
элементу некоторого множества
ставится в соответствие вполне
определённый элемент заданного множества
 (при этом множества
и
могут совпадать). Это соответствие между
элементами
и
(при этом множества
и
могут совпадать). Это соответствие между
элементами
и
 записывается как
записывается как

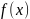 .
Пишут также
.
Пишут также
 или
или
 и говорят, что отображение
и говорят, что отображение
 действует
из
в
.
Множество
называется областью
определения
отображения, а множество
действует
из
в
.
Множество
называется областью
определения
отображения, а множество
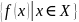 всех элементов
называется областью
значений,
или образом
отображения
и обозначается через Im
(от image
−
англ.) или
всех элементов
называется областью
значений,
или образом
отображения
и обозначается через Im
(от image
−
англ.) или
 .
Множество
.
Множество

называется
прообразом
элемента
.
Более общо, для
 ⊂
положим
⊂
положим

Если
 ,
то
,
то
 .
Множество
.
Множество
 называется
полным
прообразом
множества
.
называется
полным
прообразом
множества
.
Отображение
называется сюръективным,
или отображением
на,
если
 ;
оно называется инъективным,
если
;
оно называется инъективным,
если
 для любых
для любых
 ,
,
 .
Отображение, являющееся одновременно
сюръективным и инъективным, называется
биективным,
или взаимно
однозначным.
.
Отображение, являющееся одновременно
сюръективным и инъективным, называется
биективным,
или взаимно
однозначным.
Равенство
 отображений
и
отображений
и
 означает, что их соответствующие области
совпадают:
,
означает, что их соответствующие области
совпадают:
,
 и
и
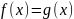 для любого
.
Сопоставление элементу (аргументу)
значения
для любого
.
Сопоставление элементу (аргументу)
значения
 принято изображать ограниченной
стрелкой:
принято изображать ограниченной
стрелкой:
 .
.
Отображение
 обычно называют преобразованием
множества
.
обычно называют преобразованием
множества
.
Отображение
 такое, что
такое, что
 для любого
,
называется единичным,
или тождественным.
для любого
,
называется единичным,
или тождественным.
Произведением
(ещё говорят суперпозицией
или композицией)
отображений
 ,
,
 называется отображение
называется отображение
 ,
определяемое условием:
,
определяемое условием:
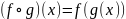 для
любого
.
для
любого
.
Это наглядно изображается треугольной диаграммой:
Далее
вместо
∘
будем просто писать
 .
.
Теорема.
Композиция отображений ассоциативна:
если
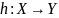 ,
,
 ,
,
 −
три отображения, то
−
три отображения, то
 .
.
Доказательство. Для произвольного имеем
 .
∎
.
∎
Композиция отображений, вообще говоря, некоммутативна.
Некоторые
отображения имеют обратные.
Пусть
,
 −
некоторые отображения. Если
−
некоторые отображения. Если
 ,
то
называется
левым
обратным к
,
а
−
правым
обратным к
.
Если
,
то
называется
левым
обратным к
,
а
−
правым
обратным к
.
Если
 ,
,
 ,
,
то
называется двусторонним
обратным
(или просто обратным)
отображением
для
или к
(а
 обратным отображением для
)
и обозначается через
обратным отображением для
)
и обозначается через
 .
Таким образом,
.
Таким образом,
 ⟺
⟺
 .
.
Утверждение. Если двустороннее обратное отображение к существует, то оно определено однозначно.
Доказательство.
Допустим, что существует ещё одно
отображение
 ,
для которого
,
для которого
 ,
,
 .
Тогда
.
Тогда
 .
.
Другими словами, обратное отображение, если оно существует, определено однозначно. ∎
Лемма. Если , − любые отображения, для которых , то инъективно, а сюръективно.
Доказательство.
Пусть
,
и
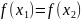 .
Тогда
.
Тогда
 .
.
Значит,
инъективно. Далее, для любого
имеем
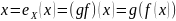 .
Но это означает, что
сюръективно. ∎
.
Но это означает, что
сюръективно. ∎
Теорема. Отображение тогда и только тогда имеет обратное, когда оно взаимно однозначно (биективно).
Доказательство.
Предположим вначале, что
обладает обратным
 .
Из равенств
и леммы
вытекает как сюръективность, так и
инъективность
.
Значит,
биективно. Обратно, пусть
биективно. Тогда для любого
найдётся единственный элемент
такой, что
.
Полагая
.
Из равенств
и леммы
вытекает как сюръективность, так и
инъективность
.
Значит,
биективно. Обратно, пусть
биективно. Тогда для любого
найдётся единственный элемент
такой, что
.
Полагая
 ,
определим отображение
,
обладающее свойствами (1). Значит,
,
определим отображение
,
обладающее свойствами (1). Значит,
 .
∎
.
∎
Теорема. Если отображение биективно, то также биективно, причём

 .
.
Если
отображения
,
 биективны, то их композиция
биективны, то их композиция
 −
также биективное отображение, причём
−
также биективное отображение, причём
 (
( .
.
Доказательство.
По предыдущей теореме из биективности
вытекает существование
,
что равносильно биективности
.
Из условий
,
которые переписываются как
,
,
вытекает равенство
.
Далее, по условию и предыдущей теореме
существуют отображения
 ,
,
 и их композиция
и их композиция
 .
Тогда из равенств
.
Тогда из равенств
 ,
,
(
вытекает равенство . ∎
Теорема.
Если
 конечное множество и отображение
инъективно или сюръективно, то оно
биективно.
конечное множество и отображение
инъективно или сюръективно, то оно
биективно.
Доказательство.
Если
инъективно,
то нужно показать, что
сюръективно, т.е. для каждого
найдётся
 такой, что
такой, что
 .
Положим
.
Положим
 ;
;
 ,
,
 ,
,
 ,
,
…
,
,
…
В
силу конечности
в последовательности
 ,
,
 0, 1, 2, … будут повторения. Пусть
0, 1, 2, … будут повторения. Пусть
 ,
,
 .
Тогда из этого равенства и инъективности
следует равенство
.
Тогда из этого равенства и инъективности
следует равенство
 .
Повторив достаточное число раз сокращение
,
получим
.
Повторив достаточное число раз сокращение
,
получим
 ,
откуда следует, что
при
,
откуда следует, что
при
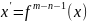 .
.
Обратно,
если
сюръективно,
то нужно показать, что
инъективно.
Если допустить, что
при
 ,
то
число
элементов
в
Im
будет
меньше, чем в
,
что противоречит предположению о
сюръективности
.
Значит,
инъективно. ∎
,
то
число
элементов
в
Im
будет
меньше, чем в
,
что противоречит предположению о
сюръективности
.
Значит,
инъективно. ∎
Понятие
мощности.
Каждому множеству
поставим в соответствие объект
 ,
называемый мощностью
множества
.
Множества
и
имеют одинаковую мощность тогда и только
тогла, когда существует биективное
отображение
.
В этом случае пишут
=
,
называемый мощностью
множества
.
Множества
и
имеют одинаковую мощность тогда и только
тогла, когда существует биективное
отображение
.
В этом случае пишут
=
 .
В частности, пустому множеству
поставим в соответствие в качестве
мощности число 0, а множеству {
,…,
.
В частности, пустому множеству
поставим в соответствие в качестве
мощности число 0, а множеству {
,…,
 },
состоящему из
элементов (
},
состоящему из
элементов ( ,
,…),
−
число
.
Запись
,
,…),
−
число
.
Запись
 означает, что
конечное множество.
Мощности
называют также кардинальными
числами,
или просто кардиналами.
Мощность множества ℕ всех натуральных
чисел принято обозначать
означает, что
конечное множество.
Мощности
называют также кардинальными
числами,
или просто кардиналами.
Мощность множества ℕ всех натуральных
чисел принято обозначать
 (алеф-нуль), а мощность множества
(алеф-нуль), а мощность множества
 всех действительных чисел −
всех действительных чисел −
 .
Множества мощности
называются счётными.
Мощность
.
Множества мощности
называются счётными.
Мощность
 называется также мощностью
континуума.
называется также мощностью
континуума.
