3.7. Равномерное и нормальное распределение на плоскости

Система двух независимых случайных величин (X,Y) имеет равномерное распределение в области D плоскости XOY, если плотность распределения системы в точках плоскости XOY имеет вид:

(3.20)

Система независимых случайных величин (X,Y) имеет нормальное распределение на плоскости, если плотность распределения системы имеет вид:

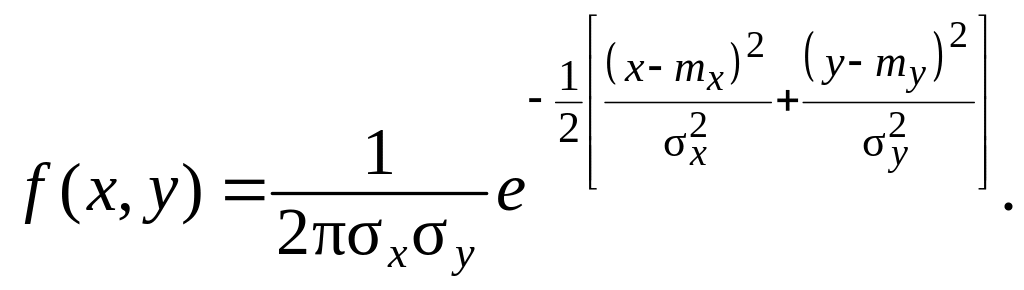(3.21)

Если , то получим каноническую форму нормального распределения на плоскости.

Если , то нормальное распределение независимых случайных величин называется распределением Рэлея, которое распространено в стрельбе, радиофизике, электронике.

Вероятность попадания случайной точки (X,Y) в прямоугольник со сторонами, параллельными осям координат для распределения (3.20), можно вычислить по формуле:

Плотность нормального распределения для системы двух зависимых случайных величин X и Y выражается формулой:

,

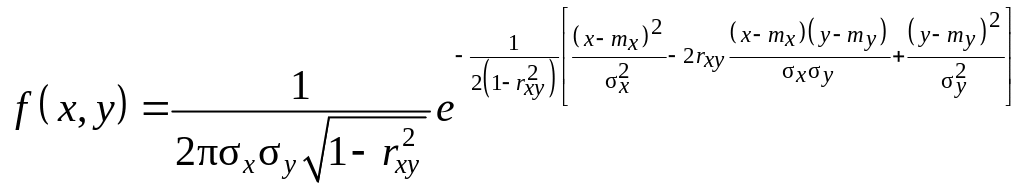т.е. определяется пятью параметрами: , .

Контрольные вопросы

1. Что называется системой случайных величин?

2. Как можно трактовать систему случайных величин?

3. Что называется законом распределения системы двух случайных величин?

4. Дайте определение функции распределения системы двух случайных величин и укажите ее свойства.

5. Дайте определение плотности распределения вероятностей системы двух случайных величин и укажите ее свойства.

6. Что называется условным законом распределения?

7. Как выражается плотность распределения каждой из величин, входящих в систему, через плотность распределения системы?

8. Какие случайные величины называются зависимыми? Независимыми?

9. Что является необходимым и достаточным условием независимости случайных величин?

10. Что называется корреляционным моментом? Коэффициентом корреляции?

11. Чему равен коэффициент корреляции для независимых случайных величин?

12. Какие случайные величины называются некоррелированными?

13. Следует ли из некоррелированности случайных величин их независимость, и наоборот?

14. Как записывается формула для плотности распределения равномерно распределенной в области D системы двух независимых случайных величин?

15. Как записывается формула для плотности распределения нормально распределенной системы двух независимых и зависимых случайных величин?

Глава 4. Функции случайных величин

4.1. Закон распределения функции одной случайной величины

Одной из важных задач в теории вероятностей является определение закона распределения функции одной или нескольких случайных величин, если известны распределения одного или нескольких аргументов. Такие функции тоже являются случайными величинами.

Примерами простейших функций случайных величин являются:

Начнем рассмотрение с наиболее простой задачи о законе распределения функции одного случайного аргумента, т.е.

. (4.1)

Пусть дискретная случайная величина X имеет ряд распределения:

Х	х1	х2	…	х , n
р	p1	p2	…	pn

тогда случайная величина Y будет также дискретной случайной величиной с рядом распределения:

Y	y1	y2	…	y , n
p	p1	p2	…	pn

где

Если все значения различны, то для каждого события { } и { } тождественны, поэтому

.

Если же среди есть одинаковые, то их надо объединить в один столбец, а соответствующие вероятности сложить.

Пример 1. Дана дискретная случайная величина X рядом распределения:

X	1	1	2 .
p	0,2	0,5	0,3

Найти закон распределения случайной величины .

Р е ш е н и е. Возможные значения случайной величины Y:

Ряд распределения случайной величины Y:

Y	1	1	4
p	0,2	0,5	0,3

или

Y	1	2 .
p	0,7	0,3

Пусть теперь случайная величина X является непрерывной случайной величиной с плотностью распределения . Найдем плотность распределения случайной величины, заданной формулой (4.1).

Пусть монотонно возрастающая функция.

Так как монотонная функция, то существует обратное отображение .

Найдем сначала функцию распределения случайной величины Y, т.е. :

.

Дифференцируя полученный интеграл по y, получим плотность распределения случайной величины, заданной по формуле (4.1):

. (4.2)

В случае убывающей функции :

, (4.3)

так как в этом случае .

Объединяя (4.2) и (4.3), получим

. (4.4)

Пример 2. Случайная величина X распределена нормально ( ). Найти закон распределения случайной величины .

Р е ш е н и е. Так как случайная величина X имеет нормальное распределение с параметрами , то ее плотность распределения имеет вид:

.

Функция монотонна на ( ), поэтому можно применить формулу (4.4).

Обратная функция по отношению к функции есть

,

ее производная

.

Следовательно,

.

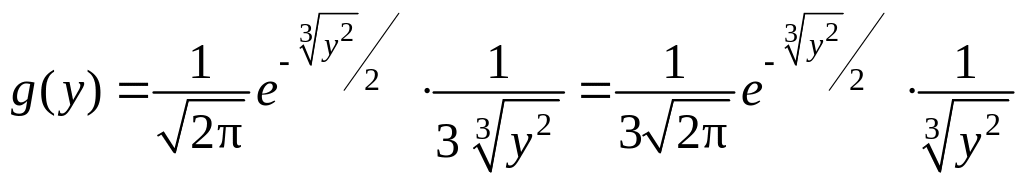Если обратная функция неоднозначная, т.е. одному значению величин Y соответствует несколько значений аргумента , которые обозначим:

где n – число участков, на которых функция (4.1) изменяется монотонно, то формула (4.4) принимает вид:

. (4.5)

Пример 3. Случайная величина X имеет нормальное распределение с параметрами . Найти распределение случайной величины .

Р е ш е н и е. Обратная функция неоднозначная. Одному значению соответствуют два значения функции x:

, .

Применяя формулу (4.5), получим:

.

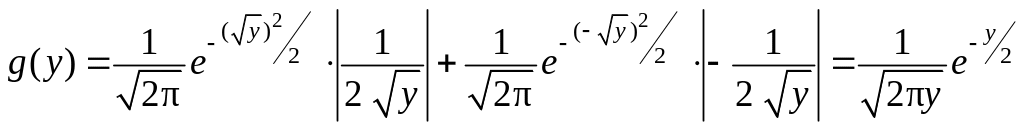Итак,

.

Получили плотность распределения случайной величины Y = X ².