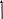Результаты расчетов примера:

Колонну изготовить из уголков 80х8х5,5

Расстояние между планками b = 60 см

Задача 4.2

На стальной стержень ступенчатого переменного сечения с высоты Н падает груз весом Q. Не учитывая собственный вес стержня, определить перемещение сечения I-I после падения груза, а также наибольшее (растягивающее или сжимающее) напряжение в стержне.

Исходные данные: схема 1, A= 19 см² , Н= 0,4 м, а = 0,9 м, b= 0,8 м,

с = 1,35 м, Q = 0,5 кн, Е=210⁴ кН/см²

РЕШЕНИЕ

Пусть  искомое перемещение сечения I-I после падения груза Q,  перемещение того же сечения от статически приложенной силы Q. Тогда

=

где  динамический коэффициент, равный

 определится в виде

= см

=

= = 2,71910^-4  543,397 = 0,1478 см

Наибольшие (сжимающие) напряжения определяются по формуле

=

где - наибольшие (сжимающие) напряжения в стержне от статически приложенной нагрузки Q, равные Q/A:

= кН/см².

ЗАДАЧА 4.3

На шарнирно опертую двутавровую балку падает груз F с высоты h.

Требуется:

1. Найти максимальное нормальное напряжение в балке и указать сечение, в котором оно возникает.

2. Определить перемещения в точке падения груза К₁ и в точке К₂.

Решение

l l l h F K1 K2

Дано: l = 2,7 м,  = 0,55,  = 0,4, F = 7,5 кН, h = 0,04 м Для двутавра № 24a из сортамента А = 37,5 см2, Jx  = 3800 см4, Wx  = 317 см3.

Для нахождения напряжений, перемещений, деформаций при поперечном ударе необходимо прежде всего решит соответствующую статическую задачу

F=7,5 кН RA=7,5 кН z 1,08 м 1,62 м MA = =12,15 кНм 2,7 м x y 7,5 7,5 Qyст кН 12,15 Мхст кНм

Из уравнения статики имеем Строим эпюры внутренних факторов: Определяем максимальное нормальное напряжение

Определение статических прогибов в точках К₁ и К₂ можно осуществлять различными методами. В дальнейшем используем два метода: метод интегрирования дифференциального уравнения упругой линии балки и метод перемножения эпюр (метод Верещагина).

1. Метод интегрирования дифференциального уравнения упругой линии балки EJ_xV =  M_x по участкам.

На втором участке: уравнение имеет вид:

(1)

(2)

- уравнение упругой линии (3)

Определим постоянные интегрирования из условий закрепления балки:

При z = l V = V' = 0, тогда из (2) следует:

кНм²

Из (3) следует:

кНм³

Определим прогиб в т.К₁ при z = l = 1,08 м:

кНм³

см

Определим прогиб в т.К₂ при z = l = 1,485 м:

кНм³

см

Определяем коэффициент динамичности при ударе по соотношению

,

где _ст - есть статический прогиб в точке приложения груза:

_ст = V_K1 = 0,13986 см.

Все величины динамической задачи определяются через решение соответствующей статической задачи и коэффициент динамичности:

кН/см²

2. Метод Верещагина вычисления перемещений при статическом нагружении заключается в перемножении эпюр изгибающих моментов заданного нагружения и единичной силы, приложенной в той точке, в которой требуется вычислить перемещение.

Для вычисления прогиба в точке приложения силы К₁ используем эпюры и от силы F =1, приложенной в той же точке.

F=7,5 кН К1 К2 12,15 3,038 [кНм] F=1 1,62 [м] F=1 1,215 [м] 0,405м 1,62м 1,08м 1,485м 1,215м 2,7м

кНм2 м кНм3 = см

Для вычисления прогиба в точке приложения силы К₂ используем эпюры и от силы F =1, приложенной в той же точке.

м кНм2 кНм3 = см