Вопрос № 2. Многокаскадное радиопередающее устройство с фкм-зондирующим сигналом

Передающее устройство формирует на одной из шести фиксированных частот мощные высокочастотные радиоимпульсы, фазоманипулированные по 13-позиционному коду Баркера. В состав передающего устройства (рис.3.48) входят: блок возбудителя, предварительный широкополосный усилитель (ПШУ), мощный широкополосный усилитель (МШУ), модулятор.

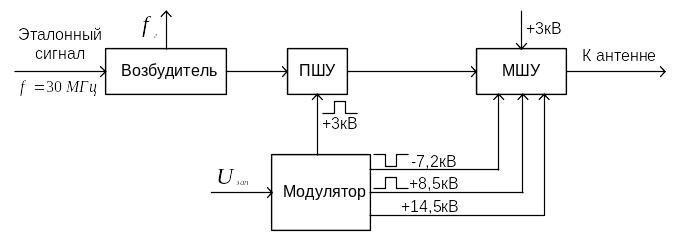
Рис.3.48 Структурная схема передающего устройства РЛС 55Ж6

На вход возбудителя поступает эталонный сигнал, представляющий собой 13-позиционный фазоманипулированный радиоимпульс, сформированный на промежуточной частоте в блоке оптимальной обработки сигнала приемного устройства.

Структура эталонного сигнала и его автокорреляционная функция (при ) представлены на рис.3.49,а,б соответственно.

Рис.3.49 а) Структура ФКМ сигнала; б) Автокорреляционная функция при

Заметим, что на рис.3.49,а знаком «–» (минус) показаны скачки на 180º фазы колебаний при переходе от одного парциального импульса длительностью к другому. Аналогично на 180º изменяется фаза колебаний, если после парциала со знаком («–») следует парциал со знаком («+») (см. рис.3.49,а.).

Блок возбудителя содержит шесть идентичных, независимых друг от друга каналов формирования гетеродинных напряжений на частоте и сигналов передатчика. Гетеродинные непрерывные напряжения частоты формируются кварцевыми генераторами и поступают на смесители возбудителя, на вторые входы которых подаются эталонные сигналы на промежуточной частоте . В результате этого на выходе смесителей формируются сигналы передатчика, частота которых .

Гетеродинные напряжения поступают также на смесители приемника. Сформированные в возбудителе маломощные сигналы передатчика после усиления в ПШУ и МШУ поступают на вход антенны. Предварительный широкополосный усилитель – ламповый, а маломощный широкополосный усилитель на эндотроне представляет собой трехкаскадный усилитель, выполненный в одном корпусе.

Модулятор запускается импульсами запуска от хронизатора РЛС. Он формирует модулирующие импульсы для питания анодных цепей ПШУ (+3кВ) и эндотронов (основного и резервного) (-7,2кВ, +8,5кВ, +14,5кВ).

Сложный ФКМ сигнал записывается в виде:

при ,

где - двузначная ( ) переменная фаза сигнала, манипулированная по заданному коду в моменты времени ;

- длительность парциального импульса (дискрета) фазовой манипуляции; N – дискрет ФКМ сигнала.

Фазокодоманипулированный сигнал обладает следующими достоинствами:

техническая реализация устройств формирования ФКМ-сигнала при сравнительно небольших значениях ( - ширина спектра сигнала) проще, чем для ЛЧМ сигнала;

большие дальность и вероятность обнаружения целей при малом их числе сочетаются со сравнительно хорошим их разрешением по дальности (до нескольких десятков – сотен метров);

сравнительно высокая точность и однозначность одновременного измерения скорости и дальности для одиночной цели по одному импульсу (поскольку ширина спектра ФКМ сигнала , то база сигнала . Автокорреляционная функция одиночного сигнала, фазокодоманипулированного 13-элементным кодом Баркера приведена на рис.3.50,а,б для , и соответственно);

более высокая скрытность, чем у простого и ЛЧМ сигналов с теми же значениями и в виду пониженной спектральной плотности мощности за счет шумоподобности структуры, особенно при большом числе дискретов .

Основные его недостатки:

использование ФКМ сигнала приводит к сложности технической реализации при большом числе дискретов устройств обработки эхо-сигналов и независимо от при устройств формирования сигнала;

равномерный по оси и сравнительно большой уровень (для кодов Баркера - , для рекуррентных M-последовательностей - ) боковых лепестков, что затрудняет селекцию и разрешение по дальности элементов групповой цели.

Рис.3.50 а) Сечение автокорреляционной функции плоскостью и ; б) Сечение автокорреляционной функции плоскостью

Известно, что ФКМ сигнал по коду Баркера имеет максимальное число элементов (дискрет) . В случаях, когда необходимо обеспечить требуемую энергию зондирующего сигнала за счет большой его длительности при сравнительно малой импульсной мощности используют линейные рекуррентные последовательности при фазовой манипуляции или М-последовательности сигналов.

Фазовая манипуляция должна производиться по определенному закону (правилу) в соответствии с некоторой последовательностью цифр: двоичной (цифры ), троичной (цифры ), десятичной (цифры ), в общем случае p-ричной (цифры ).

Каждой цифре можно поставить в соответствие определенный сдвиг фазы . Можно полагать, например, . При этом, если , то возможными фазовыми сдвигами будут 0 и , что эквивалентно умножению на +1 или -1. Если , то манипуляция будет многофазной. Задача получения шумоподобного фазоманипулированного колебания сводится к построению в достаточной мере хаотичной последовательности цифр .

Цифровая последовательность называется рекуррентной, если по любым заданным m последовательным ее элементам можно найти следующий ( )-й элемент, пользуясь одним и тем же правилом, а также ( )-й, ( )-й элементы и т.д. Рекуррентная последовательность называется линейной, если для нахождения какого-либо ее элемента используются линейные операции сложения и умножения предыдущих цифр на постоянную величину. Операции сложения и умножения цифр ведутся по «модулю », чтобы их результат содержал только одну цифру p-ричной системы счисления.

Модульное сложение отличается от обычного следующим. Если при обычном сложении двух цифр получится число, большее , то при модульном из суммы вычитается . Так, например, при сложении цифр 5 и 7 «по модулю 10» получаем 2; при сложении цифр «по модулю 2» получим , но и т.д.

Операция умножения цифр «по модулю » может быть определена как результат повторного сложения одной и той же цифры. Например, при умножении цифр «по модулю 4» ,при умножении цифр 6 и 8 «по модулю 10» получится 8 (последняя цифра числа 48) и т.д. Чтобы отличить модульные операции от обычных, операцию отмечают знаком (mod ). Соотношения, получаемые при модульных операциях, в теории чисел называют сравнениями.

Последовательность цифр, заданная сравнением , является линейной рекуррентной цифровой последовательностью. Получение последовательности может быть осуществлено по схеме (рис.3.51.).

Если на вход линии задержки подать последовательность видеоимпульсов, амплитуды которых соответствуют цифрам , а длительность импульсов соответствует времени задержки между отводами, то в момент времени, когда все импульсы войдут в линию задержки, на выходе сумматора образуется импульс с амплитудой . Подсоединив выход сумматора ко входу линии задержки, можно последовательно получить импульсы с амплитудами , и т.д. Если , то умножение на коэффициент , т.е. на 0 или 1, означает отсутствие или наличие подключения отвода к сумматору.

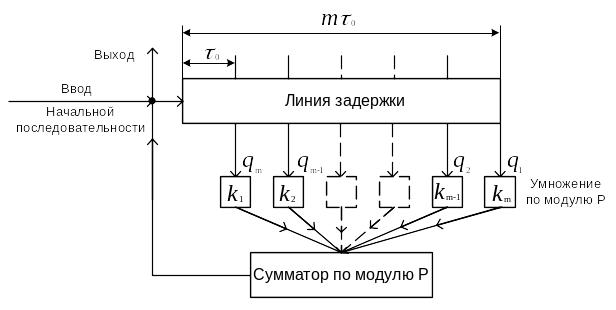
Рис.3.51 Структурная схема генерирования p-ричной рекуррентной последовательности

Поскольку число цифр и отводов ограничено, то в процессе формирования последовательности наступает определенная повторяемость. Так как число возможных вариантов цифр, поступающих на каждый умножитель равно , то число комбинаций этих цифр будет . Из этого числа должна быть исключена чисто нулевая комбинация. Таким образом, максимальная длина неповторяющейся последовательности цифр (максимальный период последовательности) . В частности, при для и т.д. соответственно и т.д.

Максимальная длина последовательности обеспечивается при определенном подборе коэффициентов . Если число элементов последовательности n простое число, то количество различающихся последовательностей максимальной длины выражается наиболее просто и будет . Например, если , , то число – простое, значит .

Значения для последовательностей максимальной длины (М – последовательностей) определяются путем перебора.

Для рассмотренного примера , , коэффициенты выражаются комбинациями 10010, 10111, 11011и зеркальными им комбинациями.

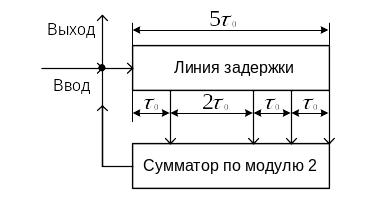
Рис.3.52 Схема генерирования двоичной рекуррентной последовательности ( , , , )

По схеме (рис.3.52.), например, для комбинации коэффициентов нетрудно определить рекуррентную последовательность. Начальная комбинация цифр , , , , может быть произвольной (но не чисто нулевой), поскольку в каждом периоде М – последовательности содержатся все возможные комбинации. Взяв в качестве начальной последовательности , получим , и т.д. Данная рекуррентная последовательность максимальной длины имеет вид

…1111101000100101011000011100110…

Характерно, что число нулей меньше числа единиц на единицу, что является общей особенностью двоичных М-последовательностей.

Подав М-последовательность на фазовый манипулятор 0, , можно осуществить кодирование непрерывного или импульсного сигнала, равносильное умножению его элементов на +1 или -1. Для приведенной в качестве примера последовательности соответствующий период кода сигнала будет

– – – – – + – + + + – + + – + – + – – + + + + – – –+ + – – +.

Отметим еще некоторые особенности М-последовательностей, реализующих их схем и фазоманипулированных ими 0, сигналов.

Ни одна из комбинаций m цифр не может повториться на протяжении n элементов периода последовательности. Неповторяемость структуры можно считать признаком хаотичности, что позволяет использовать такие псевдохаотические последовательности для формирования шумоподобных сигналов.

Все комбинации m цифр перебираются в М – последовательности. Поэтому, возбуждая один и тот же генератор различными начальными комбинациями цифр , будем получать сдвинутые во времени последовательности одинаковой структуры.

Если суммируются начальные элементы двух последовательностей , то в силу линейности должны суммироваться и последующие элементы, т.е. ( )-я цифра будет и т.д. Отсюда следует, что сумма (или, вообще, линейная комбинация) М – последовательностей является также М – последовательностью, но сдвинутой во времени. Это позволяет строить генераторы сдвинутых последовательностей на основе рассмотренного выше генератора одно такой последовательности. Сдвинутые последовательности должны сниматься с дополнительных сумматоров (в отличие от основного не охваченных обратной связью), к которым в различной комбинации подключены отводы линий. Генераторы сдвинутых последовательностей могут использоваться при построении схем корреляционной обработки.

Сечение тела неопределенности сигнала фазоманипулированного М-последовательностью при вдоль оси показано на рис.3.53 для кода .

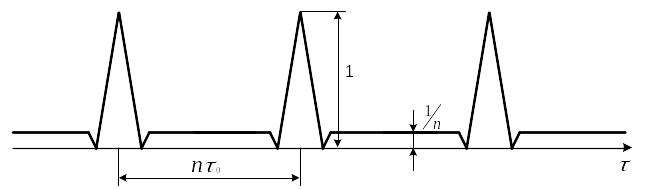Рис.3.53 Сечение нормированной двумерной автокорреляционной

функции сигнала фазоманипулированного М – последовательностью плоскостью

Заметим, что при нулевой расстройке по частоте ( ) уровень боковых остатков имеет постоянную величину, равную . Такой результат дает любая оптимальная обработка сигнала (фильтровая или корреляционная при использовании в качестве опорного напряжения одного или нескольких периодов ожидаемого сигнала).

В РЛС РТВ, предназначенных для обнаружения маловысотных целей, практически реализовано радиопередающее устройство с фазоманипулированным М – последовательностью сигналом с периодом .

Выводы

В ходе проведенного занятия были рассмотрены учебные вопросы занятия (еще раз их озвучить), учебные цели занятия достигнуты.

Задание на самостоятельную подготовку:

1. Изучить и углубить знания материала, рассмотренного на занятии.

2. Отработать в конспекте дополнительный материал по учебным вопросам сегодняшнего группового занятия, изложенный в основной и дополнительной литературе.

Профессор отдела РЛВ РТВ ВВС

подполковник И. Лютиков