2.1. Властивості ймовірностей.

• 0 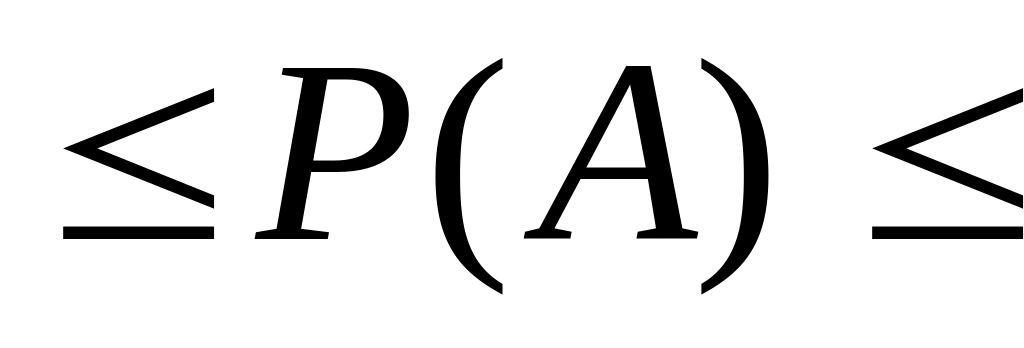1 для кожної випадкової події А.

• Р(А) = 1 для кожної вірогідної події А.

• Р(Ā) = 0 для неможливої події.

• Сума ймовірностей протилежних подій дорівнює 1. Р(А) + Р(Ā) = 1 ; р + q =1.

• Для ймовірності випадкової події Ā, протилежної

випадковій події А, справджується рівність Р(Ā)=1 – Р(А).

2.2. Теореми про додавання.

Якщо випадкові події А , В і С несумісні ( А В С =Ø ), то

Р( А+ В + С) = Р(А) + Р(В) + Р(С).

Ймовірність суми двох будь-яких довільних випадкових подій А і В дорівнює сумі ймовірностей кожної з них без імовірності добутку їх:

Р( А + В ) = Р(А) + Р(В) – Р(АВ ).

2.3. Теореми добутку ймовірностей будь – яких подій.

Тh: Ймовірність добутку двох незалежних подій А і В дорівнює добутку ймовірностей цих подій, тобто Р(А·В) = Р(А) ·Р(В) .

2.4. Залежні події . Умовні ймовірності.

• Означення. Умовні ймовірності Р_А(В) або Р(А/В) визначаються формулою

• Р_А(В) = 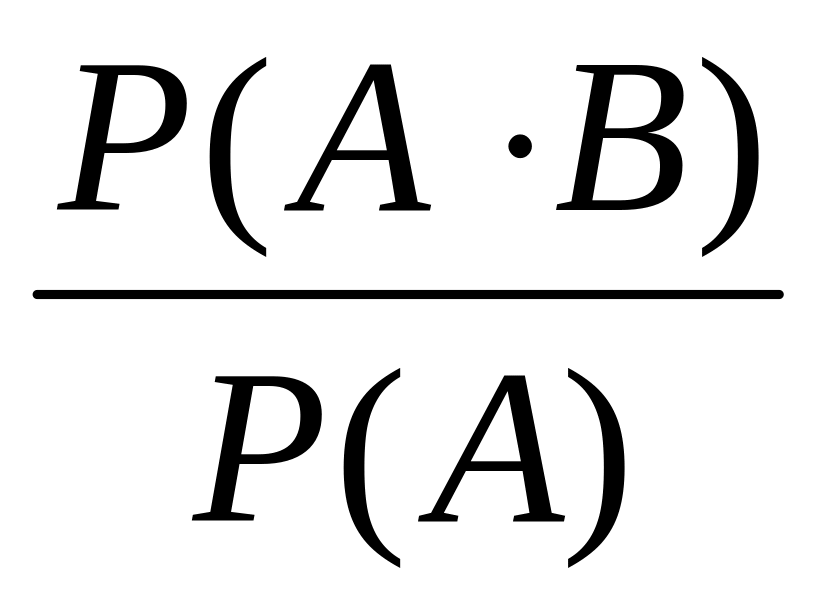, де Р(А) > 0.

Тh: Ймовірність добутку двох залежних подій А і В дорівнює добутку ймовірності однієї з них на умовну ймовірність другої події, якщо перша вже відбулася.

Р(А·В) = Р(А) ·Р_А(В) .

2.5. Незалежні події.

Тh: Ймовірність появи хоча б однієї з подій А₁, А₂, А₃,...,А_n, незалежних у сукупності, дорівнює різниці між одиницею і добутком ймовірностей подій, протилежних даним.

Р(А) = 1 – q₁q₂q₃ ... q _n .

Приклад 1.

Виконується n незалежних дослідів, у кожному з яких подія А з’являється з ймовірністю р . Знайти ймовірність того, що в n дослідах подія А з’явиться хоч би один раз.

Рішення: Нехай подія Е полягає в тому, що подія А з’явиться в n дослідах хоч би один раз, тоді подія означатиме, що подія А в n дослідах не з’явиться жодного разу:

, H( Ē) = (1- h)ⁿ = qⁿ , H(T) = 1 – , H(T) = 1 – (1 – p)ⁿ = 1 – qⁿ

2.6. Формула повної імовірності.

• Означення.

Коли подія А може настати тільки при появі однієї із не сумісних подій

(гіпотез) Н₁,Н₂,...,Н_n, то ймовірність події А знайдемо згідно формули повної імовірності:

Р(А) = . де =1.

Тh: Якщо Н₁, Н₂,...,Н_n – повна група подій і Р(Н_i) > 0 для i = 1;2;…n, то для будь – якої випадкової події А справджується рівність Р(А) = .

Де Р(Н_i) – ймовірність гіпотези Н_i; або Р(А/Н_i) – умовна ймовірність події А при цій гіпотезі.

2.7. Формула ймовірності гіпотез (формула Бейєса).

З формулою повної ймовірності тісно пов’язана формула Бейєса. Якщо до досліду ймовірності гіпотез були Р(Н₁), Р(Н₂), ..., Р(Н_n), а внаслідок досліду подія А відбулася, то можна оцінити ймовірність виконання гіпотези Н_i. Нові, умовні ймовірності гіпотез знаходимо за формулою Бейєса. ( i = 1,2,...,n )

Р_А(Н_i) = .

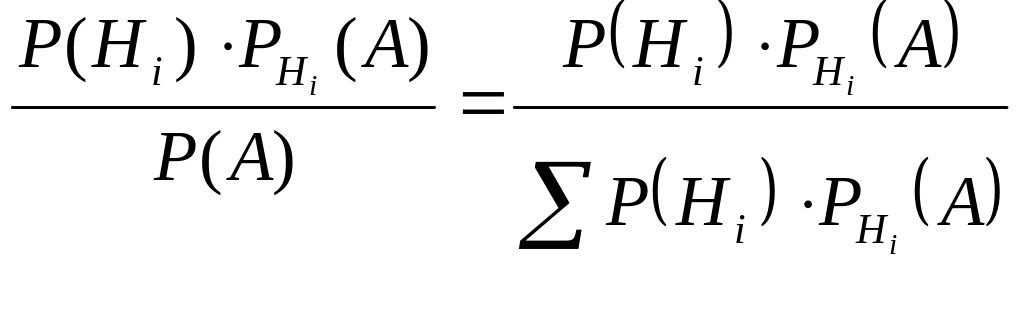Тh: Нехай сукупність випадкових подій Н₁,Н₂,...,Н_n утворює повну групу подій, причому Р(Н_i) > 0, i = 1;2; ... ; n.

Тоді для довільної випадкової події А, такої, що Р(А) > 0, виконується рівність

Р_А(Н_i) = .

Де Р(Н_i) – ймовірність гіпотези Н_i ; – умовна ймовірність події А при цій гіпотезі.

Формула Бейєса дає можливість переглянути ймовірності гіпотез на підставі врахування спостереження результату досліду.

Приклади розв’язання задач до теми № 2.

• Задача № 2.1.

Завод в середньому випускає 27% продукції вищого сорту та 70% першого сорту. Знайти ймовірність того, що навмання взятий виріб буде вищого або першого сорту.

Рішення: Подія А – „навмання взятий виріб – вищого або першого сорту.” Подія А₁ – „навмання взятий виріб – вищого сорту.” Подія А₂ – „навмання взятий виріб – першого сорту”. Р(А) = Р(А₁) + Р(А₂) = 0,27 + 0,7 = 0,97.

• Задача № 2.2.

Із 100 валів з чотирма групами допусків 15 штук мають Ι групу, 40 – ΙΙ групу, 30 штук – ΙΙΙ групу. Визначити ймовірність появи валів четвертої групи.

Рішення: Ймовірність появи вала: Ι групи В₁: Р (В₁) = ; ΙΙ групи В₂: Р (В₂ )= =0,4;

ΙΙΙ групи В₃: Р(В₃) =0,3; ΙY групи В₄ : Р(В₄) = .

Кожний вал належить тільки до певної групи, тобто: В₁ + В₂ +В₃ +В₄ =В_В; Р(В₁) +Р(В₂) + Р(В₃) + Р(В₄) =1; 0,15 + 0,4 + 0,3 + Р(В₄)= 1;

Р(В₄) = 1 – (0,15 + 0,4 + 0,3); Р(В₄)= 0,15.

• Задача № 2.3.

Гральний кубик підкидають двічі. Відомо, що сума очок, які випали при першому та другому підкиданнях, менша за 5 ( подія В ). Яка ймовірність того, що при першому підкиданні випало 1(подія А)?

Рішення: Простір Ω складається з 36 рівно можливих елементарних подій. Випадковими подіями А, В є підмножини:

А ={(1;1),(1;2),(1;3),(1,4);(1;5),(1;6)}. В ={ (1;1),(1;2), (2;1),(1;3),(3;1)}. А В = .

Тому Р(А) = ; Р(В ) = ; Р(А В) = .

• Задача № 2.4.

Станок має двигун та редуктор. Станок виходить зі строю, коли виходять з строю двигун та редуктор. Ймовірність поломки двигуна р₁=0,8 і р₂=0,6 поломки редуктора. Знайти ймовірність того, що станок вийде зі строю.

Рішення: Вихід зі строю станка є сума двох сумісних подій. Подія А– вихід двигуна; подія В– вихід редуктора.

Р(А+В)= Р(А) + Р(В) – Р(АВ) ; Р(А + В ) = р₁+р₂–р₁р₂ ;

Р(А+В) = 0,8 + 0,6 – 0,8*0,6 = 1,4 – 0,48 = 0,92.

• Задача № 2.5.

З урни, в якій міститься 5 куль, серед яких 2 чорні й 3 білі, навмання взято 2. Визначити ймовірність того, що серед взятих куль принаймні ( хоча б ) одна буде білою.

Рішення: Позначимо через А подію, що серед взятих куль принаймні

одна буде білою. Позначимо через подію, яка полягає у тому, що обидві взяті кулі чорні. Число п можливих елементарних подій – це число комбінацій . Оскільки в урні всього дві чорні кулі, то число т елементарних подій, які сприяють події , дорівнює . Тому .

Згідно з властивістю Р(А) + Р(Ā) = 1; Р(А) = 1 – Р(Ā) ; маємо Р(А) = 1 – 0,1= 0,9.

• Задача № 2.6.

Два мисливці стріляють одночасно і незалежно один від одного по дичині. Ймовірності влучень у дичину відповідно дорівнюють 0,7 і 0,8. Знайдіть ймовірність того, що: а) обидві мисливці влучать у дичину ;

б) жодний із мисливців не влучить у ціль; в) лише один із мисливців влучить у дичину ;

г) хоча б один із мисливців влучить у дичину .

Рішення: а) Подія А – перший мисливець влучив у ціль. Ймовірність події А: Р(А)= р₁= 0,7. Подія Е – другий мисливець влучив у ціль. Ймовірність події Е: Р(Е) = р₂ = 0,8; Р(А∙Е) = Р(А)∙ Р(Е) = р₁∙ р₂ ; Р(А∙Е) = 0,7∙ 0,8= 0,56.

б) Подія D – жоден мисливець не влучить у дичину .

Ā – подія протилежна події А. Хай подія Ā – перший мисливець не влучить у дичину. Р(А) + Р(Ā)= 1; р₁ + q₁ = 1; Р(Ā) = 1 – р₁ = q₁ = 0,3.

Подія Ē – другий мисливиць не влучив у ціль. Р(Е) + Р(Ē) = 1; р₂ + q₂ = 1; Р(Ē ) = 1 – Р(Е);

q₂ = 1 – р₂; Не влучили у ціль ні перший, ні другий стрілець. Ймовірність події Р(D) = Р(Ā) ∙ Р(Ē ) = q₁ ∙ q₂ = 0,3 ∙ 0,2 = 0,06.

в) Подія С – лише один із мисливців влучить у дичину. Перший мисливець влучив, другий не влучив у дичину – А ∙ Ē. Перший не влучив, другий влучив у дичину – Ā ∙ Е. Для події С вірогідне перше висловлювання або друге висловлювання.

Р(С ) = Р(А) ∙ Р(Ē ) + Р(Ā)∙ Р(Е ) = р₁∙ q₂ + q₁ ∙ р₂;

Р(С ) = 0,7 ∙ 0,2 + 0,3 ∙ 0,8 = 0,14 + 0,24 = 0,38;

г) Подія U – хоча б один із мисливців влучить у дичину. Подія Ū – жоден із мисливців не влучив у ціль. Р(U) + Р( Ū) = 1; Р(U) = 1 – Р(Ū). Зважаючи на пункт б) подія D дорівнює події Ū. Р(Ū) = Р(D). Звідси Р(U) = 1 – Р(D) = 1 – q₁ · q₂ = 1 – 0,06 = 0,94.

• Задача № 2.7.

В кошику міститься n деталей, з яких m стандартних. Знайти ймовірність того, що серед k вийнятих деталей хоча б одна була стандартною.

Рішення: Подія А – серед вийнятих деталей хоча б одна є стандартною, подія Ā – серед вийнятих деталей немає жодної стандартної.

Події А і Ā протилежні: А + Ā = А_в ; Р(А) = 1 – Р(Ā).

Загальне число способів вибору з n деталей k різних позначимо . Нестандартних деталей є (n – m) , з яких k різних нестандартних деталей можна вибрати способами. Отже, ймовірність появи нестандартної деталі , тоді Р( А ) = 1 – .

• Задача № 2.8.

У ящику лежать деталі 3 сортів : 5 – першого, 4 – другого, 3 – третього. З ящика навмання виймають одну деталь і не повертають в ящик. Знайти ймовірність того, що при першому випробуванні з’явиться деталь першого сорту (подія А), при другому – другого (подія В), при третьому – третього (подія С).

Рішення: Р(А) = . Ймовірність події В за умови, що подія А вже відбулася,

Р_А(В) = . Ймовірність події С за умови, що відбулися події А і В, Р_АВ(С)= . Ймовірність сумісної появи всіх трьох залежних подій Р(АВС) = Р(А) · Р_А (В) · Р_АВ (С) = .

• Задача № 2.9.

З урни, в якій міститься 20 куль, серед яких 8 чорних і 9 білих, навмання виймаються поспіль 3 кулі. Яка ймовірність того, що всі вони чорні?

Рішення: Нехай подія А – перша вийнята куля буде чорна. Р(А) = 8/20. Умовна подія В – друга вийнята куля – чорна. Р_А(В)= 7/19. Умовна подія С–третя вийнята куля буде чорною. Р_АВ(С)= 6/18.

Отже Р ( А В С ) = Р (АВС) = Р (А)Р_А (В) · Р_АВ (С) = = .

• Задача № 2.10.

Хлопчик має 3 білих і 7 блакитних повітряних кульок. Випадково луснула одна кулька, а потім друга. Знайти ймовірність того, що з кульок, які луснули, першою була біла, а другою – блакитна.

Рішення: Нехай подія А – перша куля, що луснула – біла. Р(А)= 3/10. Ймовірність того, що друга з кульок, що луснули, буде блакитною (подія В ), знайдена при умові, що перша – біла, тобто умовна ймовірність дорівнює Р_А (В)= 7/9.

Ймовірність по теоремі множення ймовірностей залежних подій дорівнює

Р(АВ) = Р(А)Р_А (В) = · = .

• Задача № 2.11.

Стрілець вистрілив 4 рази. Влучення чи промах не залежить від номера пострілу. Ймовірність промаху – 0,7 , а влучення – 0,3. Знайти ймовірність подій: а) подія А – три перших постріли – промах, а четвертий – влучення; б) подія Е – два влучення.

Рішення: р = 0,3; q = 0,7. а) Р(А) =qqqр = 0,7*0,7*0,7*0,3 = 0,1029.

б) Можливі варіанти події: (ППВВ), (ВВПП),(ПВПВ), ( ВПВП), (ПВВП), (ВППВ). .

Ймовірності кожного з цих шістьох варіантів однакові:

H(GGDD) = 0?7 · 0?7 · 0?3 · 0?3 = 0?0441$ H(T) = H(DD) = 0?0441· 6 = 0?2646/

• Задача № 2.12.

Для інформування про аварію встановлено три незалежні між собою сигналізатори. Ймовірність того, що під час аварії спрацює перший сигналізатор р₁= 0,95; другий – р₂ = 0,9; третій – р₃ = 0,86. Знайдіть ймовірність того, що під час аварії спрацює принаймні один сигналізатор.

Рішення: Подія А – під час аварії спрацює принаймні один сигналізатор. Протилежна подія Ā – під час аварії не спрацює ні один сигналізатор.

q₁ = 0,05; q₂ = 0,1; q₃ = 0,14.

Р(Ā) = q₁q₂q₃ = 0,05*0,1*0,14 = 0,0007;

Р(А) = 1 – Р(Ā) = 1 – q₁q₂q₃ = 1 – 0,0007 = 0,9993.

• Задача № 2.13.

Ймовірність того, що при одному пострілі стрілець влучить у ціль, дорівнює 0,4. Скільки пострілів має зробити стрілець, щоб з ймовірністю 0,9 уразити ціль ?

Рішення: Нехай подія А полягає в тому, що при n пострілах стрілець уражає ціль, а Ā не уражає. Тоді А + Ā = А_в. Розглянемо подію Ā у вигляді Ā= Ā₁Ā₂... Ā_n , де Ā_i – невлучення в ціль при i – ому пострілі;

p – ймовірність влучення в ціль при одному пострілі; q – ймовірність невлучення в ціль при одному пострілі ( p + q = 1).

Тоді Р(А) = 1 – Р( Ā ) ; Р(Ā ) = qⁿ ; P (A) = 1 – qⁿ .

За умовою ; р = 0,4 , тоді q = 0,6 ;

; ; ; .

• Задача № 2.14.

У 6 ящиках складено деталі 2-х сортів. У перших 3-х по 3 деталі першого сорту і по 7 деталей 2-го сорту; в четвертому ящику – дев’ять деталей 1-го сорту і одна деталь 2-го ; у двох ящиках , що залишилися: по одній деталі 1-го і по дев’ять деталей 2-го сорту. З довільного ящика навмання виймають деталь. Визначити ймовірність того, що ця деталь була другого сорту.

Рішення: Усі ящики можна проділити на три групи та висунути три гіпотези: Н_1, Н_2, Н₃. Гіпотези: Н₁ – виймається деталь з ящика 1-ої групи; Н₂ – виймається деталь з ящика 2-ої групи; Н₃ – виймається деталь з ящика 3-ої групи. Ймовірність того, що виймається деталь з ящика певної групи, буде Р(Н₁) = ; Р(Н₂) = ; Р(Н₃) = .

Події Н₁, Н₂, Н₃ – несумісні і утворюють повну групу. Знайдемо ймовірність появи деталі другого сорту за умови, що здійснилася одна з подій Н₁, Н₂, Н₃ :

Р( А/Н₁ ) = ; Р( А/Н₂) = ; Р(А/Н₃) = .

Повна ймовірність: Р(А) = ·Р(А/Н_і) = = 0,67.

• Задача № 2.15.

Серед N екзаменаційних білетів є m „щасливих”. Два студенти підходять один за одним і навмання беруть білет. В якого студента більша ймовірність взяти „щасливий” білет: у того, хто підійшов першим, чи в того, хто підійшов другим?

Рішення: Нехай А – подія , яка полягає в тому, що другий студент взяв „щасливий” білет. Тут можливі лише 2 припущення: Н₁ – перший студент взяв „щасливий” білет, Н₂ – перший студент не взяв „ щасливий білет”.

Імовірність взяти „щасливий” білет для першого студента дорівнює

Р(Н₁) = . Імовірність другого припущення : Р(Н₂) = . Ці події несумісні, й одна з них обов’язково відбувається. Тому вони утворюють повну групу подій. ;

;

Повна ймовірність: Р(А)= Р(Н₁) +Р(Н₂) ; Р(А)= · + · = .

Отже для другого студента ймовірність взяти “ щасливий” білет теж . Тобто студенти мають рівні можливості взяти “щасливий “ білет.

• Задача № 2.16.

Пластмасові болванки виготовляються на трьох пресах. Перший прес виробляє 50% усіх болванок, 2-й прес – 30% і 3-й прес – 20% усіх болванок. При цьому з болванок 1-го пресу виходить у середньому 0,025 нестандартних болванок, з другого – 0,02, з третього пресу виходить 0,015 нестандартних болванок. Знайти ймовірність того, що навмання взята болванка зі складу була стандартна.

Рішення: Якщо мова йдеться про три преси, то можна висунути три гіпотези: гіпотеза

Н₁ – болванка була виготовлена на першому пресі; Н₂ – болванка виготовлена на другому пресі;

Н₃ – болванка виготовлена на третьому пресі. Ймовірність того, що болванка виготовлена на 1-му пресі Р(Н₁) = 0,5. На другому – Р(Н₂)=0,3. На третьому – Р(Н₃) = 0,2.

Нехай подія А – навмання взята болванка зі складу була стандартна.

Тоді умовна ймовірність того, що взята зі складу стандартна болванка була виготовлена на першому пресі =1– 0,025 = 0,975.

Умовна ймовірність того, що взята зі складу стандартна болванка була виготовлена на другому пресі =1– 0,02 = 0,98; умовна ймовірність того, що взята зі складу стандартна болванка була виготовлена на третьому пресі =1 – 0,015 = 0,985.

Повна ймовірність .

Р(А)=0,5*0,975+0,3*0,98 + 0,2*0,985= 0,4875 + 0,294 + 0,197= 0,9785.

• Задача № 2.17.

В урні є n куль, колір яких нам невідомий. Можлива ( n + 1 ) гіпотеза ( припущення ) про кількість білих куль в урні : Н₀, Н₁, Н₂,...,Н_n , де Н_i – гіпотеза, яка полягає в тому, що в урні рівно i білих куль. З урни навмання взяли одну кулю, й вона виявилася білою. Обчислити ймовірність того, що біла куля вийнята з i-ої урни.

Рішення: Природно припустити, що ці гіпотези рівно можливі : Р(Н₁)=Р(Н₂)=...=Р(Н_n) = . Подія В – навмання взята куля виявилась білою. Очевидно Р_Нi(В) = .

Отже, за формулою Бейєса Р_В(Н _i ) = = = .

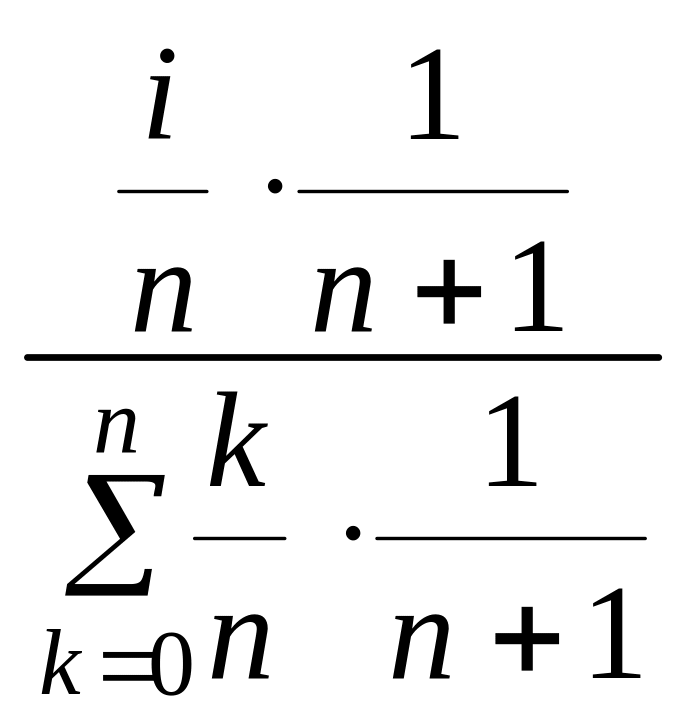Отже, найімовірнішою після досліду є гіпотеза Н_n.

Тема № 3: Повторення випробувань. Схема Бернуллі. Формула Бернуллі. Приблизна формула Пуассона. Локальна та інтегральна теореми Муавра–Лапласа. Найімовірніше число появи випробувань.