2.3 Анализ качества системы в установившемся режиме

Сначала определим такую частоту ₀ тестового гармонического входного сигнала, при которой выходной сигнал УМ имел бы максимальное значение равное 110 В. Сделать это можно через АЧХ, построенной по частотной передаточной функции замкнутой системы по выходу УМ. Так как техническое задание регламентирует амплитуду тестового гармонического входного сигнала равной одному вольту, то на АЧХ необходимо найти такую частоту, при которой модуль частотной передаточной функции будет равен 110. Так как уравнение частотной передаточной функции получится очень громоздким, то всю работу по вычислению частоты «поручим» Mathcad, который может вычислить эту частоту численно без графических построений (Приложение Б.10).

В итоге искомая частота равняется

₀ = 13,316 с^-1.

Определим амплитудные и фазовые искажения (далее АФИ) на частоте ₀, для чего построим ЛАЧХ и ЛФЧХ замкнутой системы. Для построения понадобится передаточная функция (2.7).

На рисунке 2.7 показаны ЛАЧХ и ЛФЧХ замкнутой скорректированной системы из приложения Б.8. По рисунку 2.7 АФИ для гармонического сигнала с угловой частотой ₀ будут равны

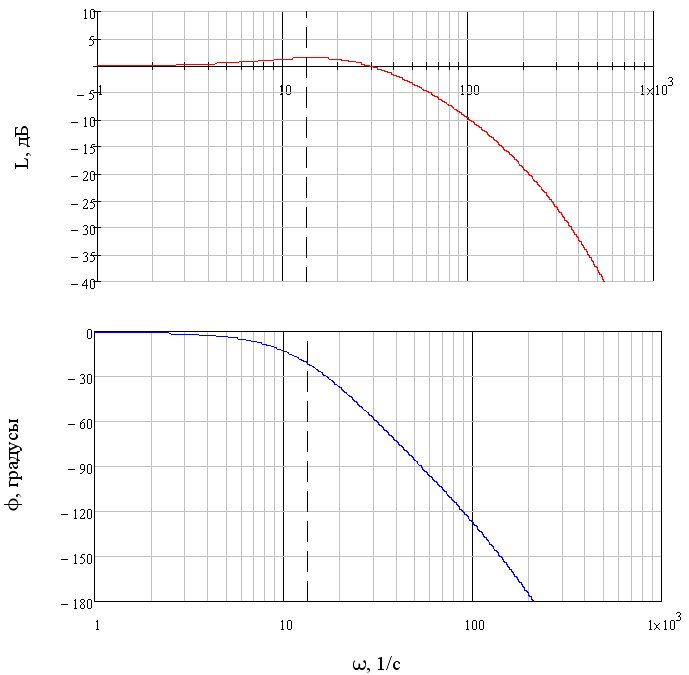
Рисунок 2.7 ЛАЧХ и ЛФЧХ замкнутой системы

Построим расчетные выражения для определения установившейся ошибки слежения при отработке типовых входных сигналов.

Для непериодических сигналов воспользуемся методом коэффициентов ошибок. Непериодическими типовыми сигналами являются постоянный сигнал и линейнонарастающий сигнал. Для определения расчетных выражений в этом случае достаточно первых двух коэффициентов ошибок.

Так как система обладает астатизмом первого порядка, то нулевой коэффициент ошибки равен нулю, а первый можно определить через коэффициент усиления разомкнутой системы

Расчетное выражение для наших типовых негармонических входных сигналов запишется так

(2.9)

Очевидно, что благодаря астатизму системы, ошибка слежения для постоянных сигналов в конечном итоге установится в нуле.

Для сигналов с постоянной скоростью

Как мы видим, благодаря астатизму системы, ошибка слежения сигналов с постоянной скоростью всегда будет постоянной и устанавливаться на уровне .

Так как техническое задание регламентирует скорость тестового сигнала, то этот уровень для него будет

Расчетное выражение ошибки слежения гармонических входных сигналов имеет вид (1.5). Выведем расчетное выражение для тестового гармонического с угловой частотой ₀, для чего воспользуемся передаточной функцией по ошибке слежения

Тогда расчетные выражения для амплитуды и для фазы ошибки слежения примут следующий вид

После расчета в Mathcad, теоретическая ошибка слежения при отработке тестового гармонического входного сигнала примет следующий вид

(2.10)

Представим график на рисунке 2.8 теоретической ошибки слежения (2.10). В разделе 4 мы убедимся, что данное расчетное выражение верно.

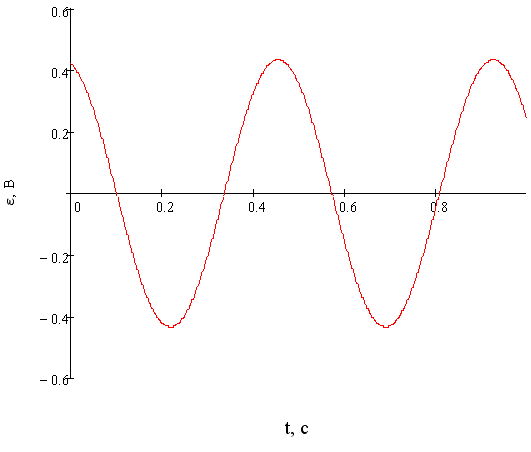
Рисунок 2.8 Установившаяся ошибка слежения при отработке гармонического сигнала с угловой частотой ₀ и единичной амплитудой

3Построение области устойчивости

Построим область устойчивости системы на плоскости параметров «постоянная времени корректирующего устройства – коэффициент усиления разомкнутой системы».

Из постоянных времени корректирующего звена выберем практически значимую T₁. Воспользуемся методикой, предложенной в [4, стр. 125].

Пользуясь (2.6) запишем уравнение, в котором T₁ и k будут переменными

(3.1)

Апериодическая граница устойчивости, определяемая нулевым и бесконечным корнями, вычисляется через следующую систему

Таким образом, апериодическая граница совпадает с осями координат. Колебательную границу устойчивости можно получить, приравнивая предпоследний определитель Гурвица к нулю.

.

Е сли раскрыть определитель и рассмотреть его относительно коэффициента усиления разомкнутой системы, то можно заметить, что получается квадратное алгебраическое уравнение. В этом случае можно представить корни данного уравнения как функцию k(T₁), которая будет определять колебательную границу устойчивости. Таким образом, область устойчивости определяется следующей системой неравенств

(3.2)

Раскрыть определитель проще всего с помощью Mathcad (Приложение Б.9). Ниже на рисунке 3.1 представлена область устойчивости из приложения Б.10.

Рисунок 3.1 Область устойчивости

Заметим, что зависимость параметра T₁ от k практически целиком линейная; лишь при очень малых T₁ зависимость нелинейная (проявляется возле критической частоты ЛФЧХ).

На рисунке 3.1 крестиком отмечено текущее расположение системы в области. По рисунку 3.1 критический коэффициент равен 1546 с^-1, что практически равно расчетному значению таблицы 2.2. Небольшая разница между данными значениями объясняется округлением коэффициентов при расчете.