Глава 3. Основы актуарных расчетов в страховании

3.1 Задача не разорения страховщика

При разумном поведении человек не ставит задачу извлечь выгоду из неблагоприятного случая. Поэтому страховщик, принимая на себя риски страхователя не из альтруизма, а за плату, должен прежде оценить их тяжесть и способы его обеспечения по его удовлетворению, чтобы назначить адекватную им стоимость. Тогда условие не разорения страховщика по виду страхования в каждый момент времени (текущее не разорение) можно записать в виде:

где: – суммарная текущая премия по виду страхования;

- суммарный текущий убыток по виду страхования;

- текущие расходы на ведение дела страховщика, алоцированные на вид страхования;

- текущее приращение страховых резервов по виду страхования.

Если условие не разорения рассматривать за период действия договоров страхования, например, за год, то страховые резервы, по окончанию сроков действия договоров, преобразуются, либо в страховые выплаты (суммарный убыток), либо в доходы страховщика. Тогда условие не разорения можно записать в виде:

Перейдя к равенству и разделив обе части на суммарный убыток, получим известное выражение для расчета минимальной величины страхового тарифа T:

где: - основная часть нетто-тарифа, соответствующая математическому ожиданию суммарного убытка;

- рисковая часть нетто-тарифа, соответствующая возможным отклонениям суммарного убытка в большую сторону относительно его математического ожидания;

- часть тарифа, учитывающая расходы на ведение дела страховщика (нагрузка).

С точки зрения методов расчета тарифов страховые риски можно разделить на три основные группы:

1) опасные события, случайные по времени появления на множестве отдельных однородных распределенных объектов и размеру причиняемых этим объектам, по отдельности, убытков (пожары, аварии, кражи, травмы и т.п.), характерные для массового страхования однородных предметов - домов, автомобилей и т.д.;

2) редкие опасные события, случайные по времени появления и с высоким уровнем убытков, причиняемых сразу множеству компактно расположенных отдельных предметов (катастрофические события);

3) опасные события, о которых известно, что они заведомо произойдут, но неизвестно, в какое время и с кем (утрата трудоспособности по старости, смерть).

Если страховщик имеет дело с массовыми рисками, то, согласно центральной предельной теореме, распределение суммарного по всему страховому портфелю убытка будет подчиняться нормальному распределению независимо от распределения убытков по единичным рискам.

3.2 Расчет тарифа в массовых видах рискового страхования

К рисковым видам страхования, согласно «Методике расчета тарифных ставок по рисковым видам страхования», относятся виды страхования иные, чем страхование жизни, а именно:

• не предусматривающие обязательств страховщика по выплате страховой суммы при окончании срока действия договора страхования;

• не связанные с накоплением страховой суммы в течение срока действия договора страхования.

В свою очередь, из числа рисковых видов страхования выделяют:

• массовые рисковые виды страхования;

• страхование редких событий и крупных рисков;

• медицинское страхование.

Массовые виды страхования охватывают значительное число страхователей и объектов страхования (обычно личное и имущественное страхование, а также страхование ответственности частных лиц и мелких предпринимателей), характеризующихся однородностью рисков, для которых существует достаточно большой объем статистических данных (число объектов страхования не менее нескольких тысяч), позволяющий объективно рассчитать тарифы.

Расчет страхового взноса по рисковому виду страхования включает:

• сбор статистического материала по объектам страхования и произошедшим страховым случаям за прошлый (так называемый расчетный или тарифный) период и проверка его однородности для включения в одну тарифную группу договоров (объектов страхования);

• определение частоты страхового события как частного от деления числа страховых событий (например, числа пожаров) на общее число объектов страхования (например, число застрахованных строений) для тарифной группы;

• определение математического ожидания и среднего квадратического отклонения величины страхового убытка (страховой выплаты) в страховых случаях и средней страховой суммы на один договор страхования для вида страхования (тарифной группы) в соответствии с формулами из любого учебника статистики;

• расчет основной части нетто-взноса;

• расчет рисковой надбавки;

• расчет нетто-взноса как суммы основной части и рисковой надбавки;

• расчет брутто-взноса как суммы нетто-взноса и нагрузки, учитывающей расходы на ведение дела страховой компании, приходящиеся на один договор.

Согласно «Методике расчета тарифных ставок по рисковым видам страхования», утвержденной распоряжением страхового надзора от 08.07.93 № 02-03-36, основная часть нетто-тарифа :

При известной величине и для однородных рисков величина рисковой надбавки определяется по формуле:

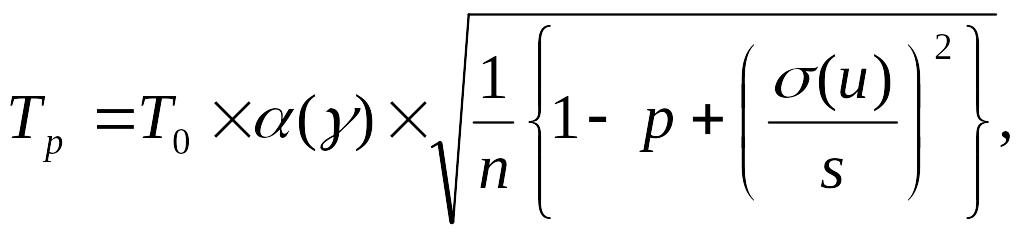
где - коэффициент, зависящий от выбранного значения доверительной вероятности , (табл. 3.1).

Таблица 3.1.

	0,84	0,90	0,95	0,95	0,9986
	1,0	1,3	1,645	2,0	3,0

Если величины и неизвестны, то рисковую надбавку можно приближенно рассчитать по следующей формуле:

При расчетах для нескольких видов страхования рисковая надбавка может быть рассчитана пропорционально моментам распределения случайной функции убытка одним из следующих методов:

• пропорционально математическому ожиданию

• пропорционально среднему квадратическому отклонению:

• пропорционально коэффициенту вариации :

Коэффициент вариации определяется как отношение среднего квадратического отклонения к математическому ожиданию.