ПРИЛОЖЕНИЕ А

Министерство образования и науки

Пензенский государственный университет

Кафедра: «Автономные информационные и управляющие системы»

Курсовая работа по предмету

«Основы алгоритмизации систем управления»

на тему:

«Разработка программы для статистических расчётов»

Выполнил студент: Бахтияров Р.Ж.

группы 08УВ1

Проверил: доцент

Акимова Ю.С.

Пенза 2009

СОДЕРЖАНИЕ

стр.

1 Описание теоретической части

2 Алгоритм основной программы

3 Алгоритмы функций

3.1 Алгоритм функции для построения графика исходного массива

3.2 Алгоритм функции для построения гистограммы и

графика функции Лапласа

4 Текст программы

5 Описание программы

6 Результаты выполнения программы

Выводы

1 Описание теоретической части

Математическая статистика — это раздел математики, посвященный установлению закономерностей случайных явлений или процессов на основании обработки статистических данных —результатов наблюдений или измерений.

Пусть некоторая случайная величина X (например, амплитуда сигнала A) задана значениями x₀, x₁, ... , x_n-1.

Первая задача заключается в оценке неизвестной функции распределения F(x) величины X или ее плотности распределения вероятности f(x), если X — непрерывная случайная величина.

Непрерывной называется случайная величина, которая принимает любые значения из некоторого конечного или бесконечного интервала.

Пусть случайная величина X принимает значения x₀, x₂,...,x_i,..., x_n-1 (рисунок 1). Функция распределения F(x) — это вероятность того, что случайная величина X примет значение меньше некоторого фиксированного действительного числа x_i (рисунок 1). Функция F(x) — это интегральный закон распределения.

Вероятность попадания случайной величины в интервал [x₁, x₂] через функцию распределения можно выразить

P(x₁  X  x₂) = F(x₂) — F(x₁). (1)

Вероятность попадания случайной величины в элементарный интервал x определится

P(x  X  x +x) = F(x +x) — F(x). (2)

Разделим обе части равенства на x и найдем предел при x  0

.

Эта функция есть плотность распределения вероятности или дифференциальный закон распределения (рисунок 1). Функция распределения вероятности через плотность распределения вероятности может быть выражена следующим образом

. (3)

Оценкой плотности распределения вероятности является гистограмма частости.

Рисунок 1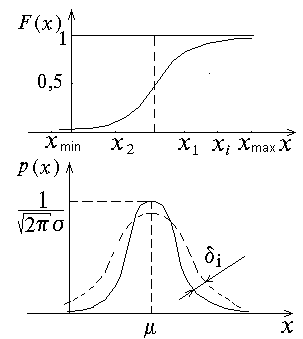

Для ее построения необходимо выполнить следующие действия:

1) центрировать значения случайной величины. Центрированной случайной величиной называется разность между значениями случайной величины и ее математическим ожиданием;

2) упорядочить данные в порядке возрастания значений случайной величины;

3. определить длину интервала по формуле Стерджеса

, (4)

где n — общее количество реализаций случайной величины;

4) область изменения случайной величины разбить на k интервалов. Начало первого и конец последнего вычисляются по формулам:

y₁ = x_min — h/2, y₂ = x_max + h. (5)

5) на каждом участке определить частоту m_i попадания случайной величины X в интервал i = 1,..., k. Частота m_i находится как

Рисунок 2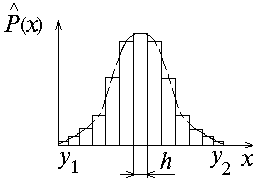

сумма значений случайной величины X, удовлетворяющих условию

y_L < x_j  y_R (6)

где y_L и y_R — левая и правая границы i-го интервала; j = 1,...n;

6) на каждом интервале определить частость m_i/n;

7) построить гистограмму (рисунок 2). Соединив середины прямоугольников, получим кривую, близкую к функции f(x).

Вторая задача математической статистики — это оценка неизвестных параметров.

В этой задаче на основании физических или общетехнических соображений выдвигается гипотеза, что случайная величина X имеет функцию распределения определенного вида, зависящую от нескольких параметров, значения которых неизвестны. По результатам наблюдения случайной величины X нужно оценить значения этих параметров.

Основными параметрами являются моменты первого и второго порядка — это математическое ожидание и дисперсия. Их оценками являются среднее арифметическое и выборочная дисперсия, которые вычисляются по выражениям:

, (7)

. (8)

Третья задача — статистическая проверка гипотез. Задача формулируется следующим образом.

Пусть на основании некоторых соображений можно считать, что функция распределения исследуемой случайной величины X есть F₁(x). Данное предположение называется нулевой гипотезой и обозначается H₀. Как правило, нулевая гипотеза — это предположение о том, что реальный закон распределения не отличается от теоретического. Противоположная гипотеза (есть различия) называется альтернативной и обозначается через H₁.

Если на случайную величину оказывает воздействие пять и более случайных факторов, то закон распределения можно считать нормальным. Для проверки гипотезы о нормальном законе распределения можно воспользоваться критерием Пирсона .

Методика проверки гипотезы заключается в следующем:

1) весь диапазон изменения случайной величины X разбивают на k интервалов и в каждом из них находят частоты m_k (см. п.п.1...5 в первой задаче);

2) оценить среднее арифметическое и выборочную дисперсию (см. вторую задачу);

3) если частоты на крайних интервалах меньше пяти, то интервалы можно объединить в один до m_i  = 5...7 (согласно рекомендациям К. Кокрена;

4. в каждом интервале вычислить функцию Лапласа

 , (9)

где ; y_i — значение случайной величины в середине i-го интервала. Значения функции Ф(t_i) можно найти по таблице 1 [1];

5) определить теоретическую частоту в каждом интервале:

, (10)

6) вычислить расчетную статистику :

. (11)

7) теоретическое значение найти по таблице 7 [1] для  степеней свободы и уровня значимости . Параметр  определяется по формуле  = k — b — 1, где b — количество параметров, оцениваемых по выборке (b = 2). Для статистически незначимых задач  = 0,5;

8) если , то гипотеза о нормальном законе распределения принимается. Говорят, что нулевая гипотеза принимается на уровне значимости 5%.