2 Метод неопределенных коэффициентов.

Этот метод может быть применен для булевых функций от любого числа переменных, однако, для простоты его описания рассмотрим минимизацию функции, зависящей от трех переменных.

Представим функцию в виде следующей ДНФ:

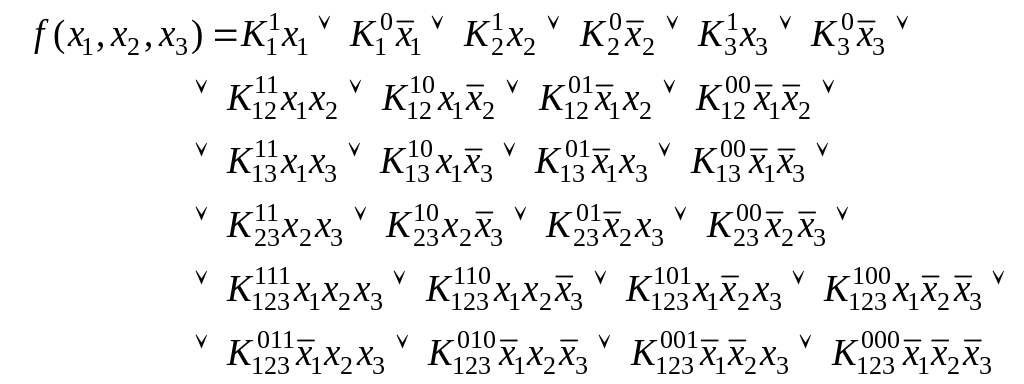
Здесь представлены все возможные конъюнктивные члены, которые могут входить в . Коэффициенты с различными индексами являются неопределенными и подбираются так, чтобы полученная форма была минимальной. Если задать наборы аргументов, подставить в формулу и приравнять полученные выражения (отбрасывая нулевые конъюнкции) значению функции на выбранных наборах, то получим систему уравнений для определения коэффициентов . В общем случае в системе будет уравнений, - число аргументов функции.

(1)

Если функция задана таблицей, то в правой части соответствующих уравнений будут стоять нули и единицы. Для удовлетворения уравнения, в правой части которого стоит нуль, необходимо приравнять нулю все коэффициенты , входящие в это уравнение (это вытекает из определения дизъюнкции).

Рассмотрев все уравнения, в правой части которых стоят нули, и приравняв все коэффициенты этих уравнений нулю, в остальных уравнениях вычеркивают вошедшие в них нулевые коэффициенты. Удобно полученную систему переписать в более сокращенной форме, оставив в ней уравнения, в правой части которых стоят единицы, убрав при этом из этих уравнений нулевые коэффициенты. Затем выбирают в системе самые короткие уравнения. В этих уравнениях приравнивают единице коэффициенты, определяющие конъюнкции наименьшего возможного ранга (это возможно, т.к. дизъюнкция равна единице при обращении в единицу хотя бы одного члена). При этом надо выбрать такие конъюнкции наименьшего ранга, которые чаще встречаются в уравнениях системы. Остальные коэффициенты можно положить равными 0 или 1. Затем рассматривают оставшиеся уравнения и в них выбирают коэффициенты, соответствующие конъюнкциям наименьшего ранга по тому же принципу, и т.д.

Найденные единичные коэффициенты определяют конъюнкции с наименьшим числом знаков, а форма, записанная с этими коэффициентами, определяет минимальную ДНФ данной функции.

Пример 2. Минимизировать функцию (см. пример 1).

Составим систему (обратите внимание на то, что она имеет стандартный вид, лишь в правой части изменяются значения в зависимости от таблицы истинности функции). Для удобства записи системы слева помещают координаты вершин (область определения функции). Верхние индексы коэффициентов комбинируют соответственно из записанных координат вершин с учетом взятых нижних индексов. Например, для второй вершины (0,0,1) верхним индексом для коэффициента будет 00; для - 01 и т.д.

Из уравнений 2, 5, 6 в силу свойств дизъюнкции вытекает, что

Удобно вычеркнуть уравнения, в правой части которых стоят нули, а в остальных уравнениях вычеркнуть коэффициенты равные нулю.

После этого система примет вид:

(2)

В системе (2) в силу свойства дизъюнкции можно приравнять единице коэффициент , тогда 2, 3, 4 и 5 уравнения этой системы превращаются в тождества, из первого же уравнения системы возьмем . Все остальные коэффициенты во всех уравнениях положим равными нулю.

Обратите внимание на тот факт, что единице приравнивают коэффициенты, отвечающие конъюнкциям, содержащим наименьшее число переменных, кроме того, чаще встречающиеся в упрощенной системе уравнений.

Итак, мы нашли , остальные коэффициенты равны нулю. Отсюда минимальная форма данной функции:

Этот метод является громоздким, практически не используется, но мы рассмотрели его здесь с целью обоснования последующих методов.