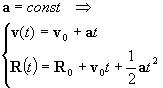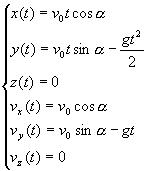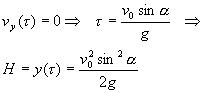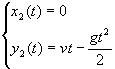3.3. Равноускоренное движение в пространстве

Подобно тому, как это было продемонстрировано в случае движения с постоянной скоростью, формулы одномерного равноускоренного движения обобщаются в векторные соотношения для движения с постоянным ускорением в пространстве (13.20). Приведенные соотношения являются наиболее общими формулами, описывающими все мыслимые случаи равноускоренного движения и его частного случая - движения с постоянной скоростью.

Наиболее часто упоминаемым примером равноускоренного движения в пространстве является движение тела, брошенного под углом к горизонту. Конкретные выражения для зависимостей от времени координат и проекций скорости (13.21) получаются из общих формул равноускоренного движения (13.20).

Время подъема тела определяется из условия обращения в нуль вертикальной составляющей скорости. Подстановка времени подъема в выражение для у-координаты позволяет найти максимальную высоту подъема (13.22).

Время полета тела вычисляется, исходя из условия равенства нулю его у - координаты и оказывается равным удвоенному времени подъема. Т.о. в рассматриваемом случае сохраняется свойство движения тела, брошенного вертикально вверх: время подъема равно времени спуска. Подстановка времени полета в выражение для х - координаты дает значение дальности полета тела (13.23). Максимальная дальность полета достигается при угле бросания в 450.

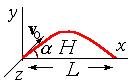
Уравнение траектории получается исключением времени из двух уравнений для x(t) и y(t). Траекторией тела, брошенного под углом к горизонту, является перевернутая парабола (13.24).

	(3.20)	Основные формулы равноускоренного движения.
	(3.21)	Движение тела, брошенного под углом к горизонту
	(3.22)	Вычисление времени подъема и максимальной высоты полета тела, брошенного под углом к горизонту.
	(3.23)	Вычисление времени полета тела и дальности полета.
	(3.24)	Уравнение траектории

Пример 3.3. Расстояние между свободно падающими телами

С высокой башни одновременно бросают с одинаковой по величине начальной скоростью два камня. Одни- вертикально, другой - горизонтально. Каково будет расстояние между камнями через время Т после броска.

Решение

Задачу можно решить двумя способами: "математическим" и "физическим". Первый подразумевает формальную запись координат камней в произвольный момент времени с последующим вычислением расстояния между двумя точками с найденными координатами (13.25 - 13.27). Второй - практически устное решение задачи за счет удачного выбора системы отсчета: с точки зрения свободно падающего наблюдателя оба камня движутся без ускорения.

	(3.24)	Координаты камня, брошенного горизонтально
	(3.25)	Координаты камня, брошенного вертикально.
	(13.27)	Расстояние между камнями.
	(13.28)	В системе отсчета, связанной со свободно падающим наблюдателем оба камня движутся без ускорения, т.е. равномерно и прямолинейно во взаимно перпендикулярных направлениях. Расстояние между ними вычисляется как диагональ квадрата.