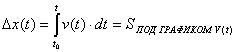2.2. Скорость

Помимо зависимости координаты от времени движение удобно характеризовать скоростью.

Средней скоростью называют отношение изменения координаты ко времени, за которое произошло это изменение (2.2).

Средняя скорость может быть найдена как тангенс угла наклона секущей к графику x(t).

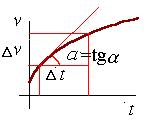
Еще более удобной характеристикой движения является мгновенная скорость, определяемая как средняя скорость за малый промежуток времени (2.3). Мгновенная скорость может быть найдена как тангенс угла наклона касательной к графику x(t).

В случае заданной зависимости координаты от времени скорость для любого момента времени всегда может быть найдена. Соответствующую математическую (вычисление отношения приращения функции к бесконечно малому приращению аргумента) называют дифференцированием, а получающуюся в результате дифференцирования функцию называют производной. В современной физике существуют определенные сомнения по поводу того, может ли реальный (а не выдуманный математиками) интервал времени быть сделан сколь угодно малым. Однако, в классической физике обычно занимаются столь большими отрезками длительностей, что указанные сомнения не существенны.

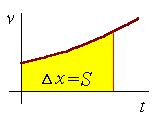
Перемещение (т.е. изменение координаты) тела по заданной зависимости скорости от времени может быть найдено как площадь под графиком v(t). Соответствующая математическая операция носит название вычисления определенного интеграла (2.4). Координата тела в любой момент времени может быть найдена как сумма начальной координаты и перемещения (2.5). Т.о. для нахождения координаты тела в произвольный момент времени по его скорости необходимо знать зависимость скорости от времени и начальную координату.

	(2.2)	Определение средней скорости
	(2.3)	Определение мгновенной скорости.
	Рис.2.1	Геометрический смысл скорости
	(2.4)	Определение перемещения по известной скорости.
	Рис.2.2	Определение перемещение тела по зависимости от времени его скорости.
	(2.5)	Определение координаты тела по его скорости и начальному положению.

2.3. Ускорение

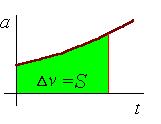
Подобно координате скорость может изменяться во времени. Подобно тому, как вводились средняя и мгновенная скорости, характеризующие скорость изменения координаты, вводятся характеризующие скорость изменения скорости среднее ускорение (отношение изменения скорости к промежутку времени этого изменения) и мгновенное ускорения (отношение изменения скорости к промежутку времени этого изменения при условии малости этого промежутка). Ускорение связано со скорость точно так же, как скорость связана с координатой (2.6 - 2.10).

	(2.6)	Определение среднего ускорения
	(2.7)	Определение мгновенного ускорения.
	Рис.2.3	Геометрический смысл ускорения
	(2.8)	Определение изменения скорости по известному ускорению.
	Рис.2.4	Определение приращения скорости тела по его ускорению
	(2.9)	Определение скорости тела по его ускорению и начальной скорости.