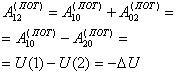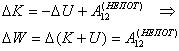8.4. Потенциальная энергия. Механическая энергия. Теорема о изменении механической энергии

Корректное определение потенциальной и механической энергии обычно вызывает серьезные трудности у учащихся на экзаменах. Например, часто встречающееся утверждение о том, что "потенциальная энергия всегда равна mgh" не является правильным, поскольку касается только частного случая потенциальной энергии тела в однородном поле сил тяжести (то есть вблизи поверхности Земли).

Потенциальной энергией тела в заданной точке пространства называется работа потенциальных сил по перемещению этого тела из заданной точки пространства в "начальную" точку, где величина потенциальной энергии принята равной нулю (8.18).

Очевидно, что определенная таким образом потенциальная энергия не зависит от выбора траектории перемещения тела, но зависит от выбора начальной точки. Возникшая неоднозначность не является принципиальной. Во все уравнения физики входит не сама потенциальная энергия, а ее приращение (разность энергий в начальной и конечной точках). Приращение потенциальной энергии не зависит от выбора нулевого уровня.

Используя определение потенциальной энергии (8.18), легко рассчитать ее значения в важных случаях движения тел под действием одних только сил тяжести (8.19) и сил упругости (8.20).

Во многих важных случаях оказывается, что сума кинетической и потенциальной энергии тела не изменяется во времени. Это делает оправданным введение новой величины - полной механической энергии (8.21):

Полной механической энергией тела в данной точке пространства называется сумма его кинетической и потенциальной энергий.

Исходя из теоремы об изменении кинетической энергии, легко получить эквивалентную ей теорему об изменении механической энергии (8.22):

Изменение механической энергии тела равно работе непотенциальных сил.

Для доказательства этой теоремы достаточно воспользоваться теоремой об изменении кинетической энергии (8.9), в которой работы всех сил следует представить в виде суммы работ потенциальных и непотенциальных сил (8.23). Выбрав положение нулевой точки, выделенную работу потенциальных сил можно выразить через изменение потенциальной энергии (8.24). Подстановка полученного результата в выражение для изменения кинетической энергии приводит к требуемому ответу (8.25)

(8.18)

Определение потенциальной энергии тела в точке, характеризуемой радиус-вектором r.

(8.19)

Потенциальная энергия тела на небольшой высоте h над поверхностью Земли (за 0 выбрана энергия на поверхности Земли).

(8.20)

Потенциальная энергия тела, прикрепленного к деформированной на величину Х пружине (за 0 выбрана энергия в положении, соответствующем недеформированной пружине).