Задача 1.1(2) Рассчитать пластовое давление в безводной остановленной скважи­не для следующих условий: L_c=1920 м, h_cт=46 м, ρ_н.д.=878 кг/м³, ρ_н.п.=811 кг/м³

Решение. 1) Так как скважина безводная, то после остановки она заполнена

только нефтью. Рассчитываем высоту столба нефти по формуле:

Скважина эксплуатировалась при забойном давлении большем давления насы­щения.

2) Вычисляем среднюю плотность нефти:

3) Пластовое давление будет равно:

Задача 1.З(3) Определить приведённые давления на отметке ВНК в скважинах 1,2 и 3. Давление замерено в точках А, В, С. Исходные данные: H_ВНК=1300 м, р_А=18,9 МПа, р_B=17,3 МПа, р_С=18 МПа, L_A=1805 м, L_В=1503 м, L_С=1582 м, Ал₁=407 м, Ал₂=277 м, Ал₃=281 м, ρ_н= 0,74 т/м³, ρ_в=1,09 т/м³

Решение: 1) Определим приведенное давление на отметке ВНК (р_BНК) по дан­ным замера давления в т А. Предварительно находим разницу между отметками точки А и ВНК (h_А). Гипсометрическая отметка т.А будет при этом равна:

Из рисунка видим, что:

Так как в интервале между т.А и ВНК пласт насыщен водой, определяем:

2) Определим р_ВНК по данным замера давления в т.В рассуждая аналогич­но, найдём:

Замечая, что между т.В и ВНК пласт насыщен нефтью, определим:

3) Аналогично определим р_ВНК но данным замера давления в т.С.

Таким образом, значения рассчитанных приведенных давлении по всем трем точкам совпали достаточно точно. Определим среднеарифметическое р_ВНК:

Задача 3.2(4). Определить коэффициент открытой пористости образца породы по данным: P_к=25,3 см³, Р_с=23,3 см³ , Р_кк=11,9 см³, ρ_к=0,716 г/см³

Решение. 1) Определяем объём открытых взаимосвязанных пор:

2) Определяем объем образца исследуемой породы:

3) Определяем коэффициент открытой пористости:

или 14,92%

Задача 4.1(5). Определить коэффициент абсолютной проницаемости породы путем пропускания воздуха сквозь образец, если известно:d=3,2 см, l=2,7 см, V_в=3500 см³, t=125 c, μ=0,017 мПА∙с, p_вх=2,1*10⁵ Па, p_вых=1,7*10⁵ Па.

Решение. Коэффициент газопроницаемости породы определяется по формуле:

м²

Задача 4.2(4). Определить подвижность ( ) и коэффициент нефтепроницаемости образца породы (k) по данным лабораторных исследований. Исходные данные: d=4,01 см, l=4,5 см, V=181 см³, t=74 c, μ=7,6 мПа∙с, p_вх=112,4*10⁵ Па, p_вых=111,3*10⁵ Па.

Решение. 1) Коэффициент нефтепроницаемости пород определяется по выражению:

мкм²

где к - коэффициент проницаемости, мкм² ;

Q - расход флюида сквозь породу, см³ /с;

∆р - перепад давления на концах керна при заданном расходе, МПа;

S - плошадь поперечного сечения породы, см²;

μ- коэффициент динамической вязкости флюида, мПа∙c,

2) Подвижность флюида в породе оценивается по выражению:

мкм²/мПа∙с

Задача 4.3(2). Сквозь образец пористой среды происходит фильтрация нефти и воды. Определить относительные проницаемости образца для фильтрующихся жид­костей и водонефтяной фактор, если известны следующие данные:k=2,31 мкм², μ_н=1,71 мПа∙с, μ_в=1,07 мПа∙с, S_в=47%.

Решение* 1) По графику находим, что относительная проницаемость для нефти при S_в=47% равна , для воды

2) Фазовые проницаемости составят:

3) Водонефтяной фактор в про­цессе течения определим из закона Дарси:

Отсюда

Задача 5.1(2). Используя метод полупроницаемых мембран, определим объем вытесненной воды из образца породы при различных значениях капиллярного давления.

Характеристика исследуемого образца и дополнительные исходные данные:m=23,4%, m₀=20,7%, S_уд=611 см²/см³, k=0,471 мкм², L=3,4 см, d=1,5 см.

Оценить минимальную остаточную водонасыщенность и построить кривую распределения пор по их размерам для исследуемого образца.

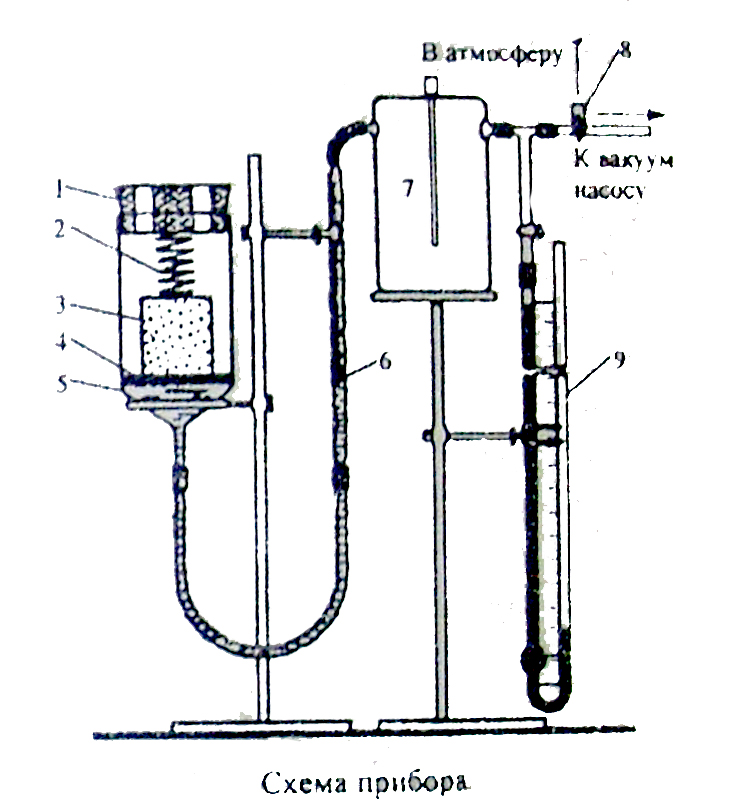
1. Пробка с отверстием для соединения с атмосферой ;

2. Прижимная пружина;

3 Исследуемый образец породы;

4 Мелкопористый фильтр типа Шотта;

5. Стеклянная воронка;

6. Бюретка малого диаметра;

7. Предохранительная склянка, предотвращающая попадание воды в манометр;

8. Трехходовой!!!!

9. Ртутный манометр

№№	Капиллярное давление рк,, мм.рт.ст	Показания Бюретки, см3	Объем вытесненной из образца воды		Объем оставшейся в образце воды		Размеры радиусов пор r, мкм
			см3	% от объема пор	см3	% от объема пор
	1	2	3	4	5	6	7
1	13	4,7	0	0	1,243	100	0
2	23	4,7	0	0	1,243	100	0
3	33	4,65	0,05	4,02032483	1,193	95,9249	29,16771194
4	43	4,625	0,025	2,01016242	1,168	93,9147	22,38452312
5	53	4,55	0,075	6,03048725	1,093	87,8843	18,16102819
6	63	4,45	0,1	8,04064967	0,993	79,8436	15,2783253
7	73	4,25	0,2	16,0812993	0,793	63,7623	13,18540403
8	83	3,95	0,3	24,121949	0,493	39,6404	11,59680113
9	103	3,775	0,175	14,0711369	0,318	25,5692	9,344995087
10	123	3,7	0,075	6,03048725	0,243	19,5387	7,825483691
11	143	3,625	0,075	6,03048725	0,168	13,5082	6,731010448
12	163	3,575	0,05	4,02032483	0,118	9,48796	5,905119595
13	183	3,55	0,025	2,01016242	0,093	7,47780	5,259751333
14	203	3,525	0,025	2,01016242	0,068	5,46764	4,741549232
15	233	3,5	0,025	2,01016242	0,043	3,45747	4,13104933
16	263	3,475	0,025	2,01016242	0,018	1,44731	3,659826973
17	293	3,45	0,025	2,01016242	-0,007	-0,56284	3,285100662
18	333	3,425	0,025	2,01016242	-0,032	-2,57300	2,890493976
19	363	3,415	0,01	0,80406497	-0,042	-3,37707	2,651610176
20	393	3,415	0	0	-0,042	-3,37707	2,449197186

Объем открытых пор:

Заполнение 3 графы таблицы. Количество воды, вытесняемой из образца, получается вычитанием последующего значения из предыдущего (2 графа).

Заполнение 4 графы. Принимая первоначальное количество воды, поглощенной порами образца, равное объему открытых пор (1,243см³) за 100%, подсчитываем процентное содержание воды, соответствующее каждому значению 3 графы.

Заполнение 5 графы. Количество оставшейся в образце воды получается последовательным вычитанием из первоначального количества поглошеиной воды равного 1,243 см³ каждого значения 3 графы.

Заполнение 6 графы. Выводится процентное содержание для каждого значения пятой графы.

Заполнение 7 графы. Радиусы менисков, условно отождествляются с радиусами пор, определяются по формуле Лапласа:

ϭ - поверхностное натяжение воды на границе с воздухом, ϭ =72 дн/см;

ϴ- краевой угол избирательного смачивания, град (16 град);

р_к - капиллярное давление, мм.рт.ст.

Выразим р_к в дн/см² на основании соотношения: I техническая атмосфера 735,6 мм.рт.ст. =981000 дн/см², тогда

По этой формуле подсчитываем радиусы пор и заполняем седьмую графу.

Дальше для построения кривой зависимости между водонасыщенностью и капиллярным давлением необходимо использовать значения первой графы, откладывая их на оси ординат, и значения шестой графы, откладывая их на оси абсцисс.

Для построения кривой, отражающей наглядную иллюстрацию "объемного" участия различного размера пор породы, следует использовать четвертую графу, откладывая значения оси на оси ординат, и седьмую графу, откладывая значения ее на оси абсцисс.

Следует иметь в виду, что на оси абсцисс должны откладываться интервалы размеров "пор", а на оси ординат - объемы воды, соответствующих

данным интервалам размеров освобожденных пор.

Из графика видно, что в данном образце преобладают поры размером радиусов 11,59÷13,15 мкм

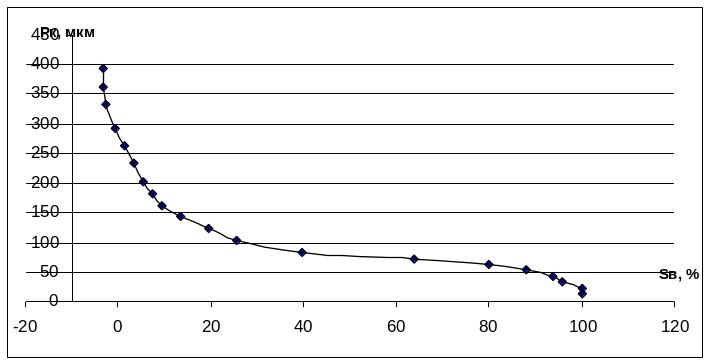
Кривая зависимости между остаточной водонасыщенностью и капиллярным давлением

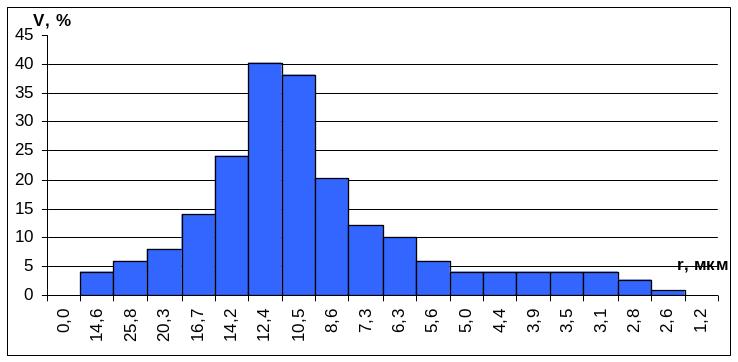
Кривая объёмного участия различного размера пор в породе

Задача 5.2(2). Приняв, что растворимость газа происходит по линейному закону Генри, определить коэффициент растворимости газа α при различных давлениях для условий: V_н=1050 м³, р=22/16 МПа, V_г=21∙10⁴ м³

Решение Согласно линейному закону Генри коэффициент растворимости равен:

С увеличением давления происходит уменьшение коэффициента

растворимости газа.

Задача5.3(2). Определить коэффициенты нефте-, водо- и газонасыщенности породы, если известны следующие данные: V_н=5,13 см³, V_в=3,66 см³, G=89 г, ρ_п=2,4 г/см³, m=0,21, b_н=1,3, b_в=1,07 дол.ед.

Решение. Необходимые коэффициенты определим, пользуясь формулами:

или 65,8%

или 46,9%

или 35,9%

Задача 6.1(4) Определить удельную поверхность неоднородной (по механическому составу) песчаной породы, имеющей следующий фракционный состав:

Фракционный состав породы, мм	Массовое содержание фракций в породе, (мас.%)
0,0024-0,0099	33
0,0099-0,0161	43
0,0161-0,0246	18
0,0246-0,0281	6

Коэффициент открытой пористости песка: m=0,26.

Решение. Удельная поверхность неоднородного по механическому составу песка определяется по формуле:

где d_i - средний диаметр частиц, характеризующие данную фракцию, опреде­ляемый по формуле:

, - ближайшие размеры отверстий сит, характеризующие данную фракцию, см;

- доля веса данной фракции песка, %;

к = 1,2... 1,4 - коэффициент, учитывающий увеличение удельной поверхно­сти за счет нешаровидной формы зёрен (меньшие значения к берутся для окатанных зерен, а большие - для угловатых, значительно отличающихся от зёрен шаровидной формы).

Определим предварительно значения для всех трех фракций:

Для первой фракции:

Для второй фракции:

Для третьей фракции:

Для четвертой фракции:

Задача 6.2(5) Определить удельную поверхность слабосцементированного песчанника, не прибегая к его разрушению для получения механического состава.

Решение, Удельную поверхность в этом случае можно приближённо определить по пористости m и абсолютной проницаемости k породы по рекомендуемой К.Г.Оркиным формуле:

где с₁ - коэффициент, зависящий от разнородности частиц песка; для одинаковых частиц песка с₁₌4330, для осычных нормальных частиц песка с₁=3530.

Для выражения в см²/см³ величина т берется в долях единицы, а k - в мкм².

Требуется определить для образца песчаника, если известны следующие данные: m=0,23 дол.ед., k=2,3 мкм², с₁=3530, S_в=14%.

Имея данные об удельной поверхности породы, можно определить гидрав­лический радиус пористой среды по формуле:

Через значение удельной поверхности можно оценить приближённую вели­чину средней толщины (τ_ср) «плёнки» погребённой (остаточной) воды, предпола­гая равномерное распределение воды по поверхности зёрен (практически такого равномерного распределения не бывает) по формуле:

Задача 7.1(2). Определить количество нефти, которое можно получить из зале­жи за счет упругих свойств среды: внутри контура нефтеносности при падении пластового давления в залежи до давления насыщения. Залежь ограниченная контуром нефтеносности имеет следуй размеры и параметры: F=13,8 км, h=12,4 м, р_пл=17,5 МПа, р_н=8,4 МПа, Т_пл=344 К, m=0,18, s_в=14,5%, β_с=2,8∙10^-4 МПа^-1.

Решение. 1) Определяем коэффициент сжимаемости нефти:

∆р=р_пл-р_н=17,5-8,4=9,1 МПа

b_н и b_пл определяются по графику при Т_пл=344 и р_пл=17,5 МПа, р_н=8,4 МПа.

b_н=1,052 и b_пл=1,037.

Итого имеем:

2) Коэффициент упругоемкости залежи определяется по формуле:

3) Определяем искомый запас нефти, вытесняемый из пласта под дейст­вием упругих сил.

4) Подсчитаем процент нефтеизвлечения от действия свойств среды, предварительно определив общие начальные запасы нефти в залежи.

Процент нефтензвлечения из начального запаса нефти в залежи вследст­вие упругих свойств среды найдем из соотношения:

Задача 8.1(2) По данным лабораторного исследования определить удельную теплоемкость, температуропроводность и теплопроводность образца породы по исходным данным: m=130 г, m₁=240 г, с=350 Дж/кг°С, t₁=13°С, t₂=65°С, t=28°С, ρ_п=2,48∙10³ кг/м³, θ₁=4,7°С, θ₂=3,1°С, L=6,1 см, R=2,6 см.

Решение. 1) Используя уравнение теплового баланса

определим удельную теплоемкость образца:

c = = = 1092,2 Дж/кг· ^oC.