Задания для самостоятельного решения
1. Решить систему уравнений по формулам Крамера и матричным способом.
а)
б)
2. Найти методом Гаусса все решения системы
3. Исследовать систему уравнений с помощью теоремыКронекера-Капелли.
4. Исследовать системы уравнений с помощью теоремы Кронекера-Капелли и решить их.
5. Найти фундаментальную систему решений и общее решение следующих систем:
1.5. Линейные операторы Собственные числа и собственные векторы
Определение. Линейным оператором в линейном n-мерном пространстве называется всякое отображение A: ® , пространства в себя, обладающеесвойствами:
А(λх) = λАх и А(х + у) = Ах + Ау.
Пусть
А - линейный оператор в
и
-некоторый
фиксированный базис. Разложим векторы
,
k = 1, 2, ..., n
по базису B:
Тогда матрица
называется матрицей оператора А в базисе В, причем
(Матрица состоит из вектор-столбцов , k = 1, 2, ..., n.)
Определение.
Пусть число λ и вектор
,таковы,
что Ах = λх.
Тогда число λ называется собственным числом линейного оператора А, а вектор х — собственным вектором этого оператора, соответствующим собственному числу λ.
В линейном n-мерном пространстве это векторное равенство эквивалентно матричному (А - λЕ)Х = 0, X ≠ 0.
Отсюда следует, что число λ есть собственное число оператораA в том и только в том случае, когда det (А - λЕ)= 0, т. е. λ есть корень многочлена
φ (λ) = det (А - λЕ), называемого характеристическим многочленом оператора А. Столбец координат X любого собственного вектора, соответствующего собственному числу λ, есть некоторое ненулевое решение соответствующей однородной системы линейных алгебраических уравнений.
Пример. Вычислить собственные числа и собственные векторы матриц:
Решение:
Составим характеристический многочлен и найдем его корни:
Вычислим
координаты собственных векторов,
соответствующих собственным числам
и 
:
1)
Собственный
вектор 
Собственный
вектор 
-
произвольное постоянное число.
Ответ:
.
Пример.Вычислить собственные числа и собственные векторы матриц:
Решение:Характеристическое уравнение
имееткорни
1)
.
.
Собственный
вектор 
2)
.
-
собственный вектор.
3)
Собственный
вектор 
Ответ:
Задания для самостоятельного решения
1. Найти собственные числа и собственные векторыматриц.
а)
;
б)
2. Комплексные числа
2.1. Алгебраическая форма записи комплексных чисел
Определение. Комплексными числами называются выражения вида
z = х + iy,
где
хи у - произвольные действительные
числа, i - мнимая единица, 
или 
.
Определение.
Два комплексных числа 
и 
называются
равными, если 
и
.
Определение.
Суммой комплексных чисел
и
называется
комплексное число 
.
Определение. Произведением комплексных чисел
и
называется
комплексное число 
.
Определение. Число х называется действительнойчастью комплексного числа z = x + iyи обозначается символом Re z, т. е. х = Re z.
Определение. Число у называется мнимой частью комплексного числа z = х + iy и обозначается символом Im z, т. е. у = Im z.
Определение.
Комплексное число х- iy называетсясопряженным
с комплексным числом z = х + iy и
обозначается
,
причем
.
В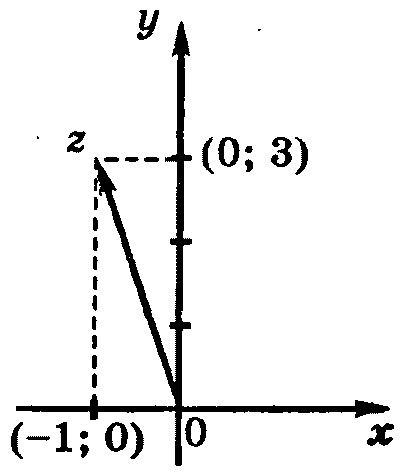
сякое
комплексное число z = x + iy можно изобразить
на плоскости хОу в виде точки М(х; у) с
абсциссой х и ординатой у или
радиус-вектором
.
Справедливо и обратное утверждение.
Пример.Найти значение комплексного числа z и изобразить на комплексной плоскости
.
Решение:
Так
как 
то
Ответ:
-
комплексное число в
алгебраической форме записи.
Пример.
Вычислить 
.
Решение:
Комплексные
числа перемножаются как двучлены, причем
заменяется на -1.
.
Ответ:
.
Пример.
Разделить число 
на
число
.
Решение:Найти
частное 
- это значит представить его в алгебраической
форме. Для этого числитель и знаменатель
дроби надо умножить на число, сопряженное
знаменателю, т. е. на 
Ответ:
-
в алгебраической форме.
Пример. Выполнить операции и представить результат в алгебраической форме:
a)
Решение:
Так
как
,
то 
Ответ:
.
б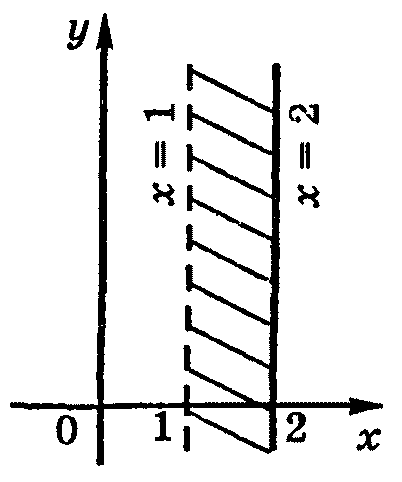
)
.
Решение:
Представим
сначала дробь
в алгебраической форме:
.
Тогда
.
Ответ:
.
Пример. Какие множества точек плоскости задаются условиями:
a) Re z = 2.
Решение:
Т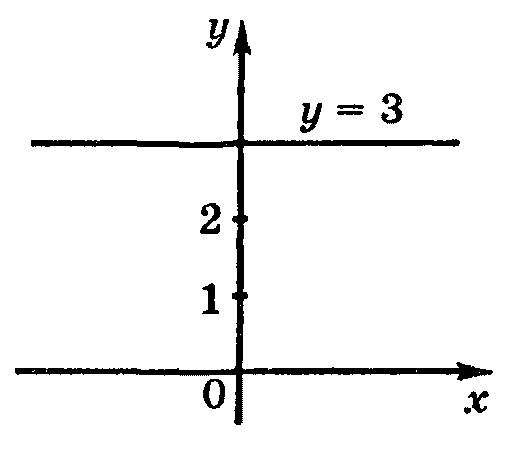
ак
как Re z = x,
то условие Re z = 2 эквивалентно уравнению
х = 2 и задает прямую, параллельную мнимой
оси Оу.
Ответ: Re z = 2 х = 2.
б) 1 <Re z ≤ 2.
Так какRe z = х, то условие 1 <Re z ≤ 2 эквивалентно условию 1 < х ≤ 2. Получаем бесконечную вертикальную полосу между прямыми х = 1 и х = 2, включая и правую прямую х=2.
Ответ:1 < х ≤ 2.
в) Im z = 3.
Решение.
Условие Im z = 3 эквивалентно уравнению у = 3и задает прямую, параллельную действительной оси Ох.
Ответ: прямая у = 3.
Пример.
Вычислить 
и
,
если 
.
Решение.
Так
как 
то
.
Ответ:
.
Пример. Найти действительные решения уравнения
Решение:
Раскроем скобки в уравнении и представим левую часть уравнения в алгебраической форме, х + ix - 2у + 5yi = - 4 + 17i, (x – 2y) + i(x + 5y) =
=-4 + +17i. По определению 2 равенства двух комплексных чисел получаем
- система линейных алгебраических
уравнений относительно
х и у.
Из второго уравнения системы вычтем первое:
7у = 21, у = 3. Из первого уравнения системы получаем х = 2.
Ответ: х = 2, у = 3.
Пример.
Решить уравнение
.
Решение:
сно сопряженные числа
Ответ:
-
комплексно сопряженные числа.